應用PCA-SVM對伺服閥進行故障診斷

王 磊 屈衛東

(上海交通大學電子信息與電氣工程學院，上海 200240)

0 引言

電液伺服閥是將電量轉變成液壓輸出量的電液轉換元件，是電液伺服系統的核心部件。電液伺服閥具有動態響應快、控制精度高和使用壽命長等優點，被廣泛應用于航空、航天、艦船、冶金和化工等領域。但由于電液伺服閥內部結構復雜、精密度高、價格昂貴且工作環境惡劣(高溫高壓)，其發生故障的頻率較高。電液伺服閥性能的好壞將直接影響整個液壓系統的穩定性和控制精度，因此，對電液伺服閥進行故障診斷具有重要的工程意義。

針對某型電液伺服閥，通過調整模型參數模擬故障發生并提取故障數據。故障數據的分類采用支持向量機算法。考慮到原始故障數據的初始維數比較高，為了提高支持向量機的訓練速度和分類速度，采用數據壓縮算法(主元分析法和小波包頻域分析)進行數據的預處理。

故障分類算法的實現形式包括支持向量機(support vector machine，SVM)、主元分析法-支持向量機(principal component analysis-support vector machine，PCA-SVM)和小波包能量特征向量-支持向量機(wavelet packet energy eigenvector-support vector machine，WPEE-SVM)。

1 電液伺服閥建模

1.1 電液伺服閥工作原理

雙噴嘴擋板型電液伺服閥工作原理為［1］:由力矩馬達的通電線圈產生電磁偏轉力矩，使銜鐵擋板組件發生偏轉;擋板的偏轉將引起噴嘴節流口變化，進而導致液流背壓變化并作用到閥芯，引起閥芯移動;閥芯推動反饋桿，反作用于銜鐵擋板，直至反饋力矩和電磁力矩平衡，閥芯停留在某一位置。因此，主閥芯的位移量能精確地隨著電流的大小和方向而變化，從而控制通向液壓執行元件的流量和壓力。

1.2 電液伺服閥的液壓仿真模型

AMESim的全稱為系統工程高級建模和仿真平臺，是法國IMAGINE公司推出的基于鍵合圖的液壓和機械系統仿真及動力學的仿真軟件。AMESim是傳動系統和液壓機械系統建模、仿真及動力學分析軟件，它為用戶提供了一個系統工程設計的完整平臺，可以建立復雜的多學科領域系統的數學模型。

噴嘴擋板可以調用AMESim零件庫中現成的模塊。伺服閥的噴嘴模型可采用AMESim元件庫中的彈簧阻尼元件和位移-流量模塊構成。電液伺服閥的閥體與閥芯采用AMESim元件庫中的流量-位移模塊、壓力-位移模塊、質量模塊和腔體元件組合［2］。

1.3 電液伺服閥的故障模擬

本仿真試驗通過調整液壓模型的參數，模擬仿真了電液伺服閥的6種狀態，即正常狀態、左端限位、右端限位、左側噴嘴阻塞、右側噴嘴阻塞和力矩馬達磁性減弱，具體示意圖如圖1所示。

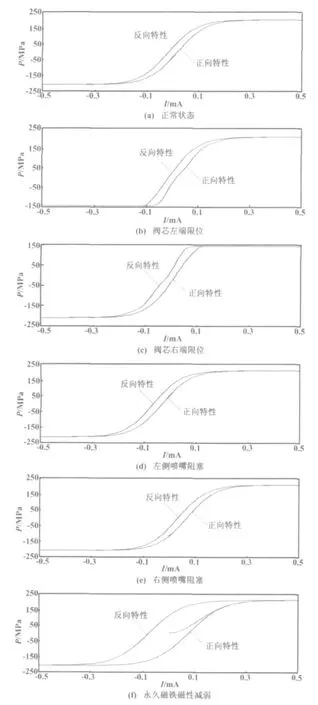
圖1 電液伺服閥的6種狀態Fig.1 Six states of the electro-hydraulic servo valve

電液伺服閥特性曲線包含正向特性曲線和反向特性曲線，兩者并不完全重合，特性曲線具有一定的滯環。

在正常狀態下，電液伺服閥的壓力特性曲線是與輸入電流呈回環狀的函數曲線。當電液伺服閥處于閥芯一端限位狀態時，閥芯運動到限位位置而無法繼續運動，此時壓力維持在某個恒定值。

在噴嘴阻塞狀態下，閥芯的運動特性并不受影響，特性曲線的形狀和正常狀態下的曲線基本一致，只是其特定曲線與正常狀態下的曲線有一個偏移量，其表現就是特性曲線整體左移或者右移。

力矩馬達磁性的減弱，主要是因為磁鐵使用時間太久等原因。這種情況會導致整個的電液伺服閥的反應速度降低，使壓力特性曲線滯環變大、斜率減小［3］。

對于電液伺服閥的6種狀態，分別選取15 MPa、18 MPa、21 MPa、24 MPa和27 MPa作為油壓進行仿真，同時通過設置不同的故障參數模擬多種故障程度，獲取具有代表性的特性曲線。

對仿真得到的壓力特性曲線進行離散采樣，獲取特征故障數據［4］。其中，在正向特性曲線和反向特性曲線各取19個點，即對每個特性曲線采樣38個點作為相應狀態的特征數據。顯然，特征數據為38維，這些特征數據將通過SVM、PCA-SVM和WPEE-SVM這3種分類算法實現分類處理。

2 數據分類處理

2.1 數據壓縮降維

由于原始故障數據維數較高，大大影響了SVM的分類速度，因此，首先對數據進行降維預處理，并在此基礎上采用SVM對數據進行分類。PCA、WPEE主要對特征數據進行降維處理，以提高向量機的訓練速度和分類速度。其中，PCA是常用的線性數據降維算法;WPEE用來提取故障數據的頻域特征信息，從而實現數據壓縮。

2.1.1 主元分析法

PCA是一種線性的數據挖掘算法，用于提取數據主元，以去除噪聲和冗余，實現數據降維［5］。

假設有一組具有m個觀測變量、n個采樣時間點的采樣數據矩陣X1。對X1進行中心歸零化得到X［6］，X的協方差矩陣為CX=XXT。尋找一正交陣P，使Y=PX，且 CY=YYT為對角陣。CY=P(XXT)PTPVΛVTPT(Λ 為對角陣 λ1，λ2，…，λn，V 為正交陣)，所以取 P=VT，則可得 CY=Λ。其中，矩陣CY對角線上第i個元素是X在Pi方向上投影后投影系數的方差。對角線上的元素越大，表明信號越強;反之，則表明可能是存在的噪聲或次要變量。

定義累計誤差貢獻率，當 sum足夠大時，選取P的前K行作為投影矩陣P'，通過P'X可將原有數據降為K維。

2.1.2 小波包分析法

小波包分析能夠為信號提供一種更加精細的分析方法。與小波分析相比，小波包分析不但能夠對信號的低頻部分進行分解，而且也能夠對信號的高頻部分進行進一步的分解。同時，它也能夠根據被分析信號的特征，自適應地選擇相應頻帶，使之與信號頻譜相匹配，從而提高了時間-頻率分辨率［7］。

3層小波包分解原理如圖2所示。

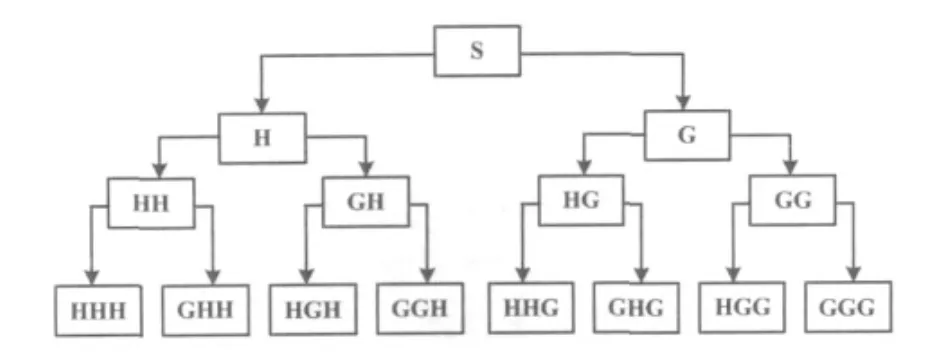
圖2 小波包分解原理圖Fig.2 Principle sketch map of wavelet packet decomposition

圖2中，S代表原信號、H代表低頻、G代表高頻。對于任意給定的信號S，通過一組高低通組合的共軛正交濾波器組G、H，不斷地將信號劃分到不同的頻段上。分解關系如下:S=HHH+GHH+HGH+GGH+HHG+GHG+HGG+GGG。

對信號進行小波包分解的層數視具體信號和對特征參數的要求決定，使用時可采用小波包分解信號的范數表示所在頻帶的信號能量大小。一般來說，在正常運行狀態與故障狀態下，輸出信號的各頻帶成分是不同的，因此可以根據信號能量的大小建立特征向量，用于區分系統不同的狀態［8］。

2.2 支持向量機

故障數據分類是重要的數據挖掘技術，分類的目的就是根據數據集的特點構造一個分類器。分類算法包括決策樹、KNN法、VSM法、貝葉斯法、神經網絡和SVM法［9］。這些算法各有優劣。其中，KNN算法較適用于樣本容量較大的類域的自動分類，對于小樣本容易誤分。VSM算法更適用于文檔分類。貝葉斯方法建立在類別總體概率分布和各類樣本概率密度分布函數的基礎上，難以應用于實際情況。在實際應用中，通常采用神經網絡和SVM法。神經網絡是基于經驗風險最小化原則的學習算法，存在一些固有的缺陷，如神經網絡結構的選擇往往依據經驗。SVM算法建立在統計學基礎上，其分類的效果不受樣本數量的限制，特別適用于小樣本的故障分類。電液伺服閥故障樣本比較少，因而采用SVM作為故障分類算法［10］。

SVM算法建立在統計學原理基礎上，我們可以簡單地將SVM算法理解為對于最優分離超平面的求解。設給定訓練集{(x1，y1)，(x2，y2)，…，(xi，yi)}，其中 xi∈Rn，yi∈{1，-1}，最優分離超平面方程為(wx+b)=0，b 為偏移量。xi代表樣本數據，yi代表樣本數據的分類(如果xi屬于第一類，yi=1;如果xi屬于第二類，則yi=-1)。

設對所有樣本xi滿足以下不等式:

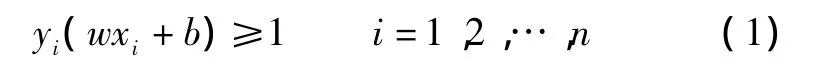
則正反數據間隔d為:

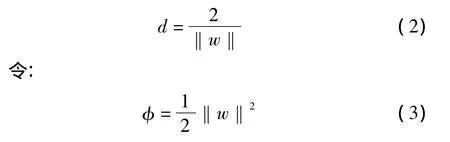
定義如下的Lagrange函數:

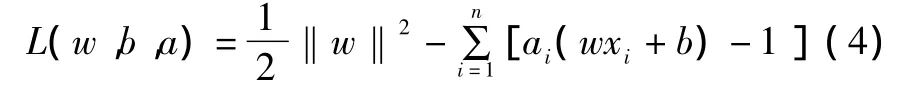
式中:a≥0，為Lagrange乘子。根據已知條件，易證明原問題與其對偶問題是強對偶關系。因而可將上述最優分類面的求解問題轉化為對偶問題。

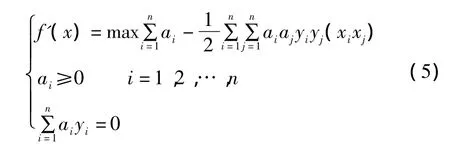
式(5)是一個二次函數的尋優問題，存在唯一解。求解后即可得到分類面函數為:

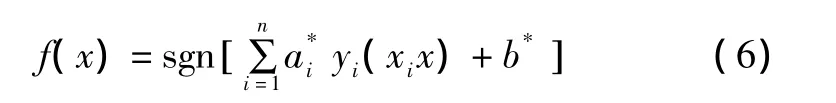
將樣本數據代入式(6)，就可以判定對應樣本所屬的分類。如果原始問題是非線性的，即可通過將原有數據映射到高維空間，進而將原問題轉化為高維空間中的線性問題。映射函數自身很復雜，但Mercer定理證明了內積核函數的存在性。這樣SVM通過核函數K巧妙地實現了高維映射［11］。變換后目標函數和分類函數如下:

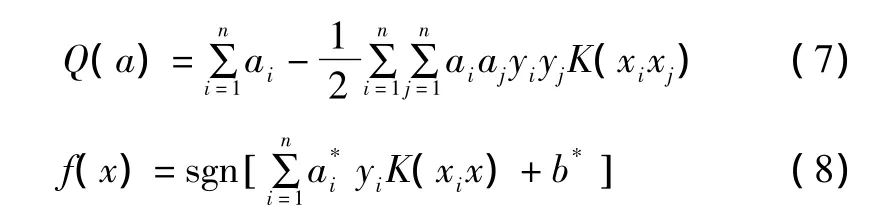
常見的核函數有線性核函數、多項式核函數、RBF核函數和Sigmoid核函數。

3 仿真算法實現

針對前面模型仿真提取的38維特征故障數據，分別采用SVM、PCA-SVM、WPEE-SVM這3種算法進行故障分類，并比較分類結果。

3.1 PCA 數據降維

運用主元分析法對故障樣本數據進行數據降維分析，得到的主元貢獻率如圖3所示。

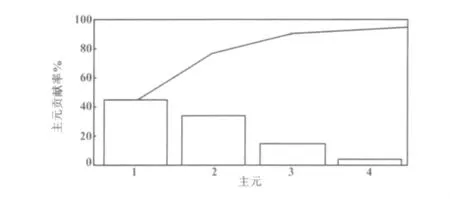
圖3 主元貢獻率Fig.3 Contribution rate of principal component

從圖3可以看出，當取前4個主元時，其貢獻率就可以達到96%以上，完全可以用來表述原有的故障數據。因此，選用前4個主元變量，將原有38維的數據降到4維。

3.2 小波包數據處理

壓力特性曲線具有滯環，為實現對曲線數據的頻域分析，在頻域分析前對原特性曲線進行處理，以去除滯環，形成單條連續波形曲線。其處理方式為:正向特性曲線維持不變，反向特性曲線以電流Ⅰ=0.5 mA為軸作鏡像對稱，可得到原始信號和小波包重構信號的比較曲線。

相關仿真表明，正常狀態和噴嘴阻塞這兩種狀態下各頻段的能量波形分布和能量的幅值存在著明顯差異。因此，可以利用小波包分解提取不同故障狀態下的能量特征向量，以進行故障分類。

小波包能量特征向量的提取實現過程具體如下。

①將信號小波包分解，采用wpdec(Matlab一維小波包的分解函數)。WPEE=wpdec(s1，3，’db1v’，’shannon’);使用db1小波基對x進行3層分解，采用默認的熵標準。

②采用wprcoef函數對分解系數進行重構，提取各頻帶范圍的信號特征。

③采用norm函數求取各頻段信號的總能量(即重構信號離散點幅值矩陣的范數)。

④構造特征向量。將各個頻段能量結合起來組成8維小波能量特征向量，最終將原有數據由38維降至8維。

3.3 算法比較

SVM算法采用LibSVM軟件包，具體實現采用C-SVM。懲罰因子C起到控制學習誤差的作用，C越小，學習誤差越大，訓練時間越長，但訓練得到的SVM具有較強的推廣能力;C越大，學習誤差越小，分類迅速，但訓練得到的SVM推廣能力就弱。多次試驗表明，核函數選取最常用的RBF核函數，C的值選為1。

基于上述參數配置，分別采用SVM、PCA-SVM和WPT-SVM算法對前面模型仿真中提取的38維故障數據進行分類。故障分類結果對照表如表1所示。

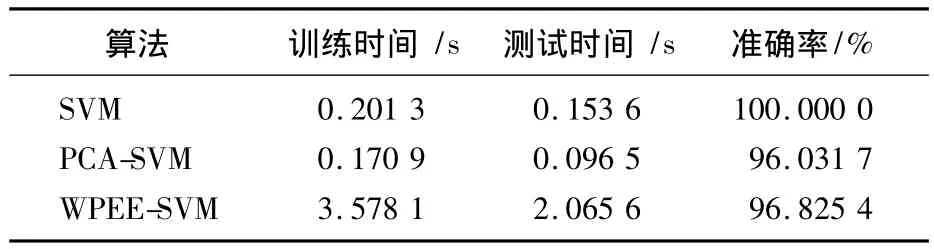
表1 算法結果比較Tab.1 Comparison of the results

從表1可以看出，盡管WPEE-SVM算法可以對原始數據提取頻域特征進行數據的壓縮降維，但由于需要對其進行小波分解等復雜操作，反而大大降低了分類速度和測試速度。經PCA-SVM壓縮后，特征數據的訓練時間和測試時間均有所減少。在對精度要求不高的情況下，顯然應該選擇PCA-SVM算法。

4 結束語

本文討論了某型電液伺服閥故障診斷的算法實現，驗證了算法的可行性。首先利用機理建模建立了對應電液伺服閥的液壓仿真模型，再通過修改模型的參數，完成了故障植入并提取了故障特征信息。隨后分別采用PCA、PCA-SVM和WPEE-PCA算法對故障進行了分類，并驗證了這3種算法的有效性。與SVM相比，PCASVM算法在速度上得到了提高，準確率略有下降;但在大樣本實時系統中，該方法具有較大的優勢。

［1］施康，曾良才.基于AMESim仿真的電液伺服系統故障診斷的研究［D］.武漢:武漢科技大學，2009.

［2］張東，葉志峰.發動機主燃油控制系統建模仿真和試驗驗證［D］.南京:南京航空航天大學，2008.

［3］李成，曾良才.基于B-P神經網絡的電液伺服閥的故障診斷［D］.武漢:武漢科技大學，2010.

［4］曾良才，孫國正.基于特性曲線的電液伺服閥神經網絡的故障模式識別［J］.中國機械工程，2002，10(3):835-838.

［5］肖江，蔣愛憑.基于PCA的SVM故障診斷方法的研究與應用［C］//第十屆全國信息技術化工應用年會論文集，北京:中國化工學會信息技術應用專業委員會，2005:83-86.

［6］Jolliff I T.Principal component analysis［M］.New York:Springer-Velag，1986.

［7］Zhang J Q，Yan Y.A self-validating differential-pressure flow sensor［C］//IEEE Instrumentation and Measurement Technology Conference，Chatham，Kent ME44TB UK，2001:1227-1230.

［8］Daubechies I.Orthonormal bases of compactly supported wavelets［J］.Communication on Pure and Applied Math，1988，41(7):909-996.

［9］Vapnik V N.統計學習理論的本質［M］.張學工，譯.西安:西安電子科技大學出版社，2008:43-57.

［10］Kotsiantis S B.Supervised machine learning:a review of classification techniques［J］.Informatica，2007(31):249-268.

［11］Cristianini N，Shawe-Taylor J.An introduction to support vector machines and other kernel-based learning methods［M］.Beijing:Publishing House of Electronics Industry，2004:15-23.