基于赫茲理論的計算機直接制版設備輥筒模態分析*

胡志煒，孫海達，汪佳敏

(柯達電子(上海)有限公司，上海 201206)

1 引 言

計算機直接制版設備[1]CTP(Computer To Plate)的主要運動是輥筒和絲杠的旋轉。在制版過程中，由于刻版的需求，輥筒旋轉的速度遠遠超過絲杠旋轉的速度。CTP曝光的時間由輥筒的轉速決定。提高輥筒的轉速意味著出版速度的提高，效益的提升。CTP作為印前設備，輥筒上輕微的振動都會影響設備的動態性能導致后續印刷時出現網點擴大、重影、線條抖動、墨色不均等質量問題。盡管在輥筒設計、制造與安裝上進行了眾多的考慮，還有很多理論的問題需要解決，很有必要分析其動態性能。推導赫茲接觸非線性理論并利用Ansysworkbench來對輥筒進行模態分析，研究其振動特性，為后續提高輥筒的旋轉速度提供理論依據。

2 赫茲接觸理論[2]

CTP設備的輥筒兩端采用的是瑞典SKF的深溝球軸承6208ZZ，滾動體和內外圈在不受力的情況下，其接觸為點接觸。在受到外力的作用下，點接觸發生變化過渡至面接觸，處于小變形狀態，同時滾動體和內外圈之間比較光滑，摩擦力遠小于受到的外力，可忽略不計，又因為接觸區域長度遠小于滾動體和內外圈的半徑，所以深溝球軸承中的滾動體和內外圈符合赫茲點接觸理論。

滾動體和內外圈的接觸的幾何條件如圖1所示，兩彈性體相交于空間坐標系O點，并以過點O與滾動體和內外圈的公切平面為x1y1平面，指向滾動體和內外圈內部的坐標軸為z1z12。圖中P1、P2為接觸區域點x1、x2處的作用力。

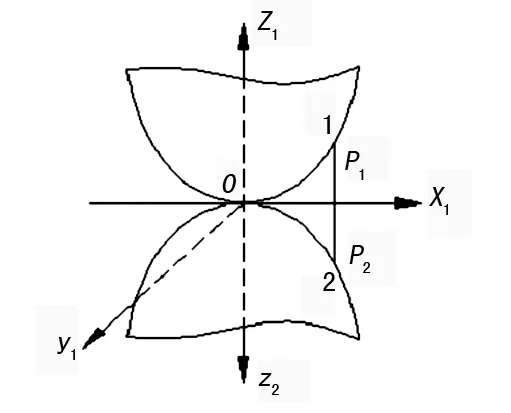
圖1 滾動體和內圈接觸

根據余弦定理可以認為接觸區域點O附近沿Z軸的位移為:

(1)

設點O附近對應x1和y1的滾動體和內外圈表面上對應點為P1和P2，由式(1)可知，其對應x1和y1載荷作用前沿Z軸方向的距離為：

(2)

利用坐標變換，將x1y1乘積項的系數變為0，得到：

z1+z2=A0x2+B0y2

(3)

載荷作用后，點P1和P2沿著Z軸方向的位移為ω1和ω2，由圖1可知：

ω1+ω2=δ-(z1+z2)

=δ-A0x2-B0y2

(4)

式中：δ是兩接觸體的彈性趨近量[3-4]。

根據法向集中力P作用在彈性半空間表面(x′,y′)點，另外一點(x,y)將有法向位移的Boussinesq解：

(5)

式中：E、V是滾動體和內外圈的彈性模量和泊松比。

若p為半空間表面局部區域S上的分布壓力p(x′,y′)時，接觸區域任意(x,y)點的法向位移由Boussinesq解均可表示為:

(6)

若接觸區域S為橢圓，則有:

(7)

壓力p按照半橢球函數進行分布，如圖2所示，可得出：

(8)

式中:a,b分別為橢圓區域S的半長軸與半短軸；P0是橢圓中心處的壓應力。

由式(6)可得分布壓力p(x′,y′)在(x,y)處產生的沿Z軸的法向位移：

(9)

為了積分方便將dx′y′ 表示為r′dr′dθ′，弦長C′D′長度以2l′來表示，如圖3所示。

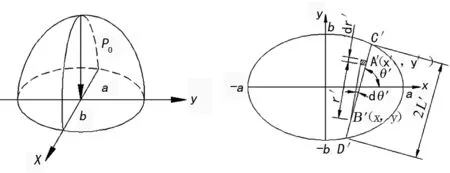
圖2 接觸應力分布 圖3 橢圓區域S的xy平面

將式(9)寫為：

(10)

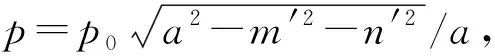
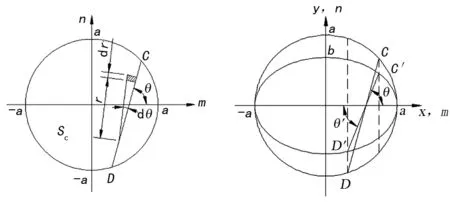
圖4 圓形區域Sc的mn平面 圖5 坐標變換前后比對圖

由圖5可得：

l′cosθ′=lcosθ

(11)

(12)

由式(11)和式(12)可知:

(13)

(14)

(15)

弦長經坐標變化后為:

(16)

為了求出坐標變換前后的關系，需對式(15)兩邊求導

(17)

因此可得出:

(18)

將式(16)和式(17)代入式(10)，可得:

(19)

根據坐標變換關系如圖6所示，可知：

l2=a2-(msinθ+ncosθ)2

(20)

經坐標變換后，p為半球面函數可寫為：

(21)

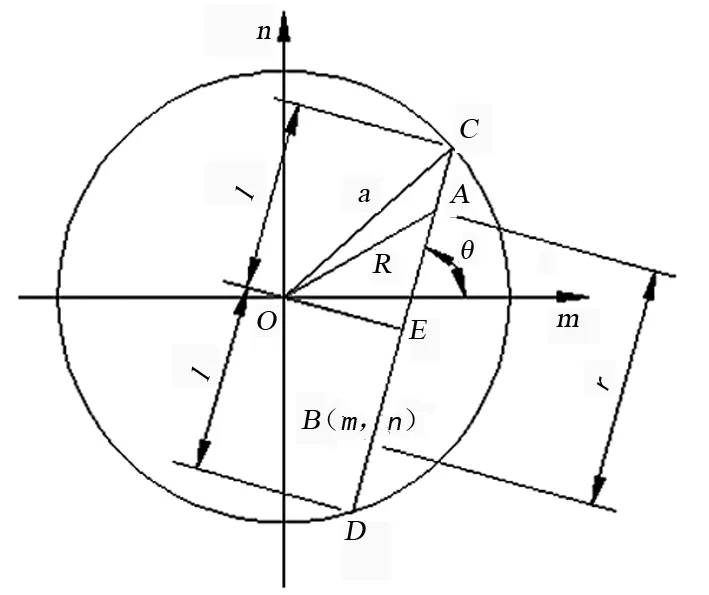
圖6 坐標變換關系圖

于是可得式(19)中的第二項積分為:

(22)

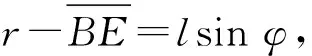
(23)

將式(23)代入式(19)可得:

(24)

將式(14)和式(20)代入式(24)得到:

(25)

令K(e)為第一類橢圓積分[6]:

(26)

L(e)為第二類橢圓積分：

(27)

e為橢圓偏心率：

(28)

對第一類和第二類橢圓積分進行組合，并令:

(29)

B(e)=K(e)-D(e)

(30)

根據式(26)～式(30)，可將式(25)改寫為:

(31)

對變換坐標后的力平衡方程進行積分可得：

(32)

(33)

3 輥筒有限元模態分析[7]

3.1 建模與處理

利用Solidworks2012軟件建立輥筒和深溝球軸承的框架結構圖，然后將模型文件導入Ansysworkbench中劃分網格并定義約束和載荷并指定輥筒和軸承的材料，最后生成有限元動力模型。如圖7所示。

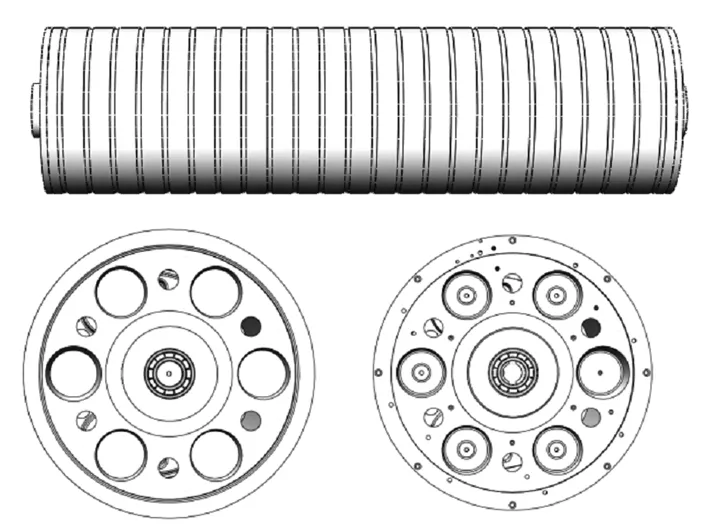
圖7 輥筒和軸承組裝動力學模型

模型在從SolidWorks轉換到Ansysworkbench中為了保證尺寸一致，需要設定單位。定義mm為長度單位，kg為質量單位，N為力單位，s為時間單位。本工程采用的輥筒長為1 708 mm，直徑為459.2 mm，軸承的寬度為18 mm，直徑為80 mm。單位設置完成后，需要設定軸承和輥筒之間的接觸設置，輥筒的內圈和軸承的外圈設為bond方式，軸承滾動體和內彎圈設為光滑無摩擦方式。根據Ansys中規定的面-面接觸選定目標面和接觸面原則，選定滾動體表面作為接觸面，軸承內外圈表面為目標面。

3.2 材料參數

輥筒的材料采用鋁合金6061 T6的材料，其彈性模量為軟件默認的7.1×104MPa，密度為2.77×103kg/m3，泊松比為0.33。軸承的材料采用高碳鉻軸承鋼，彈性模量采用2.0×105MPa，密度采用7.85×103kg/m3，泊松比采用0.3。

3.3 載荷與邊界條件的設置

采用Ansysworkbench軟件設置軸承內圈的6個自由度位移為0，軸承中的滾動體軸向位移為0、徑向位移為自由，x軸方向旋轉自由、Y和Z軸方向的旋轉自由度為0，指定全局坐標系，并劃分網格。共劃分節點數179 960個，單元數量98 598個。載荷、邊界條件和網格劃分如圖8、9所示。

圖8 滾珠和內圈的接觸方式設置 圖9 輥筒和軸承組件的網格劃分

4 運行與分析

通過Ansysworkbench軟件分析自動列出矩陣方程，并計算出輥筒和軸承的位移變化和固有頻率，并可以通過縮放比例來進行查看變形的位置。圖10顯示的是輥筒前6階輥筒和軸承的位移分布云圖和臨界轉速[8-9]的相關振型。

圖10 輥筒和軸承組件前六階模態振型

由于輥筒沒有限制繞x軸旋轉的自由度，所以第一階的固有頻率是剛體運動的固有頻率，從第二階的固有頻率才開始轉化為撓性體運動的固有頻率。采用Ansysworkbench在輥筒恒定轉速為300 r/min時靜力分析結果，輥筒和軸承最大變形量只達到0.005 mm。將其與模態分析中的輥筒在共振時的位移量相比，共振產生的位移量明顯增大。如表1所列。

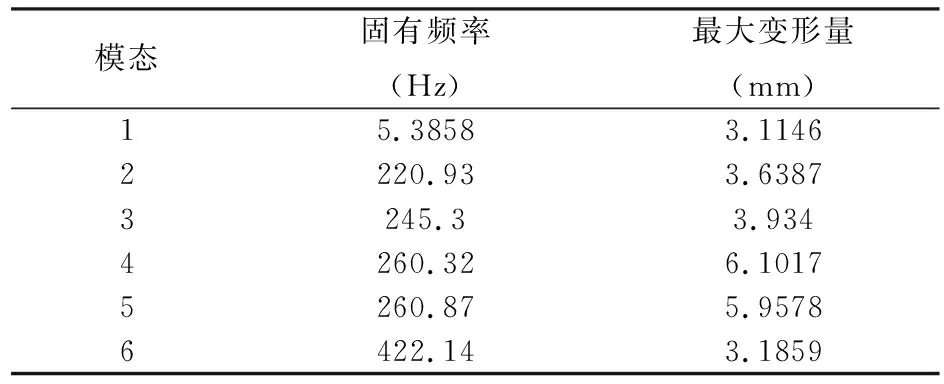
表1 輥筒前六階固有頻率和最大變形量

第一階固有頻率5.3858 Hz轉化為的轉速則是5.3858×60=361 r/min，輥筒在323.15 r/min將發生共振，實際最大工作轉速為270 r/min小于第一階共振頻率滿足需求。若需提高工作轉速增加打版的速度，則輥筒運行接近極限轉速時，需加速運行以最短時間超出，輥筒仍可以正常工作，且不影響出版質量。

5 結 論

通過Solidworks和AnsysWorkbench的聯合仿真，極大化的保證了輥筒的模型與實際模型一致性，避免了結構過度簡化導致的仿真結果不準確。

從模態分析結果可以為設計輥筒的轉速提供了理論和參考依據。利于設計人員更為直觀的熟悉輥筒各階固有特性，為輥筒優化設計提供了依據，同時也為軸承的選型和分析提供了理論和參考。

參考文獻:

[1] 李嘉明.計算機直接(CTP)機的現狀及發展[J].影像技術, 2010(1): 15.

[2] K.L.JOHNSON, Contact mechanics[M].England: Cambridge University Press,1985: 45-83.

[3] 黃琳琳.滾動軸承剛度的非線性分析及工程應用[D].大連：大連理工大學,2009.

[4] [日]岡本純三．球軸承的設計計算[M].北京：機械工業出版社,2003.3.

[5] 羅繼偉，羅天宇.滾動軸承分析計算與應用[M].北京：機械工業出版社,2009.7: 1-14.

[6] 黃琳琳.滾動軸承剛度的非線性分析及工程應用[D].大連:大連理工大學,2009.

[7] 黃穎為，薛鳳梅.印刷機滾筒動態性能的研究[J].包裝工程,2007,28(8):36.

[8] 王軍鋒，孫 康.基于有限元法的轉子臨界轉速計算[J].機械設計,2012,29(12): 12-13.

[9] 陳 喆，王 偉，張仲燾.基于有限元法的滾動軸承接觸總是研究[J].機械，2011(4)：17-20.