雙圓弧齒輪基本參數對齒根彎曲應力的影響*

李金蓮，黃利銀

(長沙航空職業技術學院，湖南 長沙 410014)

1 引 言

雙圓弧齒輪的基本參數不同，所形成的齒廓形狀便不同，從而導致在同等條件下輪齒的承載能力也會不同。因此，對雙圓弧齒輪的基本參數進行研究具有重要意義。但是，目前關于雙圓弧齒輪基本參數對齒根彎曲應力之影響的研究并不完善，絕大多數都只針對幾個影響比較顯著的參數進行了研究分析[1-5]，而極少涉及一些影響不太顯著的基本參數的研究工作。要提高雙圓弧齒輪的承載能力，就不能忽視每一個基本參數的影響。

2 雙圓弧齒輪的齒廓數學模型

任意轉角位置的雙圓弧齒輪齒廓數學模型[6]能準確、真實的描述雙圓弧齒輪齒根過渡曲線上的任一點，筆者基于該數學模型對雙圓弧齒輪齒根彎曲應力進行了一系列的研究，其中文獻[7]將文獻[6]、[8]當中的各段齒廓曲線方程進行了整理，統一為如下公式：

(1)

式中：θ為各段齒廓曲線的漸開線擺角(rad)；Si為各段齒廓曲線上包絡點距刀具中線垂線的距離，Si={Shg，Shf，Shj，Sha}，αi為CT連線與刀具節線的夾角，αi={αgt，αft，αjt，αat}。式中其他參數的意義及計算詳見文獻[6]、[8]。

文獻[9]對齒廓模型的精度進行了數值校驗，在Pro/E環境中將數學模型式(1)生成的齒廓曲線與按范成法加工形成的包絡線進行比較(見圖1)，并測量兩者之間的距離，結果為零，測量誤差小于10-6mm (Pro/E默認精度)，證明所采用的數學模型有足夠的工程精度。

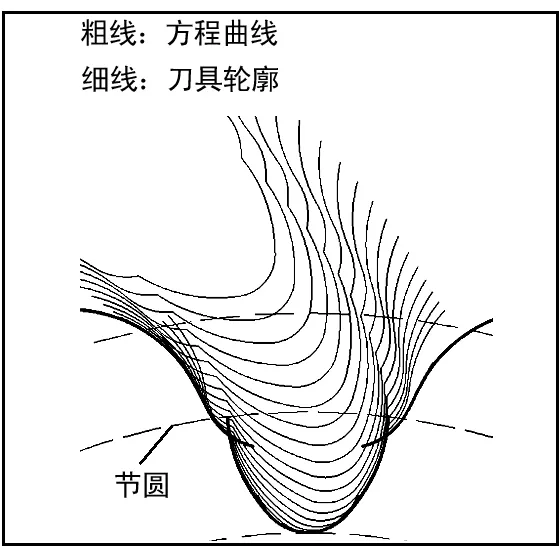
圖1 包絡線-方程曲線

3 雙圓弧齒輪彎曲應力的有限元分析

在Pro/E“關系”中修改參數，構建一個模數m=3，齒數z=16，螺旋角β=18°，齒寬B=10的雙圓弧齒輪模型，利用Pro/E中Mechanica模塊的有限元分析功能，對該模型進行有限元分析。由于計算機容量及速度的限制，僅取齒輪的四個齒作為研究對象。以剛性約束齒輪模型內孔的六個自由度，忽略鍵槽對齒輪應力的影響，將載荷直接以壓力方式加載到輪齒的一側齒面上，載荷大小設為 10 MPa。采用自動劃分網格，使用 Multi-Pass Adaptive(多通道適配方式)，將多項式的最高次數設為9，收斂精度設為5%。最后得到齒輪的有限元分析模型如圖2所示。執行有限元分析后，即可得到該雙圓弧齒輪的彎曲應力云圖(見圖3)。

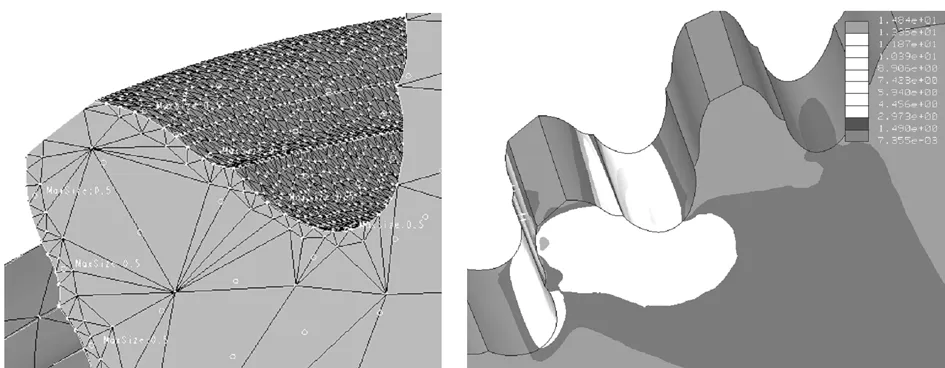
圖2 雙圓弧齒輪有限元分析模型 圖3 雙圓弧齒輪彎曲應力云圖

4 雙圓弧齒輪基本參數對齒根彎曲應力影響

4.1 齒頂高系數對齒根彎曲應力的影響

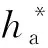
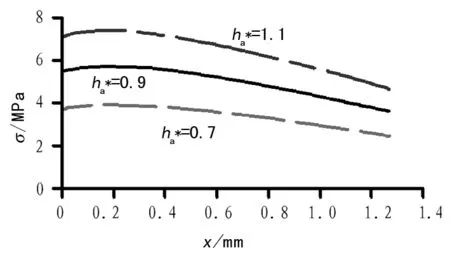
圖4 不同齒根應力沿x軸分布圖

圖5 齒根彎曲應力最大值與的關系

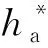
4．2 凹齒齒廓圓弧半徑系數對齒根彎曲應力的影響

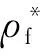
圖6 不同齒根應力沿x軸分布圖

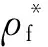
圖7 齒根彎曲應力最大值與的關系

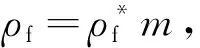
4．3 接觸點到節線距離系數對齒根彎曲應力影響

圖8 不同齒根應力沿x軸分布圖

圖9 齒根彎曲應力最大值與的關系

4．4 系數對齒根彎曲應力的影響

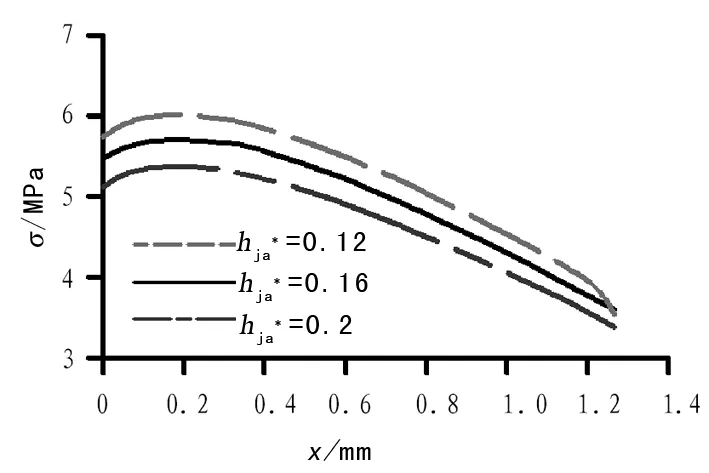
圖10 不同齒根應力沿x軸分布圖

圖11 齒根彎曲應力最大值與的關系

4．5 系數對齒根彎曲應力的影響

圖12 不同齒根應力沿x軸分布圖

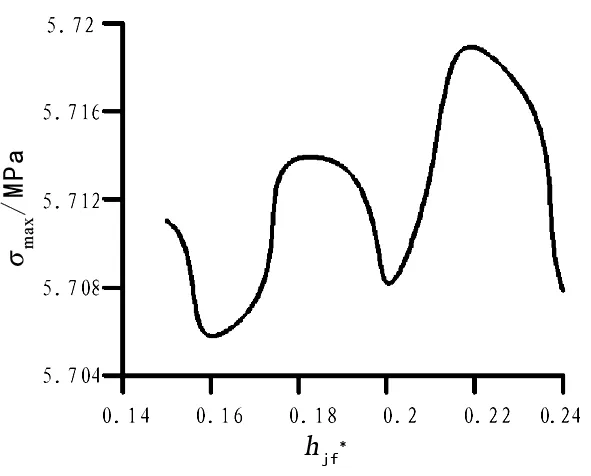
圖13 齒根彎曲應力最大值與的關系

5 結 論

參考文獻：

[1] 武昭暉．雙圓弧齒輪傳動的齒形參數對輪齒彎曲強度影響的研究[D].太原：太原理工大學，2000.

[2] 朱 彤,孟祥戰．全齒高對雙圓弧齒輪彎曲應力的影響[J]．機械設計與制造，2005(10)：47-48．

[3] 吳 潔,蔡春源．基于跑合性能的雙圓弧齒輪齒形參數優化設計[J]．煤礦機械，2001(2)：6-7．

[4] 翟紅升. 硬齒面雙圓弧齒輪齒根的彎曲強度研究[D]．鄭州：機械研究所，2005.

[5] 黃利銀,胡仲勛. 凸、凹齒同時加載雙圓弧齒輪齒根應力分析[J]．機械設計與研究，2010，26(4)：75-78.

[6] 張志強，吳憲平，唐 勇．任意轉角位置的雙圓弧齒輪的齒廓數學模型[J]．機械設計與研究，2005，21(4)：47-50．

[7] 李金蓮．雙圓弧齒輪凸、凹齒同時加載的齒腰彎曲應力[J]．機械設計與研究，2009，25(4)：53-55.

[8] 張志強，唐 勇，賀 靜，等．任意轉角位置的雙圓弧齒輪的齒面數學模型[J]．機床與液壓，2005(6)：26-29.

[9] 唐 勇，許 焰，賀 靜．雙圓弧齒輪精確建模與分析[J]．長沙大學學報，2006，20(2)：47-49．

[10] 李金蓮，夏建芳，張志強．雙圓弧齒輪的彎曲應力分析[J]．機械研究與應用，2009(2)：16-18．

[11] 黃利銀，李金蓮．雙圓弧齒輪齒根曲率半徑對齒根應力的影響[J]．機械設計與研究，2011，27(3)：56-59.

[12] 邵家輝．圓弧齒輪[M]．北京：機械工業出版社，1994.