關節臂式柔性坐標測量機測量空間分析

合肥工業大學 柯 龍

傳統的笛卡爾式正交坐標測量機[1]由于體積大、結構復雜、造價昂貴，而且受相互垂直的導軌和安裝環境的限制，因此有量程小、不易實現在線測量等缺點，不能滿足很多場合的應用要求。隨著柔性化和在線測量等要求的不斷提出，新型非笛卡爾式的柔性關節臂式坐標測量機以其便攜、靈活、造價低、量程大的特點發展迅速，應用也愈發廣泛，測量精度也越來越高，適宜于工業現場的使用。

1.測量機結構

關節臂式柔性坐標測量機的結構設計模仿了工業機器人手臂的構造，如圖1所示，測量機由基座、3根測量臂、6個轉動關節和一個接觸式測頭組成，6個轉動關節處安有圓光柵角度傳感器，前端的測頭通過接觸被測工件觸發信號，此信號被反饋給計算機處理系統，再結合各個旋轉關節處圓光柵讀取的關節轉動角度值，通過程序的運算，得到被測量點處的坐標值（如圖1所示）。

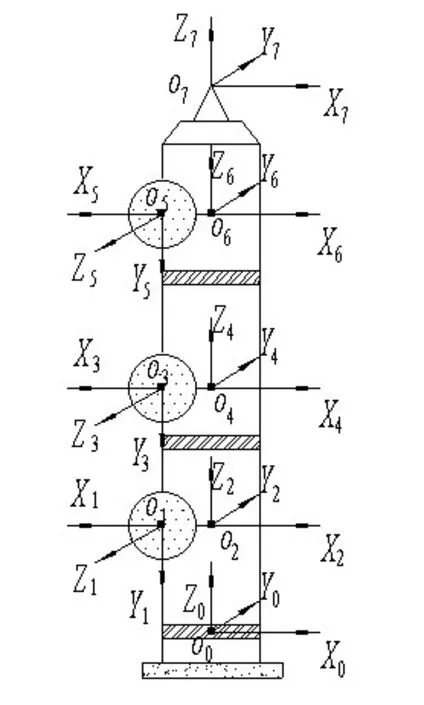
圖1 被測量點處的坐標值

2.測量機數學模型

由關節臂式柔性坐標測量機的結構形式不難看出，其結構類似于工業生產中的機器人手臂，因此關節臂式坐標測量機的模型建立也可以參照工業機器人的建模方法。Denavit和Hartenberg[2，3]在1955年提出了兩個相互連接且相對運動的構件之間相互關系的分析方法，D-H方法是在兩個相互連接且相互運動的桿件上各自固定一個坐標系，然后用一個4×4的齊次變換矩陣即D-H矩陣來描述相鄰兩連桿的空間關系。通過依次變換可最終推導出末端點位置相對于基座坐標系的位置，從而建立坐標測量機系統的數學模型。利用齊次變換矩陣我們可以表示為T07=T01T12T23T34T45T56T67，模型參數包含有桿件的長度li、桿件的扭角iα、關節變量iθ和桿件i的偏置量di（i=1，2，…，6）。其測量模型，如式(1)所示。

3.測量空間分析

柔性關節臂式坐標測量機的測量空間我們可以定義為測量機處于正常工作狀態下，末端測頭所能測量到的空間中所有點位置的集合。在理想狀態下，測量機的測量空間應為一實心球體，并且測頭能夠探測到空間內的任意一點。但是在實際情況當中，由于受到測量機結構的影響，除去基座位置因為固定不動而不能測量到以外，測量機的測量空間有可能會出現測量“死角”，如圖情況下所示的“空腔”位置，也就是測量機測頭無法探測到的區域。當測頭長度l，桿件偏置d3，d5桿長l4滿足時會出現如圖2(a)所示的空腔，該測量空腔球徑為，而當d3≤d5-時，坐標測量機會出現圖2(b)所示的空腔情況，此時的球徑，由上述關系我們可知，要想不出現如圖所示的空腔，必須滿足即

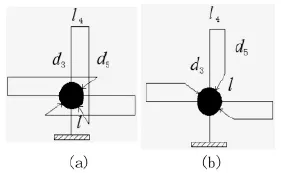
圖2

圖3 抽樣的點的集合

4.測量機測量空間

對于前面關節臂式柔性坐標測量機測量空間中存在測量“死角”的問題，我們可以通過尋找坐標測量機的測量空間來進行驗證。我們借鑒工業機器人工作空間[4]的分析方法。機器人工作空間的分析方法主要有：幾何法、解析法及數值法。針對我們坐標測量機的機械結構及測量模型，我們選擇數值法當中的蒙特卡洛法[5-7](Monte Carlo)，它是一種采用隨機抽樣來解決數學問題的數值方法，廣泛用于物理模型的建立、金融工程學、生物醫學、空氣動力學、宏觀經濟學等。通常利用蒙特卡洛方法處理問題的步驟如下：

(1)描述并確定數學問題的概率模型；

(2)在隨機樣本中進行隨機抽樣；

(3)將樣本代入到模型當中進行統計估計。

我們坐標測量機的測量空間可以表示為如下的形式：

上式中，S表示空間中點的集合，P為末端測頭處點位置坐標，f為坐標測量機測量模型，θi為廣義關節變量，Q為關節變量取值范圍，R3表示三維空間。測量機模型前面已經給出即坐標測量機測量模型，廣義關節變量即我們的隨機抽樣樣本需要通過隨機數的產生來獲得。

首先我們利用RAND函數來產生均勻分布的[0，M]隨機數即我們進行抽樣分析的隨機樣本，我們取M=106，使×RAND÷M，其中θ分別為關節變量的最大、最小值。這里我們取十萬組隨機樣本即十萬個形態位姿，將這些隨機樣本代入式(1)中的模型，我們便可以得到各個測頭點位置處的坐標(xi，yi，zi)。

利用軟件進行模擬仿真，我們可以得到所抽樣的點的集合，如圖3所示，即為關節臂式坐標測量機的測量空間，所取樣本數越多，測量空間就越精確。從圖上我們可以看到該測量空間為一完整的曲面球體，并沒有出現前面所討論的存在測量“死角”的情況，也反映了我們坐標測量機結構參數設計的合理性。

5.結論

本文闡述了關節臂式坐標測量機的結構與數學模型，并基于結構討論了測量機測量空間中測量“死角”的情況，采用了蒙特卡洛理論對測量空間進行了分析與軟件仿真，驗證了我們坐標測量機測量空間當中并無測量“死角”的存在，證明了我們坐標測量機結構設計的合理性。為我們今后找尋坐標測量機的空間誤差分布規律與最佳測量區域奠定了理論基礎并提供了幫助。

表1 柔性坐標測量機的結構參數

[1]張國雄.三坐標測量機[M].天津:天津大學出版社,1999:1-3.

[2]于連棟,程文濤,費業泰.基于激光跟蹤儀的關節式坐標測量機參數標定[J].中國科學技術大學學報,2009,39(12):1329-1332.

[3]汪平平.柔性坐標測量機精度理論及應用技術研究[D].合肥:合肥工業大學,2006.

[4]王興海,周迢.機器人工作空間的數值計算[J].機器人,1988,2(1):50-53.

[5]Rastegar J,FardaneshB.Manipulator workspace analysis using the Monte Carlo method[J].Mechanism & Machine Theory,1990,25(2):233-239.

[6]曹毅,王樹新,李群智.基于隨機概率的機器人工作空間及其解析表達[J].組合機床與自動化加工技術,2005(2):1-6.

[7]張孝澤.蒙特卡羅方法在統計物理中的應用[M].河南:河南科學技術出版社,1991.