在Word界面上實現(xiàn)矩陣操作

呂洪升

（巢湖學院，安徽 巢湖 238000）

數(shù)學教學中，數(shù)據(jù)處理、繪圖等費時費力，且無論用PowerPoint還是Word設(shè)計教案，所插入的數(shù)學公式不能與其它文字統(tǒng)一處理，必須單獨編輯，就這一點，教師備課就得花不少無謂時間，何況數(shù)學公式軟件只能編輯公式而不能實現(xiàn)數(shù)據(jù)分析或計算呢。為化解這個矛盾，本人在概率統(tǒng)計和離散數(shù)學教學中引入工程軟件Matlab作為后臺工具，在PowerPoint或Word界面上無縫隙鏈接Matlab的強大數(shù)據(jù)處理、繪圖和簡單模擬等功能[1]，而不用考慮學生是否具備Matlab程序設(shè)計語言的基礎(chǔ)，也不用刻意補充講授該語言的各種規(guī)定和程序設(shè)計的語法體系，取得了良好的教學效果。作為教學經(jīng)驗總結(jié)或教學研究，這里試圖將Matlab作為矩陣教學的后臺工具，仍在Microsoft-Word平臺上介紹矩陣的各種操作，以提高高等代數(shù)課堂教與學的興趣和教學效果。

1 引例

求一個已知矩陣A（在解題中給出）的行列式、逆矩陣B、特征值D和特征向量V。

1.1 解題過程

解 （只需兩步：輸入、選擇執(zhí)行 ）。

第一步：輸入

第二步：選擇執(zhí)行（圖1）

結(jié)果如下：

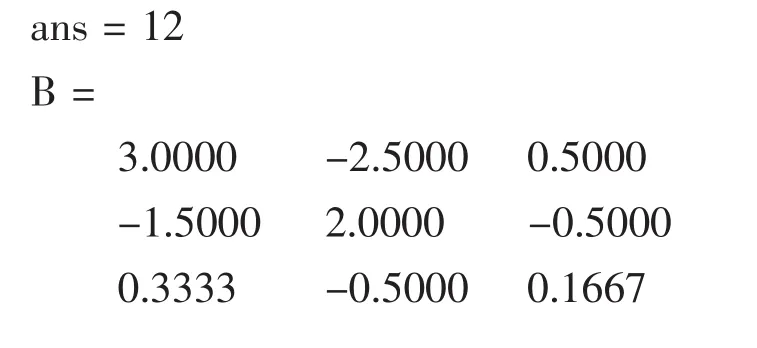
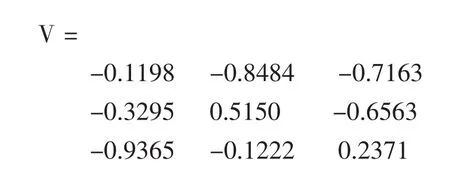
圖1

1.2.1 錄入數(shù)據(jù)和指令：（1）輸入矩陣 A，所有元素必須放在矩陣標識符——中括號 “[]”內(nèi)，逗號“，”或空格”分隔矩陣列，分號“；”或回車鍵“”分隔矩陣的行[1]；（2）輸入求矩陣行列式函數(shù)“det”、求逆矩陣函數(shù)“inv”和特征值、特征向量函數(shù)“eig”[1]。

1.2 解題步驟和顯示規(guī)律分析

1.2.2 執(zhí)行計算： 選中輸入的四行字符，擊“加載項/notebook/Evaluate Cell”菜單（見圖1），選中文字立刻變成綠色，計算結(jié)果以藍色字符顯示。

1.2.3 結(jié)果顯示的一般規(guī)律：執(zhí)行指令后，若有結(jié)果輸出，一般依次顯示在選中行的下方。命令行左邊若有字母和賦值號“＝”，結(jié)果就賦給該命令左邊的字母（如第三行的逆矩陣B），若左邊沒有任何符號，結(jié)果一律用“ans”表示（如第二行的行列式值12）；要不想顯示某個指令的輸出結(jié)果，就在該指令行后面加“;”且與該行一并選中[1]（如第一行的矩陣A）。第四行的“eig”函數(shù)有些特別，它同時求得矩陣特征向量、特征值，并分別用V和D表示。

1.2.4 解題分析：通常情況下，即使矩陣 A不太復雜，課堂上動態(tài)解答這一結(jié)果也是不太容易的，而在引例環(huán)境下，只要熟悉三個指令，輸入四行，選擇一下希望輸出的結(jié)果，計算機就會現(xiàn)場給出答案，而且輸入的公式或輸出的數(shù)字符號等可與其它文字統(tǒng)一編輯，大大方便了數(shù)學教案的個性化編排。再看解題結(jié)果，輸入的四行數(shù)據(jù)都變成了綠色，且被一對灰色中括號括住，這就是Word中能與Matlab接口并可被其執(zhí)行的指令，稱為輸入細胞；第二、三、四行執(zhí)行結(jié)果被以藍色字符顯示，是系統(tǒng)執(zhí)行該輸入細胞的結(jié)果，稱為輸出細胞，第一行A因為后面的“；”而不顯示。

1.2.5 運行平臺剖析：這是一個Word平臺上的矩陣操作實例，是在工程軟件Matlab打開的前提下，利用兼Word文字處理和工程計算功能為一體的notebook核心模板M-book界面，從后臺調(diào)用了Matlab的函數(shù)或命令，前臺卻完全看不到，學生感到只要熟悉幾個功能函數(shù)或命令就能得到想要的計算結(jié)果，這種拿來即用的簡單工具師生都會喜歡，無論直接用于數(shù)學教學還是作為數(shù)學驗證，都是難得的好幫手。不論概率統(tǒng)計、離散數(shù)學還是微積分中繪圖、求導、求積分和解微分方程等，都有對應取之即用的簡單指令，對數(shù)學教師而言，最實用的可能是符號運算。而在信息科學和自動控制領(lǐng)域或教學中，該軟件更有用武之地。

2 數(shù)學教學中如何配置和使用notebook

從上面引例看到，我們的操作界面就是微軟的文字處理軟件Word，對現(xiàn)在任何一個大學生，使用都不會有問題。如何配置，也易如反掌，但我們的目的是在不增加學生學習負擔的前提下使用Matlab的簡單函數(shù)和基本命令，久而久之，學生不僅感覺方便、有趣且離不開，而這種解釋式、能集Fortran、Pascal、C語言等于一體的第四代程序設(shè)計語言[2]很簡單，易于掌握且功能特別強大，有數(shù)學教學中使用的基礎(chǔ)，學生一定會無師自通的。

下面簡述如何配置計算機并進入引例的環(huán)境。

2.1 Matlab的安裝和運行。早期的Matlab，由于容量大，安裝費時費力，很不容易，現(xiàn)在有綠色便攜版或云軟件系統(tǒng) （百度一下就有許多資源），只要下載到U盤中，在任一部裝有Windows XP或Windows 7操作系統(tǒng)的PC機上就能即插即用，不用安裝，非常方便，當然在Unix平臺上使用也簡單，不需贅述。

2.2 notebook安裝。本機使用的操作系統(tǒng)是Windows 7，且假定已安裝了Microsoft Word2007（Windows和Word其它版本操作類似）。首先運行Matlab軟件，在其命令窗口輸入notebooksetup回車 （這里要注意notebook與后面 “-setup”的減號之間要空一格，否則系統(tǒng)報錯，安裝失敗），在歡迎界面中鍵入Microsoft Word2007前面的數(shù)字5（圖略），就完成了安裝。

2.3 notebook啟動，無論在Matlab還是在Word2007環(huán)境下，都有多種啟動方法。

在Matlab命令窗口，鍵入notebook，回車，新M-book模板文檔即可供編輯，操作的窗口就是我們常見的Word2007界面；

若先打開Word，擊“新建/我的模板/M-book.dot”文檔（見圖2），擊“確定”按鍵即進入空文檔編輯狀態(tài)。

圖2

編輯或打開已有文檔與Word通常操作完全一樣。

3 涉及矩陣處理的常用命令

學生沒有Matlab基礎(chǔ)，教師在課堂上直接使用Matlab簡單函數(shù)處理數(shù)學教學中的數(shù)據(jù)問題，為引導學生逐漸熟悉和掌握Matlab部分功能，除課堂使用中自然介紹Matlab常用命令或函數(shù)的基本功能和調(diào)用格式外，還要講述在M-book中輸入的函數(shù)如何被執(zhí)行，執(zhí)行結(jié)果又以什么格式顯示和如何被調(diào)用等，以下逐一說明。

3.1 用于矩陣操作的常用命令

3.1.1 常規(guī)運算符號。Matlab以矩陣為基本操作元素，所以矩陣的加（+）、減（-）、乘（*）、乘方（^）、轉(zhuǎn)置（' ）（當然還有左除、右除和按位乘、除等，有興趣者請查看相關(guān)資料）象小學算術(shù)里四則運算一樣簡單好用，輸入格式就是英文字符環(huán)境下普通Word文本格式。

3.1.2 特殊矩陣生成。普通矩陣的生成方法如引例的第一行A，但一些特殊矩陣有專門的函數(shù)生成，如ones、zeros、eye分別生成單位矩陣、全0 和全 1 矩陣[1]，magic、rand（randn）、diag、compan分別生成魔方矩陣、隨機矩陣、對角矩陣和伴隨矩陣。線性代數(shù)中常用的Pascal、范德蒙矩陣可用函數(shù)Pascal和vander生成[1]，想了解更多或每個函數(shù)的詳細用法，可借助“help”命令尋求幫助，輸入 “help vander”后回車，屏幕即顯示范德蒙函數(shù)的使用信息（如下文的幫助文字），想知道m(xù)agic 的詳情，只要將“help vander”后面的“vander”用“magic”替代即可，如法炮制，可查詢?nèi)魏魏瘮?shù)的使用詳情。

綠色文字“help vander”是輸入細胞——用戶請求信息，其后藍色的輸出細胞——計算機反饋給用戶的幫助文字只保留了一部分，不僅顯示范德蒙函數(shù)的用法，還給出了范德蒙矩陣的定義。

例題1 創(chuàng)建3階均勻分布、正態(tài)分布隨機矩陣和5階范德蒙矩陣。

解 輸入對應的三個生成函數(shù) （每個函數(shù)一行），其它操作同引例，結(jié)果如下：

從輸出結(jié)果可知矩陣生成函數(shù)的用法（其它函數(shù)類似），矩陣A是一個[0，1]上均勻分布的3階隨機矩陣，因為行末尾有“；”未顯示，B是3階標準正態(tài)分布隨機矩陣，C是所需的5階范德蒙矩陣，這里要注意第 3 行函數(shù) vander（1：5）括號內(nèi)的不同形式。

至此，引例中矩陣A、B已被重新賦值。一般情況下，只要本機不重新啟動且A、B沒有被重新賦值，A、B的數(shù)據(jù)保持不變，且隨時隨處可調(diào)用。

例題2 求矩陣A與B的積M。

解 輸入計算公式M=A*B，再設(shè)其為有結(jié)果輸出的輸入細胞（同引例）。結(jié)果如下：

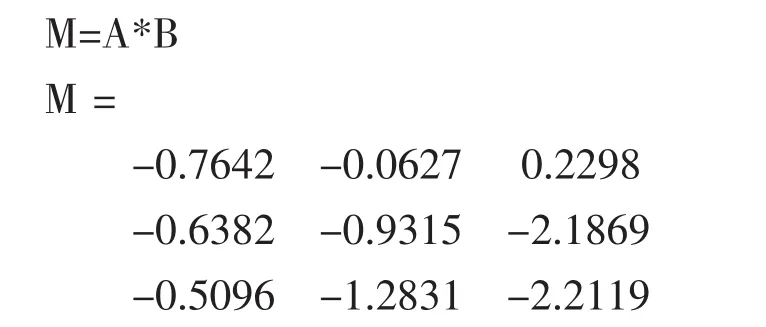
顯然計算結(jié)果是例題1中兩個3階隨機矩陣的積。

若微機重啟后（或下次課）仍需使用以前數(shù)據(jù)矩陣A、B時，只要將原始錄入數(shù)據(jù)對應的行（最好行后加“；”）選中后，設(shè)為有結(jié)果輸出的輸入細胞（擊“/notebook/Evaluate Cell”菜單，見圖1）即可，不需重新輸入矩陣A、B。但要注意，若將例題1中三行如是執(zhí)行后，矩陣A、B已不一樣，因為隨機函數(shù)每次生成的矩陣都不相同[3]，除非設(shè)置重現(xiàn)，矩陣C保持不變。

如果希望一個矩陣每次課都能直接調(diào)用，就在輸入時定義其為自初始化細胞且永不被重新賦值。

3.1.3 常用的矩陣函數(shù)。除引例中介紹的求方陣的行列式、逆矩陣、特征值和特征向量函數(shù)外，rank可求矩陣的秩；其實引例中eig（A）是可對角化方陣A的特征分解函數(shù)，當A不可對角化（特征向量線性相關(guān)）時可用Schur（A）對A作科利分解，稍微推廣，還有針對正定矩陣的Cholesky分解和一般矩陣的LU分解、QR分解、SVD分解[4]，分解名即函數(shù)名，使用與特征分解一樣，都非常方便。另外，兩個矩陣拼接函數(shù)也很實用，horzcat（A，B）是將兩個同行矩陣A、B水平合并成一個大矩陣，而函數(shù) vertcat（A，B）能將兩個同列矩陣A、B垂直合并成一個矩陣。例如，判斷線性方程組AX=B是否有解，只要用語句K=horzcat（A，B）合并A、B得到增廣矩陣K，再計算矩陣A、K的秩 rank（A）、rank（K）就知道方程是否相容了。

3.1.4 矩陣信息和矩陣元素尋訪。矩陣最基本的信息是其尺寸，即矩陣維數(shù) （包括高維矩陣）、各維的長度和元素個數(shù)，分別用函數(shù)nidims、numel和size獲取。矩陣元素尋訪有常用的雙下標方式和單下標方式，雙下標命令A（i，j）很自然讀取矩陣A的第i行第j列元素，如果輸入C（3，2），再選擇執(zhí)行（圖1），立刻得到結(jié)果：

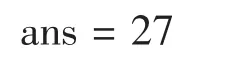
但單下標讀取與其它語言不同，Matlab規(guī)定先列后行[3]，如果我們用C（：）將矩陣C轉(zhuǎn)換成一個列向量（第二列接在第一列后面，第三列接在第二列后面……，依次類推），就知道矩陣C雙下標元素 C（3，2）對應單下標元素 C（8）了。一般地，若A是一個m×n矩陣，則A的雙下標元素A（i，j）對應其單下標元素是 A[m×（j-1）+i]，反過來也容易推算。另外，函數(shù)max（或min）可以找出矩陣每一列的最大值（最小值），很自然，max（max（A）（或 min（min（A））能求出整個矩陣的最大值（或最小值），而[MaxValue,MaxIndex]=max（A（：））還能輕松獲得A的最大值和最大值單下標索引號。

例題3 求矩陣的最大元素及其對應位置。

解 輸入矩陣D和相應函數(shù)

選中并擊“notebook/Evaluate Cell”菜單執(zhí)行

得到所需的輸出結(jié)果

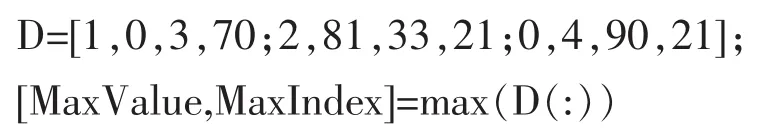
——上兩行是輸入細胞（信息），以下兩行是輸出細胞（微機反饋的計算結(jié)果）

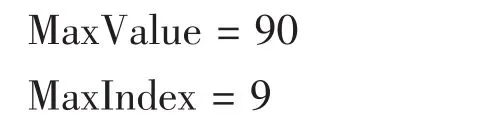
這個結(jié)果表明D（9）=90是矩陣D的元素最大值。

3.2 輸入細胞和輸出細胞

在Word平臺上使用Matlab的矩陣操作指令，自然有一個信息交換過程。其實我們將Matlab當成了隱蔽的加工廠，在前臺，將制造所需產(chǎn)品的原料或零配件（如引例中輸入的矩陣和所使用的Matlab矩陣操作函數(shù)）打包待用（選中），擊“加載項/notebook/Define input Cell”菜單（見圖1）或按快捷鍵“Alt+D”，選中的指令立即變成“綠色”且被一對灰色中括號括住，表示選中部分已被設(shè)成了“輸入細胞”，但沒有加工，所以無輸出結(jié)果，若要將“輸入細胞”加工成產(chǎn)品——輸出細胞，就擊“notebook/Evaluate Cell”菜單或按快捷鍵“Ctrl+Enter”，輸出細胞將以“藍色”字符顯示。暫時放在加工廠的中間產(chǎn)品其對應輸入細胞后面就用英文字符下分號“;”標明。每次一開工就要運往加工廠加工的零配件，可以選中后擊“加載項/Notebook/Define AutoInit Cell”菜單，將其設(shè)成自初始化細胞。

3.3 注意事項

首先，文中列出了Word平臺上矩陣操作的常用函數(shù)，從矩陣教學的角度講，這些功能足以將教師從矩陣計算中解脫出來，教師能將更多精力用于矩陣概念和方法的講授上。其次，文中的所有Matlab指令、標點符號等必須在英文字符狀態(tài)下輸入，以免出錯或死機。第三，盡管notebook已很好地兼容了Word和Matlab的功能，但Matlab的完整程序語言、交互式操作、動畫和Simulink仿真都不能被調(diào)用，這就提醒讀者推廣使用時注意或者直接使用Matlab。

4 推廣使用

本文盡可能簡單地介紹了關(guān)于矩陣處理的幾個基本指令，而涉及高等數(shù)學的所有計算、作圖、統(tǒng)計分析等都有對應的Matlab函數(shù)，且只要知道其名稱就能象文中一樣自如應用，期待更多人通過這里簡單的使用能重視和推廣工程軟件Matlab在各科教學中工具作用，保持傳統(tǒng)教學觀念的同時兼顧一下新技術(shù)手段進課堂的教學嘗試，為所教的學生將進入信息社會做些鋪墊。我們應該承認，各種方法或功能，只要學生知道其存在、實用，學生一定會學習和掌握它，并且探究的信心、推廣的能力可能會大大超出教師的預想。

[1]董霖.MATLAB 使用詳解[M].北京：電子工業(yè)出版社，2009：483，32，113-120，1，26，33，42，19.

[2]劉維.精通Matlab與C/C++混合程序設(shè)計[M].北京：北京航空航天大學出版社，2012.

[3]薜志涌.精通 Matlab[M].北京：北京航空航天大學出版社，2012：1，40，55.

[4]史榮昌.矩陣分析[M].北京：北京理工大學出版社，1998：142-145.