含瓦斯煤固氣耦合動力學模型及其應用研究

劉 軍 ，孫東玲，孫海濤，林府進

(1.中煤科工集團重慶研究院瓦斯分院，重慶 400037；2.瓦斯災害監控與應急技術國家重點實驗室，重慶 400037)

煤的滲透性是煤層氣開發過程中關鍵因素，孔隙壓力、有效應力以及基質收縮/膨脹對煤的滲透性具有重要影響[1]。 “動態滲透率”這一關鍵性因數，已得地面煤層氣開發的廣泛認可[1-2]。煤層氣開發中廣泛應用的P-M、Seidle-Huitt模型和Shi-Durucan模型，其共同點是假設煤巖體處于單軸應變狀態以及豎向應力恒定的基礎上,該假設的合理性有待商榷，特別研究采動影響下煤層開發，以上模型還有待改進[4-7]。周軍平、汪志明等[8-9]建立了包括孔隙壓力、有效應力以及基質收縮耦合作用動力學模型,但是并沒有考慮到瓦斯流動中吸附擴散作用。隨著研究的深入，建立綜合考慮考慮孔隙壓力、有效應力以及基質收縮耦合作用的固氣耦合模型對煤層氣勘探、開發和開采工藝確定、產能預測及預防瓦斯突出等將起到重要作用[10]。因此，本文在廣大學者研究的基礎上,綜合考慮各因素，建立含瓦斯煤固氣耦合動力學模型，并將其應用到生產實踐。

1 含瓦斯煤固氣耦合動力學數學模型

1.1 動力學模型的基本假設

模型引入如下假設：①含瓦斯煤是一種均質彈性體；②煤層被單相瓦斯飽和且溫度恒定；③煤層瓦斯在孔隙-裂隙多重介質中滲流符合Darcy定律，擴散符合Fick擴散定律，并不考慮煤層基質塊與裂隙質量交換；④吸附/解吸以及煤巖裂隙瓦斯壓力變化會使煤顆粒體積應變發生改變，且產生應變在三個方向上相等。

1.2 動力學模型應力場方程

應力場變化服從應力方程、平衡方程、本構方程。

1)應力方程

由太沙基有效應力原理，有效應力方程為

由式(1)、式(2)得到總應力方程

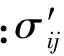
2)平衡方程

3)本構方程

根據假設，煤體在彈性變形階段遵守廣義的胡克定律，即

式中，λ為拉梅常數；εv為體積應變；G為剪切模量；δij為Kronecker符號。

多孔介質煤體的變形包含本體變形和結構變形[11]。結構變形主要是外應力引發煤粒之間位置相對錯動產生的整體變形，是永久性塑性變形。本體變形主要包括熱膨脹變形、吸附瓦斯膨脹變形和煤體骨架受瓦斯壓力的壓縮變形。在忽略溫度變化前提下，煤體的本體變形只有：吸附瓦斯膨脹變形和煤體骨架受瓦斯壓力的壓縮變形。即認為含瓦斯煤層受到地應力和作用在煤體單元孔裂隙結構中的瓦斯壓力以及瓦斯吸附膨脹產生的膨脹應力而發生變形。吳世躍[12]針對吸附瓦斯膨脹變形進行深入研究，從理論上推導了煤體膨脹應力和膨脹應變的計算公式。

式中：σsw為吸附膨脹應力，Pa;εsw為吸附膨脹應變，％；a為極限吸附量，m3/kg；b為吸附常數，MPa-1；R為瓦斯摩爾常數，8.3143J/(kg·K)；T為煤體溫度，K；υ為泊松比；Vm為摩爾體積，22.4×10-3m3/mol；P為孔隙壓力，MPa；ρc為含瓦斯煤體視密度，kg/m3。

在工程實踐中[13-16]得出，因孔隙流體壓力變化而引起的固體顆粒體積變化而引起的變形由式(8)表示。

式中：εp為瓦斯壓力引起的應變；Δp為瓦斯壓變化，MPa。

將于煤體的本體變形表示為：εs=εsw-εp，所以有式(9)成立。

根據式(2)、式(9)求的σij的表達式

σij=

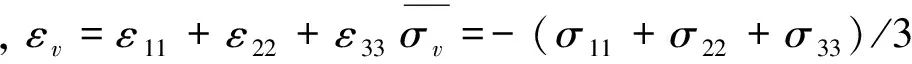
1.3 瓦斯流動方程

煤體是孔隙-裂隙的雙重介質體，包含孔隙系統和裂隙系統，假定瓦斯在裂隙系統中以滲流形式運動，在孔隙系統擴散運動。而瓦斯流動數學模型包含了瓦斯流動連續性方程、瓦斯運動控制方程、煤層瓦斯狀態方程和瓦斯含量方程四個基本方程組成，以下是分別對以上四種方程的描述。

1.3.1 連續性方程

瓦斯的在裂隙系統和孔隙系統中連續方程為式(13)、式(14)，在孔隙-裂隙二重介質中，裂隙中自由煤層氣的滲流量比孔隙系統中吸附煤層氣擴散要大得多，所以可以忽略孔隙系統通過擴散直接進入鉆孔或煤壁的氣體，而僅把孔隙系統的擴散解吸看作向裂隙系統補給的內質量源，此時煤層氣的擴散滲流方程組就由煤粒吸附煤層氣擴散方程與裂隙系統滲流方程，所以得到瓦斯流動連續質量方程(15)。

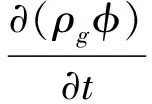
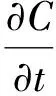
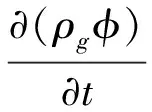
式中：C為單位體積煤層所含有吸附狀態煤層氣的質量濃度，kg/m3；ρg為瓦斯壓力p時瓦斯氣體密度，kg/m3；Jc為擴散流體通過單位面積的擴散速度,kg/(s·m2)。

1.3.2 流動的方程

1)煤層瓦斯滲流的狀態方程。鉆孔抽采下煤層瓦斯在煤體內的流動符合Darcy滲流規律[17]。

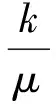
當氣體在煤巖多孔介質中流動時,由于氣體分子平均自由通道程與孔裂隙的直徑處在同一量級上,氣體分子就會與通道壁面相互作用,從而造成氣體分子沿孔隙表面滑移,增加了分子流速,這一現象稱為分子滑移現象[18]。這種由氣體分子和固體分子間的相互作用產生的效應稱Klinkenberg 效應(式(17))，因此考慮Klinkenberg效應的瓦斯滲流運動方程為(18)。

式中：V煤層瓦斯滲流速度矢量，m/s；k為滲透率，k0為初始滲透率，m2；m為klinkenberg系數。

2)擴散運動方程。氣體在多孔介質中擴散滿足Fick擴散定律[19]，寫為

J=-D

式中：J擴散流體通過單位面積的擴散速度,kg/(s·m2)；D擴散系數,m2/s；C擴散流體質量濃度,kg/m3。

1.3.3 狀態方程

根據假設瓦斯被看作理想氣體，瓦斯流動視為等溫過程，則其狀態方程

式中：β煤層瓦斯的壓縮因子，kg/(m3·Pa)，且有：β=Mg/ZRT；Mg為瓦斯氣體分子量，kg/(K·mol)；R為一般氣體常數，kJ/(kmol·K)；T為氣體的溫度，K；Z為壓縮系數。

1.3.4 含量方程[19]

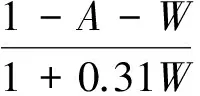
式中：Cf、Ca分別為游離和吸附瓦斯含量，kg/m3；pn為大氣壓；ρn為參考大氣壓下瓦斯密度，kg/m3；φ為煤體孔隙度；A為煤中灰分；W為煤中水分；a為極限吸附量，kg/m3；b為煤的Langmuir壓力參數，MPa-1;ρc為當前壓力下瓦斯密度,kg/m3。

根據式(15)～(21)得出瓦斯流動控制方程

φ+

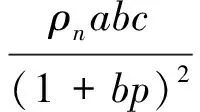
式(22)與式(12)構成了煤層氣與煤層耦合動力力學模型，但二者之間需靠滲透率k和孔隙度φ建立耦合關系。

1.4 動態滲透性與孔隙度模型

Zhang等人[20-23]建立普遍應用的動態孔隙度與滲透率模型，近年來得到廣泛的應用，鑒于文章篇幅不再推導。

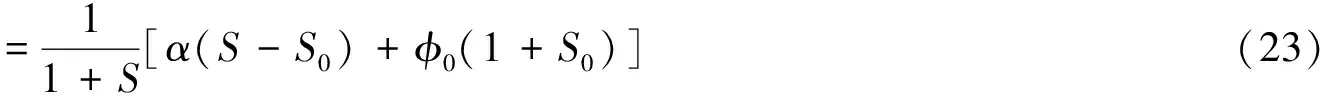
其中

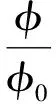
煤是典型的孔隙介質，若煤的體積模量K遠小于煤基質的體積模量Ks,游離瓦斯和吸附產生的變形忽略不計，則上式可以得

式(26)與文獻[13]得到的孔隙度關系式是完全相同的。

式中：εv為當前體積應變；εv0為初始體積應變；εs為現在因瓦斯壓力變化產生變形和吸附變形之和。

式(23)求導得出孔隙率的變化率。

將式(12)、式(22)、式(23)、式(24)、式(27)整理就得到含瓦斯煤層與煤層氣耦合動力學模型，即式(28)。

2 固氣耦合動力學模型應用

固氣耦合動力學模型具有廣泛應用，在此利用該模型借助COMSOL Multiphysics軟件對山西某礦3#煤層順層鉆孔抽采煤層瓦斯有效半徑進行數值求解，驗證模型的同時，也為現場工程起到指導作用。

2.1 幾何物理模型

根據已有研究[24-26]，鉆孔抽放數值分析采用二維平面模型。考慮到工作面的煤層賦存條件、地應力狀態和瓦斯鉆孔抽排設計條件，建立了其幾何物理模型見圖1。物性參數見表1。

2.2 模型的初始條件和邊界條件

在所取研究域內，其初始條件和邊界條件如下。

1)煤層瓦斯初始條件：t=0；p=P0。

式中：P0為煤層瓦斯壓力初始值P0=0.69MPa。

2)分析域內邊界條件為

3)應力場初始位移μ=0；ν=0。

4)應力邊界條件為：煤層頂部邊界上承受著上覆巖層的重量應力為F=6.5MPa ，同時考慮煤體自重，位移邊界條件在分析域的下端邊界y=0以及左端和右端邊界上x=0和x=100為位移約束邊界；r為抽采半徑,p1為抽采負壓。

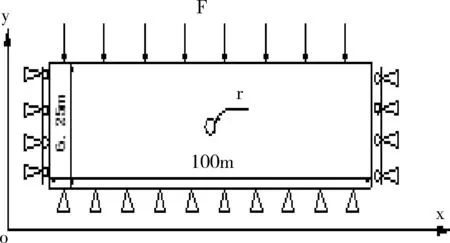
圖1 單一順層鉆孔抽排瓦斯數值模擬的幾何模型

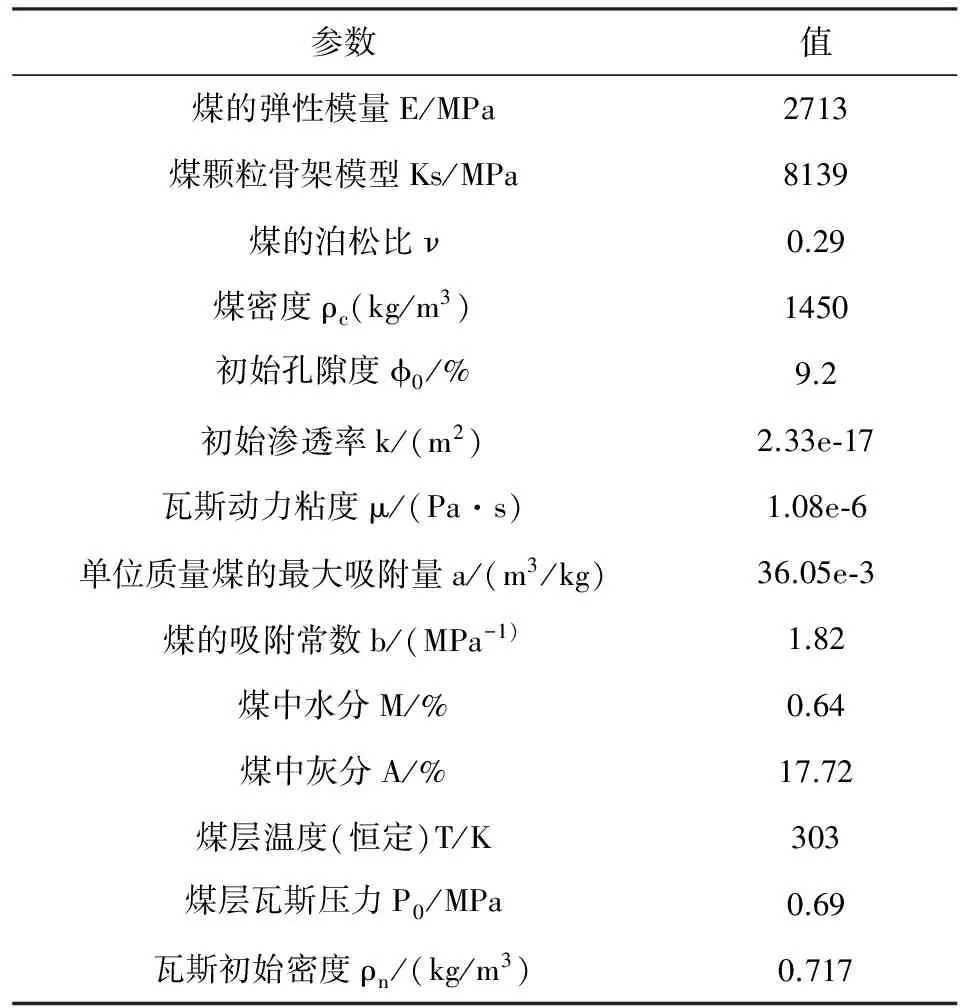
表1 某礦含瓦斯煤層物性參數

3 數值模擬的結果分析

鑒于該礦瓦斯壓力低，用含量變化判定瓦斯抽采效果更佳，因此對瓦斯含量變化進行分析。圖2為不同抽采時間含量的變化圖，圖2中可以看出，隨著抽采時間的增加，瓦斯含量不斷的減小，鉆孔抽采的影響范圍不斷的增加，瓦斯流場范圍在抽采負壓作用下逐漸擴大，為進一步定量描述鉆孔抽采下瓦斯含量的變化，取模型中以點(50，3.125)和點(100,3.125)組成的剖面線，和取點A(51，3.125)、B(52,3.125)、C(55,3.125)以及點D(50,4.125)和E(50,5.125)對上述瓦斯含量變化進行分析。圖3為不同抽采時間剖面線上瓦斯含量的變化圖，圖4為點A、B、C、D、E處瓦斯含量隨時間的變化。

根據圖3、圖4知，鉆孔周圍瓦斯含量下降較快，瓦斯含量梯度較大，但是隨著時間的增加，瓦斯含量減小，瓦斯含量的降低梯度也減小，這說明鉆孔在抽采的初始階段，瓦斯的抽放量很大，經過一段時間之后，瓦斯抽采量將趨于穩定，以上分布圖與文獻[26-28]模擬結果一致。根據圖4中B、E點和A、D點瓦斯含量對比分析知，在同一時間下，距離鉆孔相同距離點的瓦斯含量比水平方向含量降低快，這是因為受到鉆孔開挖致滲透率增加。

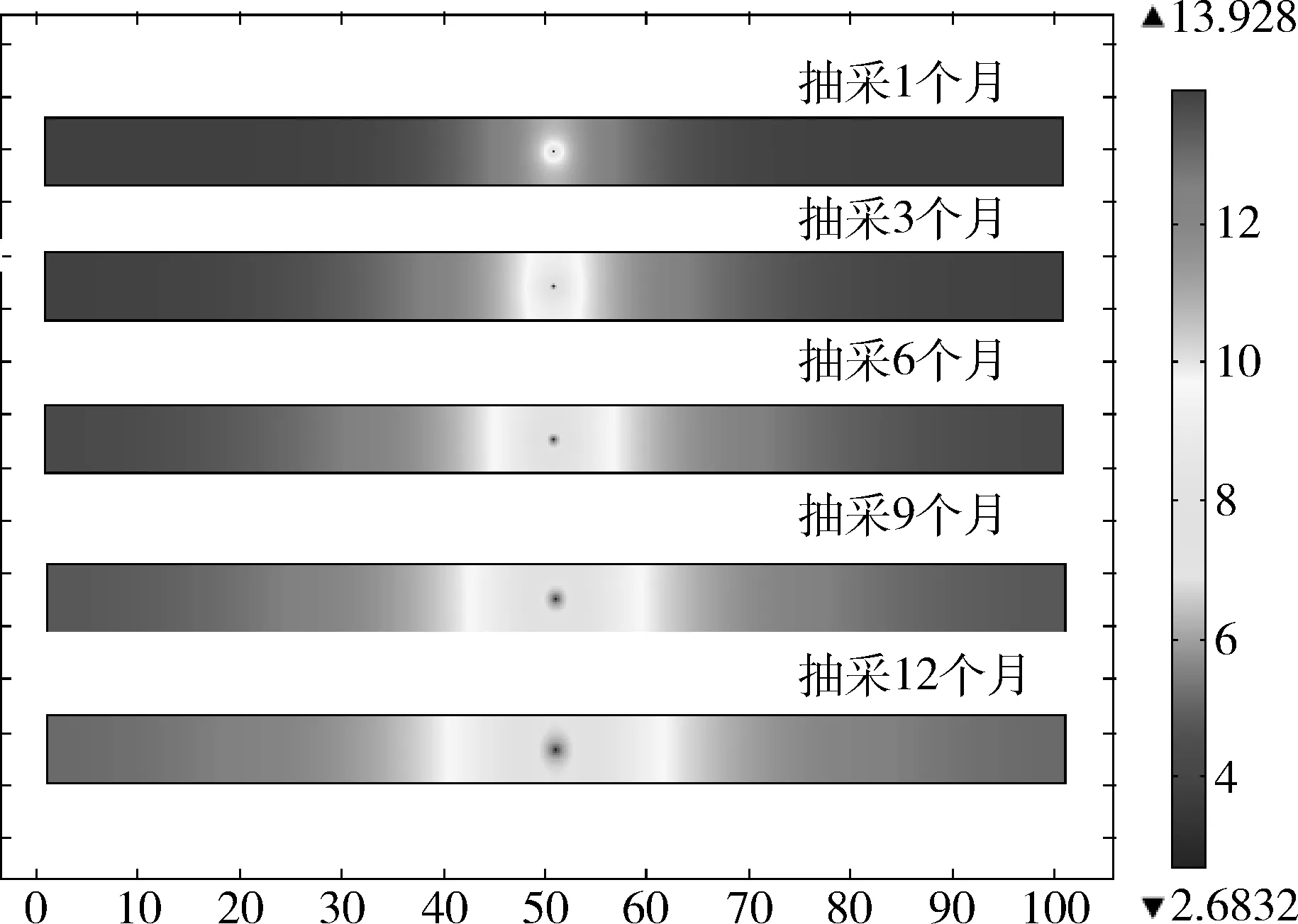
圖2 不同抽采時間瓦斯含量的變化圖

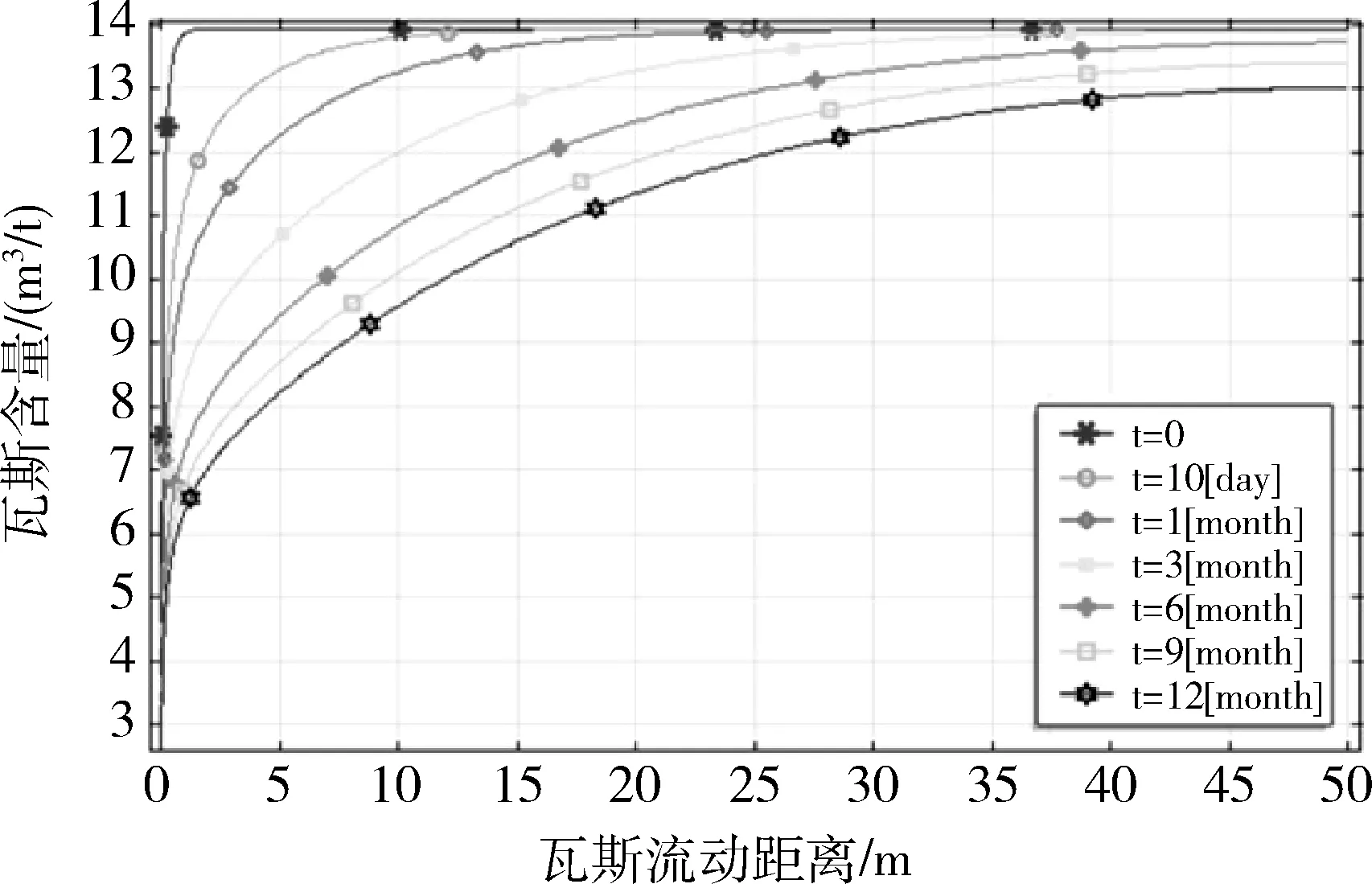
圖3 不同抽采時間剖面線上瓦斯含量的變化圖

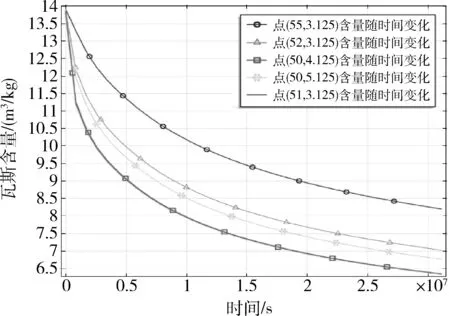
圖4 點瓦斯含量隨時間的變化圖

根據《煤礦瓦斯抽采基本指標》(AQ 1026-2006)中規定，在鉆孔有效抽采半徑內，需將煤層瓦斯含量降到8m3/t。因此，把瓦斯含量降到8m3/t為指標確定鉆孔有效抽采半徑。依靠這個指標根據圖3該礦抽采一年的有效半徑約為4.5m。這一數據與該礦在抽采工程中取得數據以及順層鉆孔合理布置參數實驗得到的半徑基本一致，證明了此數學模型的正確性。最終將鉆孔的間距由原來的5m，提高到7～10m，在滲透率相對低區域鉆孔間距小，滲透率高區域鉆孔間距大。通過對抽采參數監測，最終保證綜放面安全生產預抽率(25％～30％)，取得了良好的抽采效果。

4 結論

從瓦斯流動理論出發，以體積應變為橋梁通過煤層的孔隙度、滲透率方程將煤層應力場方程與瓦斯流動場方程耦合，建立含瓦斯煤固氣耦合動態數學模型。借助多物理場數值模擬軟件，分析本層單一順層鉆孔的瓦斯含量變化，得出特定條件下瓦斯抽采有效半徑,并通過與現場實驗與實際抽采數據分析驗證瓦斯抽采有效半徑正確性。固氣耦合動力學模型的建立將對煤層氣開發和防治煤與瓦斯突出具有理論和工程指導意義。

[1]李培超,孔祥言,曾清紅，等.煤層滲透率影響因素綜述與分析[J].天然氣工業,2002,22(5):45-49.

[2]鄧澤,康永尚,劉洪林，等.開發過程中煤儲層滲透率動態變化特征[J].煤炭學報,2009,34(7):947-951.

[3]郭衍茹,練章華，魏臣興.氣井的流固耦合滲流場分析[J].斷塊油氣田,2012,19(4):481-484.

[4]Seidle J P,Jean sonne M W,Erickson D J.Application of matchstick geometry to stress dependent permeability in coals[ C].SPE 1992,243-261.

[5]PalmerI,MansooriJ.How pemeability depends on stress and pore pressure in coal beds :a new model[J].Soc.Pet.Eng.Res.Eng,1998,12 :539- 544.

[6]趙陽升,胡耀青,楊棟，等.三維應力下吸附作用對煤巖體氣體滲流規律影響的實驗研究[J].巖石力學與工程學報,1999,18(6):651-653.

[7]孫培德.變形過程中煤樣滲透率變化規律的實驗研究[J].巖石力學與工程學報,2001,20(S1):1801-1804.

[8]周軍平,鮮學福,姜永東，等.考慮有效應力和煤基質收縮效應的滲透率模型[J].西南石油大學學報,2009,31(1):4-8.

[9]張健,汪志明.煤層應力對裂隙滲透率的影響[J].中國石油大學學報,2008,32(6):92-95.

[10]狄軍偵,殷志祥,劉建軍.應力作用下煤層氣非穩定耦合滲流模型及數值模擬[J].中國煤田地質,2007,19(4):36-38.

[11]李傳亮,孔祥言,徐獻芝，等.多孔介質的雙重有效應力[J].自然雜志,1999,21(5):288-297.

[12]吳世躍,趙文,郭勇義.煤巖體吸附膨脹變形與吸附熱力學的參數關系[J].東北大學學報：自然科學版,2005,26(7):683-686.

[13]李培超,孔祥言,盧德唐.飽和多孔介質流固耦合滲流的數學模型[J].水動力學研究與進展,2003,18(4):419-426.

[14]付玉,郭肖,賈英，等.煤基質收縮對裂隙滲透率影響的新數學模型[J].天然氣工業,2005,25(2):1-3.

[15]冉啟全,李士倫.流固耦合油藏數值模擬中物性參數動態模型研究[J].石油勘探與開發,1997,24(3):61-65.

[16]陶云奇,許江,程明俊.含瓦斯煤滲透率理論分析與試驗研究[J].巖石力學與工程學報,2009,28(2):3363-3370.

[17]周世寧,林柏泉.煤層瓦斯賦存與流動理論[M].北京:煤炭工業出版社,1990.

[18]Jones F O,Owens W W.A laboratory study of low gas sands[J].J Pet Tech,1980:1631-1670.

[19]楊其鑾,王佑安.煤屑瓦斯擴散理論及其應用[J].煤炭學報,1986(3):87-93.

[20]孫培德.SUN模型及其應用[M].杭州:浙江大學出版社,2002.

[21]Detournay E,Cheng AHD.Fundamentals of poroelasticity[M].In:Fairhurst C,editor.Comprehensive rock engineering,1993,2:113-71.

[22]J.G.Wang a,Akim Kabirb,Jishan Liu.Effects of non-Darcy ?ow on the performance of coal seam gas wells[J].International Journal of Coal Geology,2012(93):62-74.

[23]Hongbin Zhang Jishan Liu,D.Elsworth.How sorption-induced matrix deformation affects gas ?ow in coal seams:A new FE model[J].International Journal of Rock Mechanics & Mining Sciences,2008(45):1226-1236.

[24]Shi J Q,Durucan S.Changes in Permeability of Coalbeds During Primary Recovery Part 1:Model Formulation and Analysis[C].Paper 0341 proc.2003 International Coalbed Methane Symposium,University of Alabama,Tuscaloosa,Alabama(May).

[25]王宏圖,江記記,王再清，等.本煤層單一順層瓦斯抽采鉆孔的滲流場數值模擬[J].重慶大學學報,2011,34(3):24-29.

[26]司鵠,郭濤,李曉紅.鉆孔抽放瓦斯流固耦合分析及數值模擬[J].重慶大學學報,2011,34(11):105-110.

[27]劉清泉,程遠平,王海鋒，等.順層鉆孔有效瓦斯抽采半徑數值解算方法研究[J].煤礦開采,2012,17(2):4-8.