基于UKF、EKF飛行器氣動參數辨識方法比較研究

?

基于UKF、EKF飛行器氣動參數辨識方法比較研究

李正楠，汪沛

（空軍航空大學軍事仿真研究所，吉林長春130022）

摘要：在航空航天工業中，氣動參數辨識廣泛應用于飛機氣動性能測試，隨著飛機性能、操縱要求的提高，以及在線辨識實時性的需要，對氣動參數辨識的精度、速度有了越來越高的要求。該文對擴展卡爾曼濾波模型（EKF）、無損卡爾曼濾波模型（UKF）、飛行器氣動參數辨識模型進行理論分析。而后依據固定翼飛機飛行數據，結合二維飛行器運動模型，分別應用EKF算法、UFK算法對氣動參數進行辨識，對兩者的辨識過程和結果進行比較，為飛行器氣動參數辨識中濾波算法的選擇提供借鑒。

關鍵詞：氣動參數辨識；擴展卡爾曼濾波；無損卡爾曼濾波；飛行器運動模型

收到修改稿日期：2013-06-15

0　引言

空航天工業中，飛行器氣動參數辨識是必不可少的算法應用。其中應用時間最長、最廣泛的非線性濾波技術是擴展卡爾曼濾波（EKF），一直以來普遍應用在各種飛行器氣動參數辨識中。無損卡爾曼濾波（UKF），應用時間較少，相對來說，不如EKF成熟，但作為基于卡爾曼濾波辨識方法的較新理論，在一些方面克服了原有的理論缺陷[1-2]。在本文中，通過真實的固定翼飛機飛行數據，對EKF算法、UFK算法的氣動參數估計性能進行比較，分析飛行器氣動參數辨識中兩種算法的可行性及可能存在的優勢。

1　參數估計模型及濾波模型

1.1遞歸參數估計模型

通過濾波的方法可以把改變參數估計問題轉化為狀態估計問題，依據飛行器系統實際情況，采用連續估計模型，并通過離散時間測量和離散濾波算法達到實時效果。將連續估計模型預測與離散濾波算法相結合[3]。采用連續離散濾波的系統模型的連續狀態空間和離散測量方程如式（1）所示：

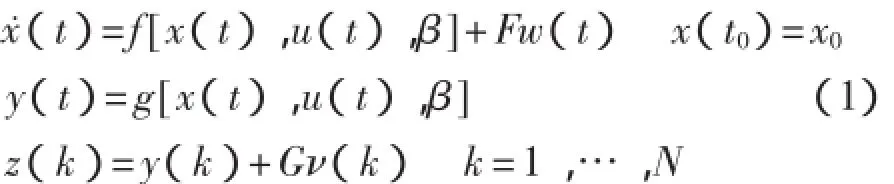
待辨識系統參數向量θ由系統參數β、測量偏差Δz、輸入偏差Δu組成。假設θ為常值。即：

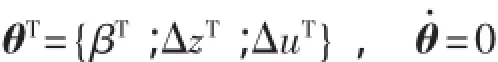
定義增廣向量為

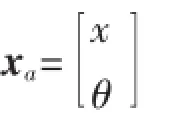
擴展系統化如式（2）所示：

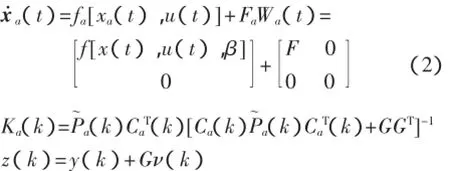
1.2擴展卡爾曼濾波（EKF）模型

EKF通過對非線性函數的泰勒展開式進行一階線性化截斷，從而將非線性問題轉化為線性。

增廣系統狀態向量的均值和協方差如式（3）所示[4]。

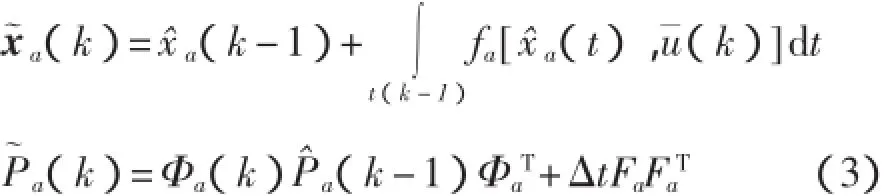
初始值為x贊a（1）=xa0；P贊a（1）=Pa0

其中u軈為第k-1點和第k點的均值或輸入插值，Φa=eAaΔt表示增廣系統的離散時間狀態轉移矩陣。通過式（4）對狀態矩陣進行線性化處理即利用中央差分公式，可在每個離散時間的最佳狀態估計附近通過數值實現線性化。

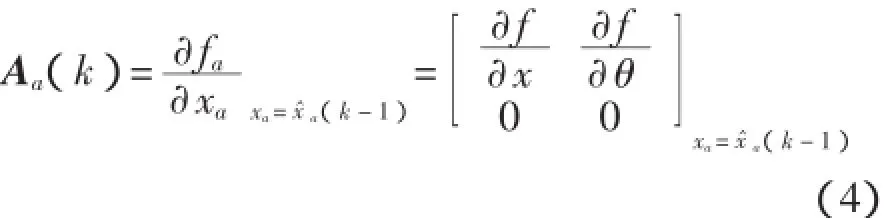
系統更新：

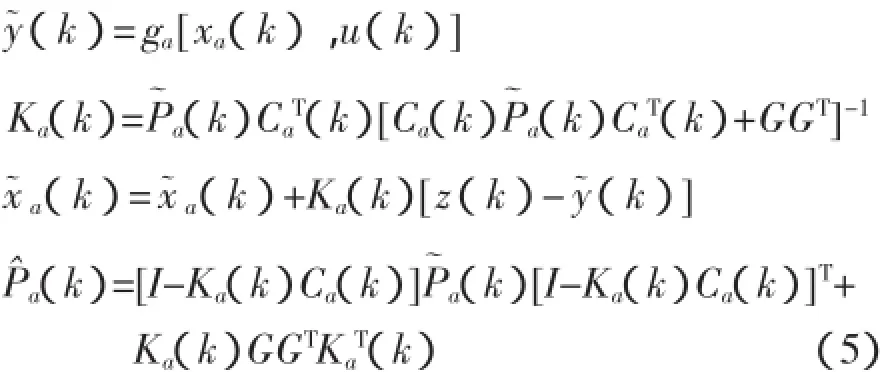
Ca（k）為線性化測量矩陣，在線性化前通過中心差分公式計算：

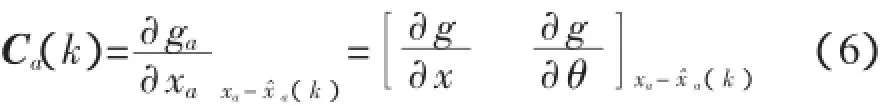
通過龍格庫塔法積分計算式（3），其中狀態轉移矩陣Φa應用泰勒級數展開近似。

1.3無損卡爾曼濾波（UKF）模型

UKF算法的定義2na+1個σ點，（na狀態向量個數）。每個σ點存在一個向量，向量是增廣的狀態向量的預期值，另外2na個點從矩陣平方根列向量±（γP）獲值[5-6]。P是增廣狀態向量xa的協方差矩陣，γ=α2（na+κ）-na。σ點的均值和協方差按式（7）加權：其中權重W計算如下：

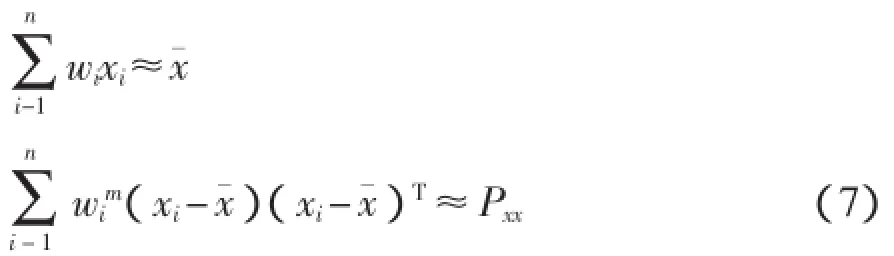
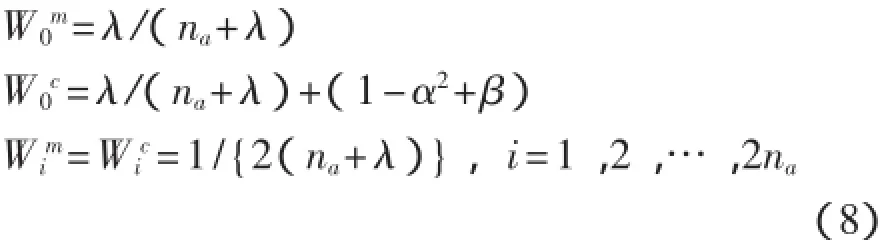
下面以典型的UKF離散應用為例。離散非線性狀態空間模型[7]如下：

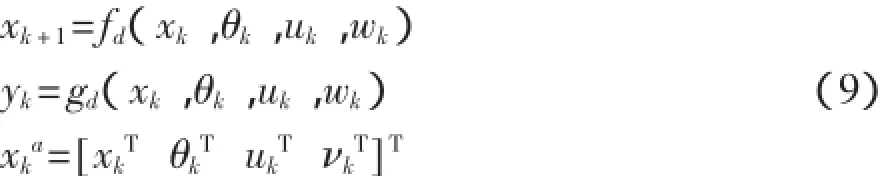
增廣狀態向量和協方差初值為

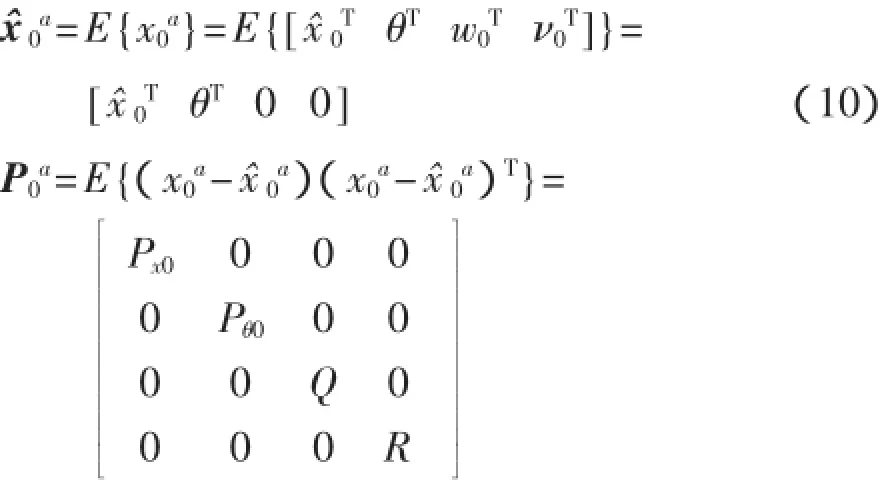
在時間點tk預測概率密度，通過預測和tk時刻測量值計算后驗概率密度。標準的UKF算法總結如下：

（1）設置離散時間點k=1，構建增廣狀態向量x贊ka和相應的協方差矩陣P贊ka，根據式（10）計算初始值。

（2）計算2na+1個σ點

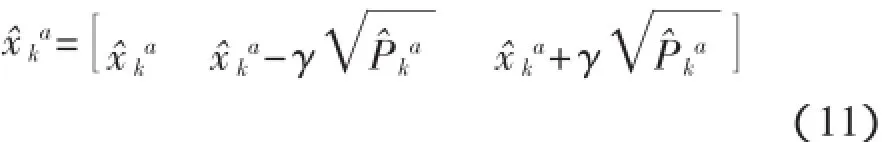
（3）預測

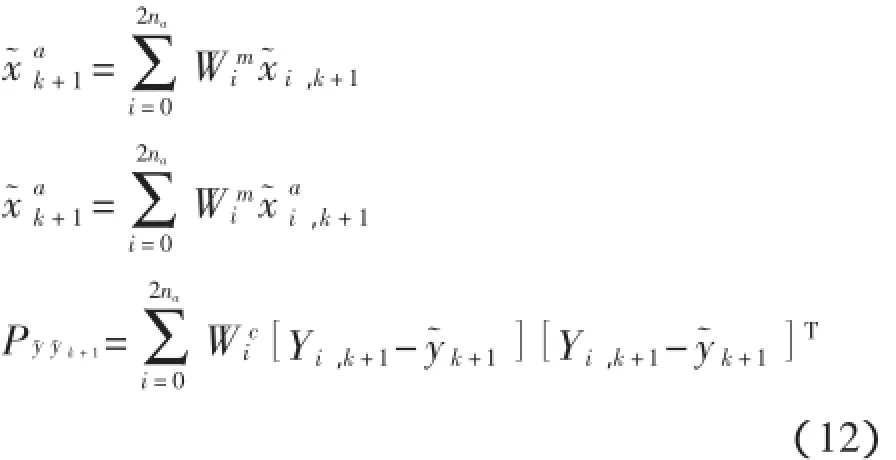
（4）測量值更新

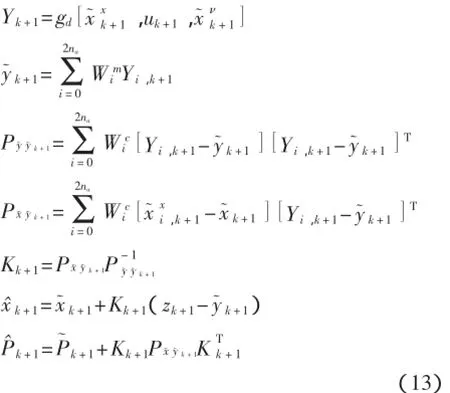
（5）循環，增加k到下一時間點，返回第（2）步并繼續。

上述UKF算法是針對一般離散時間的有非線性噪聲輸入的情況。飛行器需要連續的估計模型，根據式（14），應用數值積分法通過連續非線性方程傳遞σ點。

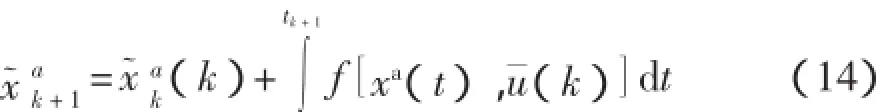
tk

2　飛行器運動參數估計模型

基于飛機的運動方程、繞質心轉動的動力學方程，進行二維分析。建立的模型進行縱向的二維估計，對固定翼飛機的升力系數、阻力系數、俯仰力矩系數進行辨識[8]。

二維飛行器運動系統狀態方程：

對應的飛行器升力系數、阻力系數、俯仰力矩系數模型：

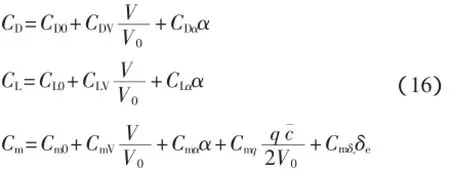
觀測方程：

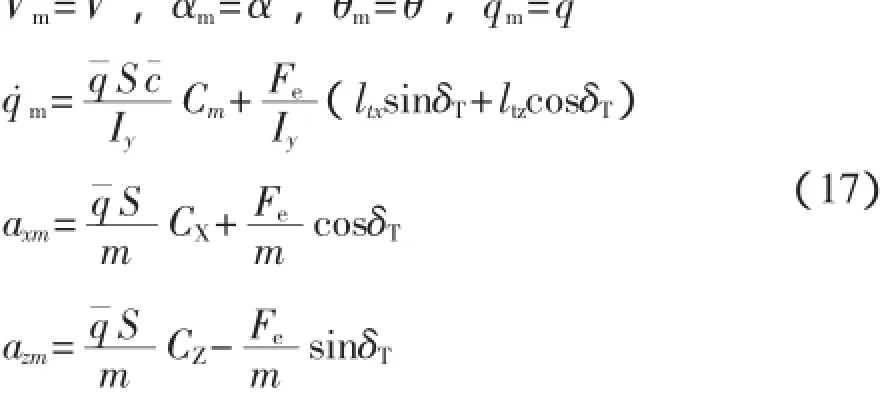
縱向氣動系數CX、垂直氣動系數CZ計算如下：

其中V真速，α仰角，θ俯仰角，q傾斜角，δe升降舵偏度，Fe推力，δT發動機傾斜角，q軈=1/2ρV2動壓，m質量，S機翼面積，c軃翼弦長度，Iy轉動慣量，ρ空氣密度。與固定軸（V，α）的變量的系統方程不但含有常見的三角函數和乘法的非線性關系，還包含與所有氣動系數相乘的動壓，動壓也是非線性參數。而且，狀態參數V的轉置導致關于α的狀態方程更加的非線性化[9]。帶辨識參數向量如下：

θ= [CD0CDVCDαCL0CLVCLαCm0CmVCmαCmqCmδe]

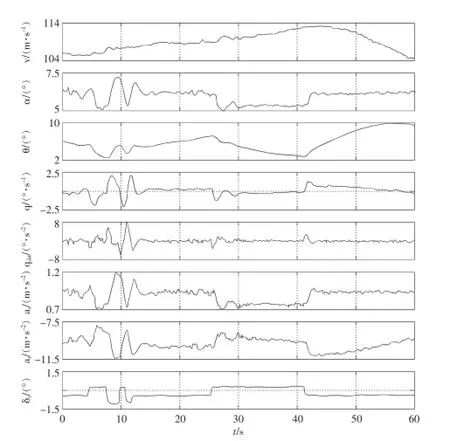
圖1　固定翼飛機氣動數據

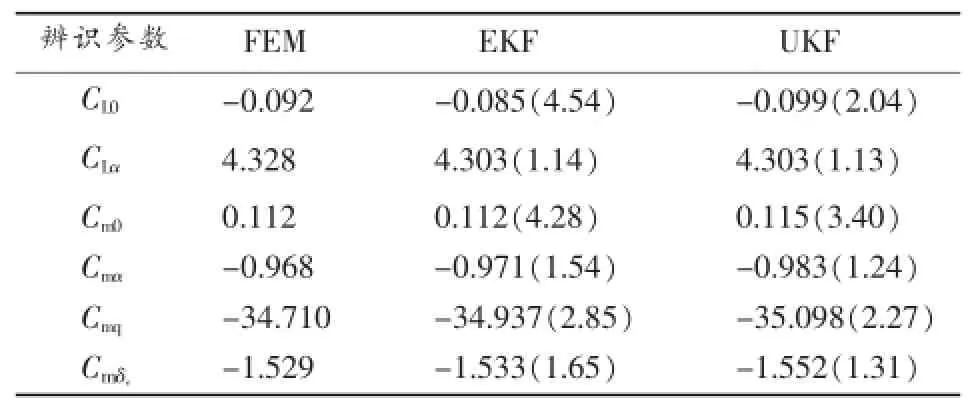
表1　氣動系數辨識結果比較

3 EKF、UKF對固定翼飛機氣動系數辨識結果比較及分析

分別通過EKF、UKF算法基于上述二維飛行器運動參數估計模型進行氣動參數辨識。已知圖1中某型固定翼飛機狀態參量數據（V、α、θ、q、q觶、ax、az、δe）。

每次辨識中，進行了1000步以上濾波。估計結果如圖2所示，比較了兩種遞歸參數估計算法的辨識性能及準確度。辨識過程顯示，EFK、UKF算法保持良好的濾波質量和收斂速度。基于EKF算法的飛行系統參數辨識保持著一貫的質量不錯的辨識結果和較低的計算成本需求。但UFK遞歸參數估計算法對收斂速度要優于EKF，UKF不但精度高，而且魯棒性能更好。

表1列出了基于EKF、UKF濾波算法的在線辨識數值結果和離線濾波器誤差法FEM離線辨識結果，并將其與標準已知氣動系數比較，括號中為辨識結果與標準系數偏差的百分比。可以看出辨識結果與已知氣動系數偏差不大，UKF辨識結果的偏差值相對EKF較小，更為精確。

對上述辨識結果進行理論分析，導致UKF濾波辨識結果優于EKF，主要由于UKF算法特點[10]：

（1）對非線性函數的概率密度分布進行近似，而EKF是對非線性函數進行近似。

（2）非線性分布統計量計算精度至少達到二階或更高階，而EKF為一階精度。

（3）不需要Jacobian矩陣計算，減少了運算量。

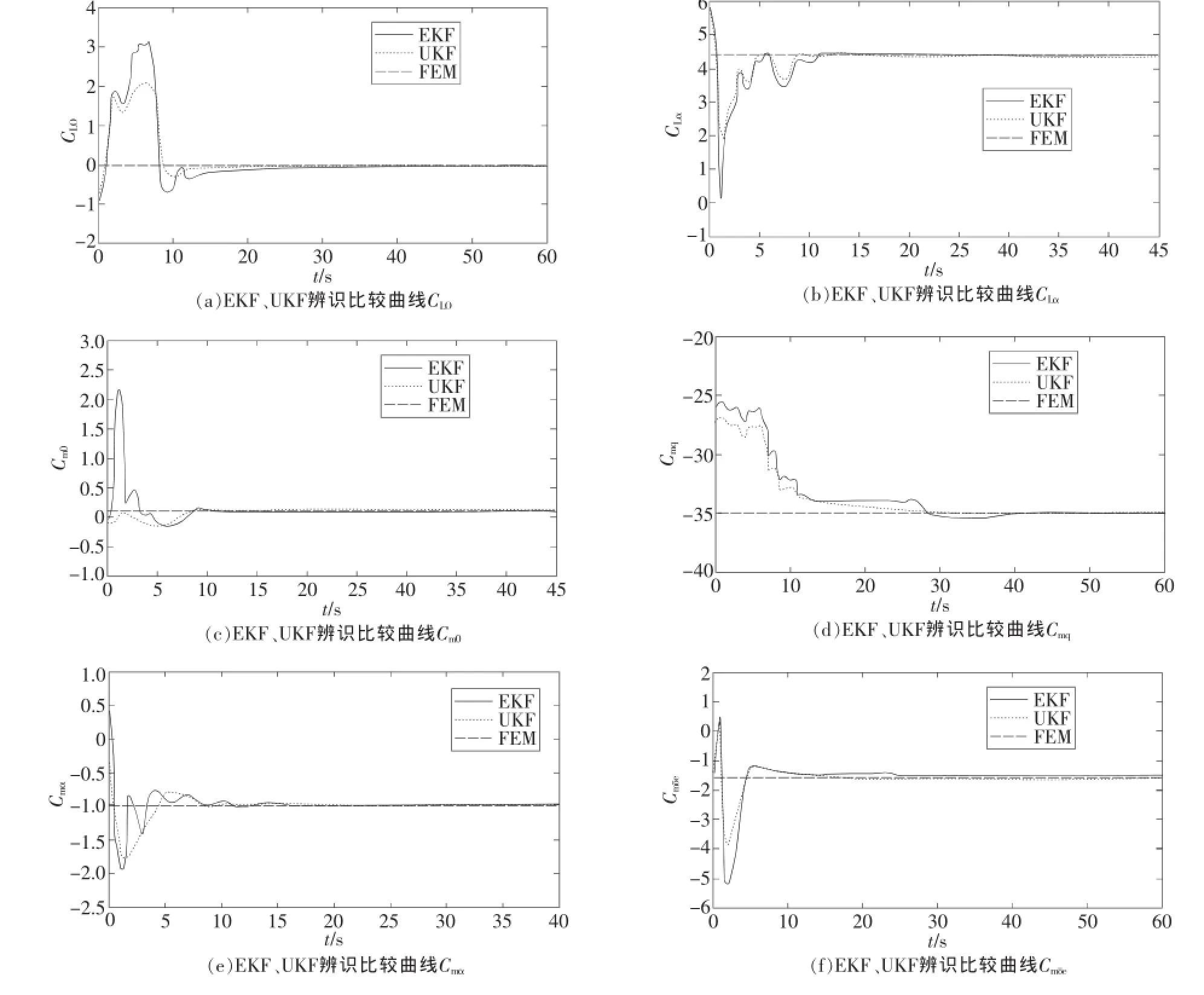
圖2　基于EKF、UKF算法氣動系數辨識曲線

（4）采用確定采樣策略，而非PF隨即采樣，避免了粒子衰退問題。

4　結束語

在本文中，通過固定翼飛機的飛行數據，對EKF算法、UFK算法的氣動參數估計性能進行了比較，分析了UKF算法在理論上相對EKF的優勢。UFK遞歸參數估計算法對收斂速度和辨識的可靠性而言，要優于EKF。目前，EKF算法的研究比較成熟，而UKF算法及其理論基礎UT變換是較新的研究領域，雖然取得了一些理論成果，如多種采樣策略及UT變換的精度證明，仍存在值得關注的方面，比如穩定性分析、采樣策略自適應研究。

參考文獻

[1] 汪清，錢煒祺，何開鋒.導彈氣動參數辨識與優化輸入設計[J] .宇航學報，2008，5（3）：97-102.

[2] Hamel P G，Jategaonkar R V. Evolution of flight vehicle system identification [J] . Journal of Aircraft，1996，33（1）：9-28.

[3] 蔡金獅.動力學系統辨識與建模[M] .北京：國防工業出版社，1991.

[4] 鄒新生，李春文.飛行器參數辨識的一種演化計算力法[J] .電光與控制，2006，13（2）：15-17.

[5] 潘泉，楊峰，葉亮.一類非線性濾波器-UKF綜述[J] .控制與決策，2005，5（2）：38-44.

[6] 楊波，秦永元，柴艷. UKF在INS/GPS直接法卡爾曼濾波中的應用[J] .傳感技術學報，2007，7（1）：127-132.

[7] 周東華，序裕庚，張鐘俊.一種帶多重次優漸消因子的擴展卡爾曼濾波器[J] .自動化學報，1991，17（6）：689-685.

[8] Garcfa V J，Walker B K. Aerodynamic parameter estimation for high performance aircraft using extend kalman filtering[J] . Journal of Guidance，Control and Dynamics，1997（6）：1257-1259.

[9] Wang X P. Aerodynamic parameter flight vehicles based on adaptive genetic[J] . Journal of Astronautics，2003（3）：303-308.

[10] Julier S J，Uhlmann J K. Unscented filtering and nonlinear estimation[J] . Proceedings of the IEEE，2004，92（3）：401-422.

Comparative study on aerodynamic parameter identification methods based on UKF, EKF

LI Zheng-nan，WANG Pei

（Military Simulation Technology Institute，Avation University of Force，Changchun 130022，China）

Abstract:In the aerospace industry，aerodynamic parameter identification is widely used in aircraft aerodynamic performance tests. As the improvement of aircraft performance，control requirements and the need for real-time online identification，demands of aerodynamic parameter identification precision and speed are getting higher and higher. In this paper，EKF，UKF and aerodynamic parameter identification model of theories in the former part were analyzed. Combining with 2D motion model of the aircraft，the performance of these two recursive parameter estimation algorithms for aerodynamic parameter estimation from flight data of fixed wing aircraft was compared，getting reference for the choice of filter algorithm in aerodynamic parameters identification.

Key words:aerodynamic parameter identification；extended Kalman filter；unscented Kalman filter；aircraft motion model

收稿日期：2013-05-02；

doi：10.11857/j.issn.1674-5124.2013.05.028

文章編號：1674-5124（2013）05-0102-05

文獻標志碼：A

中圖分類號：V211.5；TP202+.1；TP301.6；TP274+.2

作者簡介：李正楠（1990-），男，山東濰坊市人，碩士研究生，專業方向為飛行仿真。