一種遙感衛星偏流角修正的仿真分析方法

朱興鴻 邸國棟 陸春玲

（航天東方紅衛星有限公司，北京 100094）

1 引言

在遙感衛星繞地球運轉時，地球的自轉會使相機相對被攝景物的移動方向與相機運動的投影線速度方向不一致，而兩個方向的夾角稱為偏流角［1］。隨著遙感衛星成像質量要求的提高和時間延遲積分CCD（TDICCD）器件在遙感衛星上的廣泛使用，衛星偏流角的修正誤差所造成的成像系統調制傳遞函數（MTF）的衰退，已成為影響成像質量的關鍵因素之一。

國內外的相關研究在偏流角的幾何解析方面給出了比較詳細的分析。文獻［2-3］給出了基于幾何分析和公式推演進行計算的偏流角分析方法，其主要的缺點是過多地依賴于假設，如地球是個理想橢球體，衛星軌道為理想圓軌道等。各種假設會為計算結果帶來一定的偏差，一般只能作為定性的分析，無法使用這種低精度的結果來驗證星上算法的正確性和精度。此外，隨著衛星側擺、俯仰等姿態機動能力的提高，幾何分析方法推導過程復雜、精度偏低的不足就更加顯現出來。針對上述問題，本文提出了一種偏流角修正的仿真分析方法，重點解決如下3個方面的問題。

（1）通過結合仿真中的高精度模型，解決在幾何解析分析過程中對模型假設的依賴問題；

（2）從成像的物理原理出發，解決偏流角修正過程的物理意義不夠明確的問題；

（3）解決在姿態機動、橢圓軌道等特殊任務中遙感器的偏流角分析問題。

2 偏流角的產生及其修正誤差的影響

2．1 偏流角的產生

圖1（a）為星下點成像時慣性坐標系下偏流角的產生示意圖。衛星在軌道上從t1時刻的S1點運行到t2時刻的S2點過程中，衛星的星下點成像對象從t1時刻的P1點變為t2時刻的P2點，因此，在t1時刻衛星運動造成的成像點（不受地球自轉影響）相對于衛星的運動速度Vi，其大小可表示為

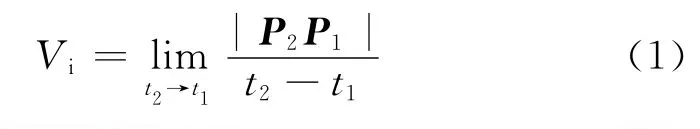
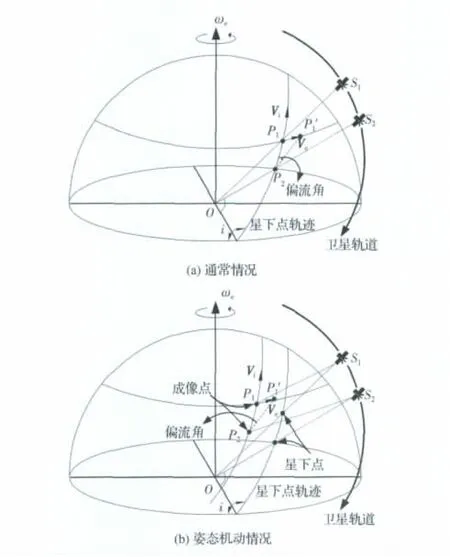
圖1 偏流角產生示意圖Fig．1 Schematic diagram of drift angle generation

由于地球自轉，地球表面的P1點存在一個牽連速度Ve，此速度使P1點在t2時刻將運行到P′1點，因此，在t1時刻的成像點相對于衛星的總運動速度就是由Ve和Vi合成的速度，合成速度與Vi的夾角就是衛星的偏流角［4］。當衛星存在姿態機動時，成像點軌跡偏離了星下點軌跡，因此衛星的偏流角應該按照此時的衛星、成像點、地球三者的運動關系進行分析，如圖1（b）所示。

2．2 偏流角修正誤差對成像質量的影響

當偏流角的修正有一定誤差時，會在TDICCD線陣方向上存在一個殘留的像移速度，因此在TDICCD積分過程中由像移引起的MTF 衰退DMTF可用式（2）計算。

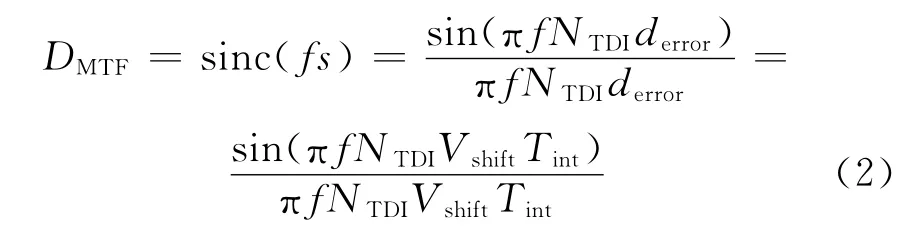
式中：f為TDICCD 線陣方向（讀出方向）的空間頻率；s為曝光時間內的像移量；NTDI為成像的TDICCD級數；derror為相鄰兩次曝光在TDICCD 線陣方向的位置誤差；Vshift為TDICCD 線陣方向像移速度；Tint為積分時間。

通過對TDICCD 相機成像過程進行空間建模［5］，獲得不同積分級數下偏流角修正誤差造成的MTF衰減如圖2所示。可以看出，偏流角的高精度修正對提高成像質量至關重要［6］。

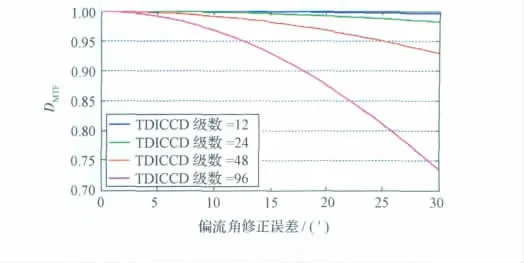
圖2 不同積分級數下的偏流角修正誤差造成的MTF衰減Fig．2 MTF degradation caused by drift angle adjustment error at different integration levels

3 偏流角修正的仿真分析

3．1 偏流角修正物理過程分析

TDICCD 相機是一種具有多重級數延時積分功能的線陣CCD 相機。其工作原理是：當相機隨衛星向前運動時，對地面同一目標進行多次曝光成像，采用同步多級積分來增加成像積分時長，以提高接收能量和信噪比。由于TDICCD 相機在低照度情況下具有良好的成像性能，近年來被廣泛應用于新一代高分辨率遙感衛星成像［7-8］。

對于一個TDICCD 器件，成像中偏流角影響及其修正的原理如圖3所示。修正的目的就是通過衛星的姿態調整，將CCD 的方向修正到與成像點相對于CCD 運動速度完全垂直，消除CCD 成像過程中的橫向像移，從而使圖像在TDICCD 的多次積分中始終維持圖像相位的穩定性［9］，這個修正的角度就定義為偏流角修正。需要注意的是，圖3中的角度和矢量間的關系都是在CCD 焦平面上定義的，因此，雖然偏流角可以用來表征遙感衛星成像目標的運動特點，但是此偏流角只能直接作為星下點成像偏流角修正。衛星側擺時成像點的速度并不在CCD 的焦平面上，要首先進行投影，才能通過其與CCD 間的關系得到偏流角修正，如圖4所示。

圖3 成像過程中偏流角影響及其修正原理Fig．3 Principle of drift angle influence and relative adjustment in imaging

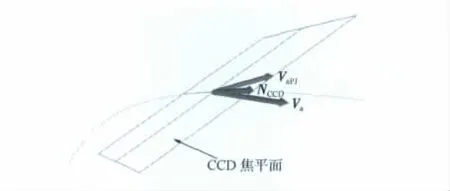
圖4 偏流角修正的投影關系示意圖Fig．4 Schematic diagram of projection on drift angle adjustment

圖4中的平面為CCD焦平面，Va為分析偏流角時成像點相對于衛星的運動速度，NCCD為TDICCD的法線方向，VaPJ為Va在CCD 成像平面上的投影。根據修正的目的，通過修正使NCCD與VaPJ重合，這樣，NCCD與VaPJ間的夾角即為實際的偏流角修正角度。

3．2 仿真方法及流程

本文提出的仿真方法，從上文分析的成像物理原理出發，解決偏流角修正的計算問題。仿真以成像對象的運動狀態為基礎，分別獲得其在慣性坐標系下由于地球自轉和衛星運動產生的相對于衛星的運動速度，進一步分析成像對象相對于CCD 的運動關系，并以消除CCD 橫向像移為基本出發點來分析偏流角修正。

仿真過程中使用了STK 軟件與MATLAB 軟件，通過MATLAB 軟件控制STK 軟件進行交互，并對獲取的STK 軟件數據進行分析，仿真交互及分析過程如圖5所示。

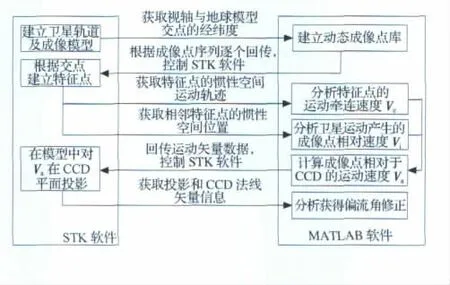
圖5 仿真交互及分析流程圖Fig．5 Flow chart on simulation interaction and analysis

4 示例

4．1 650km 太陽同步軌道衛星

在仿真中使用了STK 軟件作為軌道分析軟件，軟件中已經包含了高精度的地球模型。為了能夠更好地模擬真實衛星的成像特性，在仿真場景中選取了軌道高度為650km 的太陽同步軌道，軌道降交點地方時選擇可見光衛星成像條件較好的10：30，衛星場景如圖6所示。示例中衛星具有側擺機動能力，星上僅配置一臺TDICCD 相機，取衛星本體坐標系的XOY平面為CCD 的焦平面。衛星對星下點成像以及進行側擺機動（＋15°、＋25°和＋35°）時，通過仿真獲得偏流角和偏流角修正隨緯度變化的關系，如圖7所示。

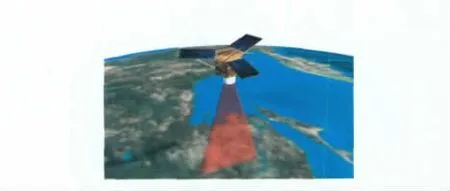
圖6 運行在650km 高太陽同步軌道衛星的仿真場景Fig．6 Simulation scenario of satellite in 650km SSO

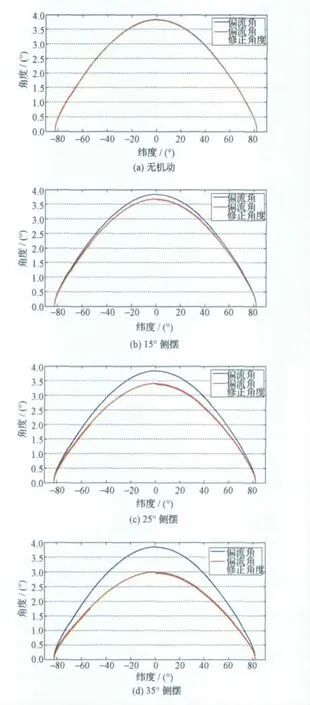
圖7 650km 高太陽同步軌道衛星的偏流角和偏流角修正仿真結果Fig．7 Simulation results of drift angle and drift angle adjustment for satellite in 650km SSO

從圖7可以看出：當衛星對星下點成像時（無機動），偏流角和偏流角修正角度兩者的曲線重合；衛星進行姿態機動，會造成成像點運動矢量與衛星CCD 焦平面的夾角關系發生變化，因此在進行投影時就會直接影響到偏流角修正，并且這種影響隨著衛星星下點緯度的減小而增加，在赤道位置達到最大。因此，在衛星進行姿態機動時，不能使用星下點的偏流角直接進行修正，否則形成的偏流角修正誤差會影響成像質量，特別是在大角度側擺機動時，此修正誤差將使系統MTF大幅度衰退。

4．2 仿真方法在復雜任務中的應用

本文提出的仿真方法是基于物理成像原理進行分析的，因此還能在眾多復雜任務中使用，以一顆臨界傾角［10］太陽同步大橢圓軌道的衛星（見圖8）為例。在模型中設置衛星的軌道及姿態參數后，使用與4．1節相同的交互仿真方法，即可仿真獲得偏流角以及偏流角的分析數據，在星下點成像（無機動）和側擺25°成像時的結果如圖9所示。此外，該仿真方法還可以在相機偏場安裝、姿態機動過程成像等多種復雜任務環境中分析系統的偏流角修正，從而在衛星系統任務分析、星上偏流角修正算法驗證、在軌誤差分析補償方面發揮重要作用。

圖8 臨界傾角太陽同步軌道衛星仿真場景Fig．8 Simulation scenario of critical inclination SSO satellite

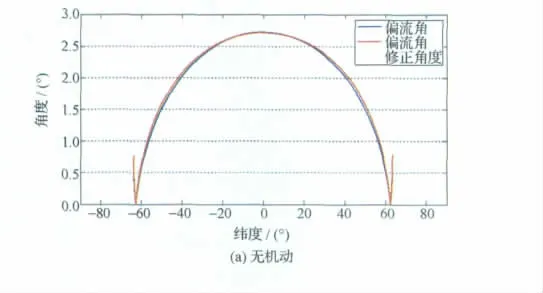
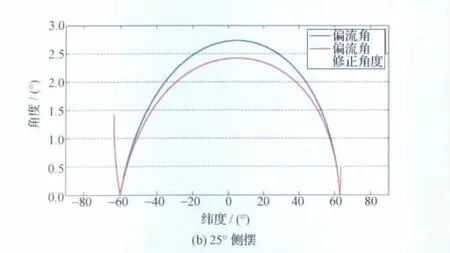
圖9 臨界傾角太陽同步軌道衛星的偏流角和偏流角修正仿真結果Fig．9 Simulation results of drift angle and drift angle adjustment for satellite in critical inclination SSO

5 結束語

本文在從運動機理分析偏流角和偏流角修正的基礎上，提出了一種基于成像點慣性運動狀態、使用MATLAB和STK 軟件交互進行仿真的方法，并結合2種衛星場景給出了偏流角的分析結果。基于仿真分析結果，可以對星上使用的偏流角修正算法進行驗證評估，以完善鏈路成像質量預估模型；也可以進一步優化星上算法，為提高衛星在軌成像質量提供支持。在本文的仿真場景中，沒有將遙感器的安裝角度、安裝偏差等系統初始狀態加入模型，而在實際使用中需要綜合考慮，在分析視軸偏流角的基礎上研究全視場偏流角偏差的影響。如果要獲得更高的精度，還應結合地球的數字高程模型（DEM）。這些也將是后續研究的重點，以得到與實際衛星狀態更接近的系統分析結果，為提高遙感衛星的成像質量奠定基礎。

（References）

［1］Longo J，Stern F．Effects of drift angle on model ship flow［J］．Experiments in Fluids，2002，32（5）：558-569

［2］袁孝康．星載TDI-CCD 推掃相機的偏流角計算與補償［J］．上海航天，2006，23（6）：10-13

Yuan Xiaokang．Calculation and compensation for the deviant angle of satellite borne TDI-CCD push scan camera［J］．Aerospace Shanghai，2006，23（6）：10-13 （in Chinese）

［3］樊超，李英才，易紅偉．空間相機中的偏流角分析［J］．紅外與激光工程，2006，35（10）：216-220

Fan Chao，Li Yingcai，Yi Hongwei．Analysis of drift angle on space camera［J］．Infrared and Laser Engineering，2006，35（10）：216-220（in Chinese）

［4］Hu Jun，Cao Xiaotao，Wang Dong，et al．Dynamic closed-loop test for real-time drift angle adjustment of space camera on the Earth［C］／／Proceedings of 5th International Symposium on Advanced Optical Manufacturing and Testing Technologies：Optical Test and Measurement Technology and Equipment．Washington D．C．：SPIE，2010：76560Z

［5］邸國棟，朱興鴻．TDICCD 相機安裝精度對系統調制傳遞傳函的影響．［J］航天器工程，2012，21（4）：59-62

Di Guodong，Zhu Xinghong．Analysis on system MTF degradation effects of assembly precision of TDICCD camera［J］．Spacecraft Engineering，2012，21（4）：59-62（in Chinese）

［6］楊秀彬，賀小軍，張劉．偏流角誤差對TDI CCD 相機成像的影響與仿真［J］．光電工程，2008，35（11）：45-50

Yang Xiubin，He Xiaojun，Zhang Liu．Effect and simulation of the deviant angle error on TDI CCD cameras image［J］．Opto-Electronic Engineering，2008，35（11）：45-50（in Chinese）

［7］佟首峰，李德志，郝志航．高分辨力TDI-CCD 遙感相機的特性分析［J］．光電工程，2001，28（4）：64-67

Tong Shoufeng，Li Dezhi，Hao Zhihang．Analysis on the characteristics of TDI-CCD high-resolution camera for remote sensing［J］．Opto-Electronic Engineering，2001，28（4）：64-67（in Chinese）

［8］楊秉新．TDICCD 在航天遙感器中的應用［J］．航天返回與遙感，1997，18（3）：15-18

Yang Bingxin．Applications of TDICCD in space remote sensors［J］．Spacecraft Recovery ＆ Remote Sensing，1997，18（3）：15-18（in Chinese）

［9］李友一．空間相機中的偏流角控制［J］．光學精密工程，2002，10（4）：402-406

Li Youyi．Drift angle control for space cameras［J］．Optics and Precision Engineering，2002，10（4）：402-406（in Chinese）

［10］章仁為．衛星軌道姿態動力學與控制［M］．北京：北京航空航天大學出版社，1998：24

Zhang Renwei．Satellite orbit and attitude dynamics and control［M］．Beijing：Beihang University Press，1998：24（in Chinese）