在幾何教學中培養學生創新能力的思考
摘 要:在新課程理念下,如何探索一條適合學生主動發展、有利于學生創新精神、實踐能力、合作品質培養的教學方式,成為在新課改中教育工作者面臨的主要課題。課程改革后的數學課堂應設計富有探索性、挑戰性的問題,讓學生通過自主探索和合作交流,培養其主動探索、敢于實踐、善于發現的科學精神。
關鍵詞:創新能力;幾何圖形;學生主動發展;培養學生;教學情境;自主探索;主動探索;創新思維
幾何是由概念、公理、定理所組成的,具有嚴密邏輯體系的科學,它具有高度的抽象性、嚴密的邏輯性和應用的廣泛性等特點。在中學階段隨著學生知識量的增加,學生的抽象思維能力開始由經驗型向理論型水平轉化。
一、培養學生的興趣,學習的過程是伴隨著情感的活動
興趣是最好的老師,學生只有強烈的求知欲才能在學習中表現出積極性和主動性,培養學生學習幾何興趣的方法較多。如:講有關幾何的發展史的故事,組織競賽,組織課外小組,自編自評試卷等。培養興趣是為創新打基礎。如:在講“軸對稱圖形”這一節時,拿出世界著名對稱建筑圖案,使學生對對稱美產生興趣,進而研究軸對稱圖形。興趣促進創新,創新過程也會產生無窮無盡的興趣。
二、培養學生的觀察能力
觀察是人們對直觀現象的直接認識是有目的,有計劃的,它為人們進一步實踐提供豐富的感性材料。幾何圖形來自我們的身邊,來源于我們所熟悉的實物,如:學生通過觀察活動鐵門,可以幫助學生理解四邊形的不穩定性,進而去研究四邊形的有關知識,教師在教學中多給學生提供機會,使學生養成愛觀察圖形的好習慣。
三、培養學生的動手能力
動手就是培養學生技能技巧,促進知識轉化的能力,它可以鍛煉學生的思維,使學生更具有創造力。如:學習三角形內角和定理時,讓每個學生把三角形的兩個角剪下來,拼在第三個角的頂點處,得出三角形內角和是180度,這樣不僅得出了結論,又獲得了證明方法。在講直線與圓的位置關系時,學生把直線與圓作相對運動就得到直線與圓的位置關系,這樣的動手實踐,學生自己發現了定理和新知識,比教師講授更容易接受,并激發了學生的學習熱情,堅定了他們創造發明的信心。
四、培養學生提出問題的能力
敢于提出問題和善于提出問題,是探索未知世界,一切具有發明創造人的共同特性,正如愛因斯坦所說:“提出一個問題往往比解決一個問題更重要,因為解決問題也許僅是一個數學上或實驗上的技能而已,而提出問題,新的可能性,從新的角度去看問題,卻需要有創造性的想力,而且標志著科學的真正進步。”在教學中引導學生提出問題的方法很多。如:類比提問,聯想提問等方法。如:講完四邊形的知識后,教師引導學生提出一個角是直角的平行四邊形和一組鄰邊相等的平行四邊形,它們的圖形應該是什么形狀的呢?從而引出平行四邊形,促使學生去探索特殊平行四邊形的性質。
五、培養學生一題多解的能力
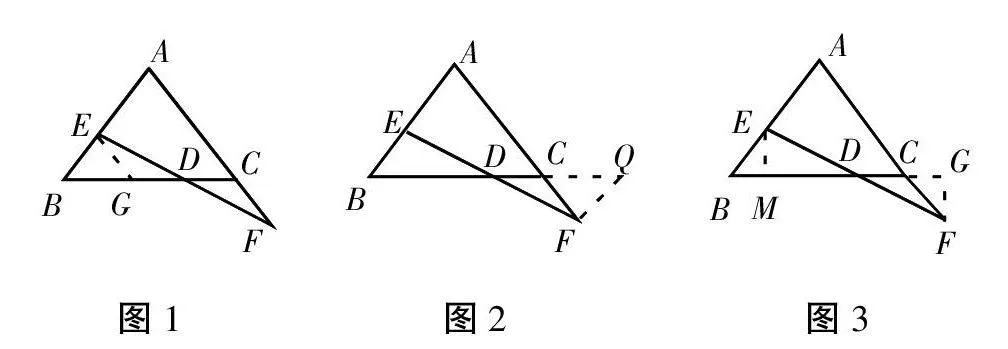
學習知識的最終目的是解決問題,在解決過程中找出新的思路,或在同一思路中提出新的論證方法,或用各種知識的巧妙的連接去解決其他學科和生活實踐中遇到的各種問題,如在圖1中AB=AC,EF交AB于E,交AC的延長線于F,且BE=CF,求證:DE=DF。
證法一,如圖1,過E作EG//AC,交BC于G構成新的三角形。
證法二,如圖2,過F作FQ//AB,交BC延長線于Q,以△DEB為標準。
證法三,如圖3,過E作EM⊥BC,交BC于M,過F作FG⊥BC,交BC的延長線于G,重新構造兩個新的全等三角形。
這道題的三種方法,從不同角度去引輔助線,證明的方法不同,從而培養學生的解題能力。
總之,在以往教學中,偏重于學生的邏輯思維訓練,而忽略了學生的發散創新思維能力,忽略了教會學生大膽地進行不嚴格的猜想,聯想和和情推理,所以在今后的教學中更應該注重培養學生的直覺思維能力和發散創新思維能力。所以隨著現代科技的發展,培養學生的開拓性,創新意識更是勢在必行。
(作者單位 吉林省遼源市農村實驗中學)

