從《圓和圓的位置關系》的教學談如何挖掘學生自主學習的內驅力

摘 要：教學活動是師生的雙邊活動，以學生為主體、教師為主導。要發揮學生的主動性，讓學生自主學習，教師要營造氛圍設置情境，開啟學生的求知欲，激發學生興趣，調動他們學習的積極性。

關鍵詞：內驅力；圓和圓的位置關系；自主學習

以《圓和圓的位置關系》的教學為例，談談我對挖掘學生自主學習的內驅力的認識。

一、問題的提出和指導

在講《圓和圓的位置關系》時，我設計以下問題系列實現教學目標。

1.問題一：同學們見過月食嗎？

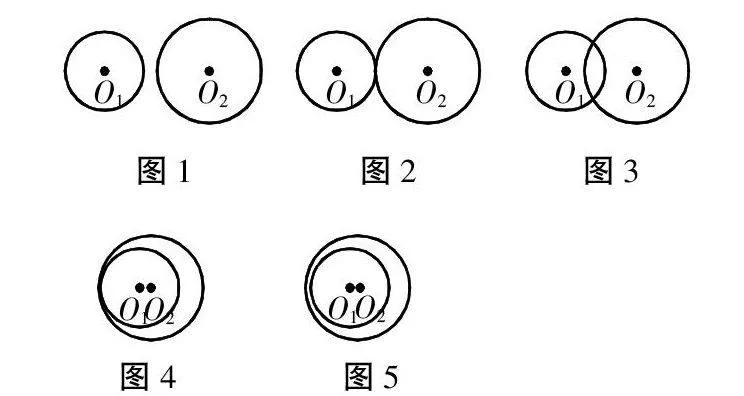
問題一提出，學生的思維一下子活躍起來。于是我又請一個學生上來演示月食過程。學生的注意力被吸引過來，經過指點又注意到兩圓公共點變化的情況。最后在屏幕上打出兩圓各種不同位置關系的圖形。

這樣以學生熟悉的自然現象為背景，在演示物體相對運動的過程中建立數學模型，提示概念本質，既能提高學生研究的興趣，又能通過演示形成平面內兩圓不同位置關系的感性認識，為下面的學習做好心理上的準備。

2.問題二：根據以上觀察，能否制定一個適當的標準，把以上各種關系分為幾類？經過短暫思考，有學生甲回答：兩圓公共點一共有三種可能，可以按兩圓公共點的個數來進行分類。

（1）若兩圓沒有公共點叫相離；

（2）若兩圓只有一個公共點叫相切；

（3）若兩圓有兩個公共點叫相交。

學生從觀察現象到透過現象看本質，是從感性認識到理性認識的一個飛躍。由于已學習過直線和圓的位置關系的劃分，盡管還沒有給出圖中兩圓位置關系的定義，但由于知識的遷移作用，學生仍憑經驗概括出了上面三種位置關系，我對他們的回答給予高度賞識和鼓勵，并為之而歡呼。學生的積極性被調動起來。

3.問題三：討論上述劃分方法的正確性。介紹相切兩圓的連心線的性質。

經過這一段討論，使學生領會：（1）由于過三點不能有兩個圓，故兩圓公共點的個數最多有兩個。類比“直線與圓的位置關系”的劃分，這種劃分是合理可行的。（2）連心線是兩圓的公共對稱軸，相切兩圓的連心線必過切點。

把“圓與圓的位置關系”與“直線與圓的位置關系”在分類方法上進行類比，既有利于學習新知識，又有助于復習舊知識，便于學生在原有知識的基礎上逐步構建出兩圓位置關系的定義。

了解了連心線的性質，便為下面的學習做了準備。

4.問題四：大家知道，直線與圓的三種位置中，“連心距”（圓心到直線的距離）和圓的半徑之間有明確的數量關系，那么在你們劃分的三種“圓與圓的位置關系”中，圓心距和兩圓半徑之間是否分別具有某種對應的數量關系呢？

學生通過對圖形的觀察容易發現各種圖形下的圓心距和半徑的對應數量關系，同時又發現了新的問題：在相切（相離）的兩種圖形中，圓心距與兩圓半徑之間有著截然不同的數量關系。即三種位置關系對應著五種數量關系：不像直線與圓那樣，位置關系與數量關系一一對應。劃分為三種位置關系顯然還不夠完善。學生提出應該修改標準，把相切（離）的兩種情形區別開來，以求位置關系與數量關系之間的一一對應。

5.問題五：如何修正學生甲的定義，實現兩種標準的統一？

學生通過上面的討論已經體會到：從d與R+r和R-r的關系

來看，兩圓位置關系分為五類更合適。于是反過來討論如何修改甲同學的劃分標準，使兩種方法能達成一致。經過討論，結合兩圓位置特征修改并給出兩圓位置關系的定義。

運用兩種標準下劃分結果不統一的矛盾，誘發了學生的求知欲，激發了學生的探索精神，促使學生在思維不斷發展的過程中逐步完成新知識的構建，從而把知識的外部交流形式內化成學生的心理接受過程，學生不再是知識的奴隸，而是知識的主人。

6.問題六：系統歸納各種位置關系與數量關系。

在問題五的研究過程中，逐步系統歸納出五種位置關系與五種數量關系之間的一一對應。

位置關系數量關系

兩圓外離d>R+r

兩圓外切d=R+r

兩圓相交R-r

兩圓內切d=R-r

兩圓內含d

現實世界由空間形式和數量關系構成，數能解形，形能助數。問題六的研究成果是本節課的目標指向。它以數形結合為指導，以分類討論為手段，把五種位置關系與五種數量關系建立起一一對應的聯系，體現了數學中的“量變”（數量關系）、“質變”（位置關系）規律，實現了數形之間的相互轉換。

二、本節課的指導思想

變學生被動吸收知識的過程為在原有基礎上主動構建（知識建構、方法建構、思想建構）的過程。結合生活實際，從月食演變的過程出發，設計出一系列的動態思維過程。既提示概念的本質，又培養出學生數學思維的品質。培養學生建構新知識、新方法、新思想的意識，提高學生運用數學思想研究問題、解決問題的能力。

三、本節課對學生自主學習方面的內驅力特征的挖掘

1.思維的發散性

青少年遇到問題善于思考，在思維上的特點是由一點想開去，產生廣泛的聯想、想象，想到一個問題的許多方面，也能以一個問題想到另一個問題進而把頭腦中貯存的信息資料都調動起來。由月食的演變過程進而聯想到圓與圓的位置關系。本節課的引入設計正是證明了這一點。

2.具有集合思維能力

有了廣泛的發散以后，還要依靠集合思維對發散思維產生的許多方法、觀點、方案、想象進行比較、整理、推理、選擇，從中確定出最佳方案、最佳方法、最佳觀點。學生自主學習的內驅力強烈與否，也表現在該學生的集合思維能力的高低，因為這得完全靠自己動腦思維，重新組裝知識，這是一個高能力階段。本節課正是由月食演變過程先在學生頭腦中形成平面內兩圓不同位置關系的感性認識，根據已學過的直線與圓的位置關系的劃分方法，聯想到按公共點的個數來劃分圓與圓的位置關系。再引導學生觀察圖形，通過位置關系和數量關系的討論，激化出數學中的矛盾，促使學生對上面的劃分標準進行修改，最后歸納出五種位置關系與五種數量關系之間的一一對應。

3.高度的自主性體現了“自我充分發展”的需要

一個人總是要根據環境條件和個體生活發展的新需要，引起某種創造的動機，表現出創造的意向和愿望。在《在圓與圓的位置關系》的教學中，學生正是通過自我實現，將自己的數學稟賦、才能充分發揮，實現個人的理想認識。在這種具有自主性和獨立性的“自我創造”中，發揮原型啟發的作用，豁然貫通，通過聯想找到解決問題的新方案，促進自己的不斷發現，從而解決關鍵性的問題。

隨著社會的發展，對教育的要求越來越高。要培養適合時代需要的人才，靠傳統的教育已力不從心了。一旦學生有了自主學習的意識，教師要為其創造自主學習的空間，學生學習的主體內在因素就會發生變化，就能把“要我學”變成“我要學”，從而積極配合老師，形成獨立意識，提高學習的效果，就能變厭學為樂學，變死學為善學，自覺培養良好的學習品質和勇于探索、勇于創新的精神，成為駕馭知識的主人。

（作者單位 江西省石城縣贛源中學）