改進的小波神經網絡在變壓器故障診斷中的應用*

李曉靜，李 杰

(濟源職業技術學院，河南濟源459000)

長期以來，國內外一直對變壓器故障診斷技術的研究和開發給予高度的重視，經過數十年的研究和探索，形成了一大批行之有效的診斷方法。而傳統意義上由特征氣體濃度信息直接或通過簡單的計算比值判斷故障類型的方法，在實際應用過程中由于知識獲取困難等一系列問題的存在，導致直接應用的效果非常不理想［1］。尤其是需要根據各種參數做出正確的判斷，更是要求相關故障診斷人員必須有堅實的理論基礎和豐富的運行維護經驗。由于單一的故障檢測方法所存在的局限性，因此，綜合運用多種智能方法來對變壓器故障進行診斷和處理，已經成為當前階段的變壓器故障診斷的主流趨勢［2］。

在本文的研究中，集中采用了小波變換方法和神經網絡方法，通過對兩者的綜合應用來構建一個以小波神經網絡為主要內容的變壓器故障診斷算法模型，有效地利用了小波變換方法的局部優化特征，同時也結合神經網絡的自學習功能，實驗證明，該算法不僅具有較強的逼近、容錯能力，而且提高了局部搜索能力，收斂速度等方面的性能得到較大提升。

1 神經網絡算法

作為一種典型的非線性動力學系統，人工神經網絡在多個領域中的應用都取得了較好的效果。與傳統的基于算法的辨識方法相比較，基于神經網絡的辨識具有以下幾個特點:(1)不要求建立實際系統的辨識格式，即可省去系統結構建模這一步;(2)可以對本質非線性系統進行辨識;(3)辨識的收斂速度不依賴于待辨識系統的維數，只與神經網絡本身及其所采用的學習算法有關;(4)神經網絡具有大量連接，其連接權的權值在辨識中對應于模型參數，通過調節這些參數可使網絡輸出逼近系統輸出;(5)神經網絡作為實際系統的辨識模型，實際上也是系統的一個物理實現，可以用于在線控制。正是由于這些特點，神經網絡算法在故障診斷過程中的應用才顯得尤為重要。誤差反向傳播BP(Back Propagation)作為一種較為強大的全局逼近網絡，其學習方法的應用主要是通過對多層前饋式輸出模式的應用來實現誤差逐層回饋的訓練方法，尤其是3層BP神經網絡，更是能夠有效地對任意精度逼近非線性函數，因此在解決實際工程中的非線性問題時得到廣泛的應用。

雖然BP算法作為目前最為常見的一種人工神經網絡算法，但是由于在實際的運算過程中整體收斂速度相對較慢，同時非常容易導致局部極小點的出現，因此出現了大量的改進算法［3-4］。雖然這些改進算法有效的提升了BP算法的整體有效性，但是仍然不能夠完全的規避該算法原有的種種劣勢。在實際應用中，較多采用基于Sigmoid激勵函數的BP神經網絡，Sigmoid激勵函數為全局函數，存在嚴重重疊，所以這種網絡存在較易陷入局部極小，收斂速度慢，抗噪聲能力差的缺點。而且一些改進的BP算法同樣無法真正地解決這一問題。

2 小波神經網絡算法

2.1 算法描述

小波變換相對于傅里葉變換來說具有一定的優勢。在實際的應用過程中，小波變換主要是通過對尺度分析過程中的伸縮和平移來確定型號的局部信息。通過小波變換的方式來對本文所研究的神經網絡算法進一步彌補，能夠從本質上提升神經算法的整體學習能力，并在實際應用過程中起到足夠的優化作用，保證其整體的應用效果。在本文中所重點研究的小波神經網絡系統，實際上就是一種以小波變換算法為基礎的改進型神經網絡系統，兼具兩者的優點，并在性能上有著明顯的突破。客觀上來說，根據小波分析理論來對神經網絡的整體結構加以處理和分析，不僅僅能夠有效的提升其整體的學習能力，同樣也能夠最大限度的提升其整體收斂速度。

小波變換算法在具體的應用過程中主要應該包括如下幾個方面［5-6］。

(1)初始化基本參數為a，并對具體運算過程中的重點數據結構平移系數用b表示，同樣，根據具體的計算需求，我們用Wnh和Whm來分別表示輸入層與中間層之間的連接權值和隱含層與輸出層之間連接權值，在這一過程中，我們可以將學習率記為β(β＞0)，并通過對該算法一般規律的把握為其賦予初始值，當然，在賦值時我們有必要設定輸入權值樣本計數器為count(count=1);

(2)設定輸入學習樣本記為Xn，相應的期望輸出記為Tm;

(3)通過對具體變量數據的輸入，可以得出如下所示的算式:

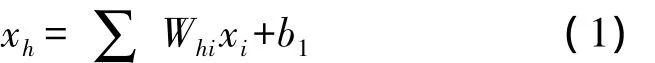
通過上述處理之后，我們需要通過中間層的小波函數來計算輸出方程，計算方法如下:

利用Wnh來對所研究的輸出層不同要素之間的整體輸出值的計算結果，我們可以通過一定的簡化計算為如下算法:

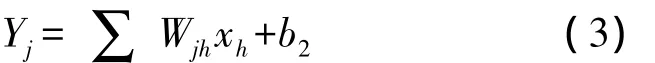
(4)根據實際的應用計算需求用期望輸出Tm并結合相應具體網絡的實際輸出來完成對所研究的輸出層誤差E(W)的初步計算;

(5)count=count+1，通過簡單的計算得出count的值，將其和p做出對比分析，如果對比結果中，count＜p為真，那么繼續進行步驟2的實現。反之則需要對E(W)進行計算，并對參數做出相應的修改和恢復;

(6)通過上述流程之后，我們需要將E(W)的具體數值和預定的ε(ε＞0)進行對比分析，判斷其真假，以此為依據考慮重復操作還是直接得出結果。

2.2 算法改進

正如上文中所論述的，該算法在實際的應用過程中具有非常明顯的不足之處，因此需要對其進行改進。在本文的研究中，如果采用傳統意義上的最速下降法的傳統網絡尋優算法來對上述數據進行處理，那么雖然能夠更為簡單明了的完成整個訓練過程，但是對于神經網絡的整體收斂速度的提升是沒有意義的［7-8］。這種情況下，動量批處理小波神經網絡算法的應用就有了其客觀需求，通過如此改進，不僅僅能夠有效的提高訓練速度，并對學習路徑做出平滑處理，同樣能夠有效的提升整體的數據處理準確度［9］。與此同時，在這一過程中為了有效規避訓練過程中可能出現的發散問題，可以通過加權求和方法的應用來加以解決。實際上，通過該方法對網絡隱含層小波結點的輸出進行計算得出結果之后，再結合SIGMOID激勵函數變化得到最終的網絡輸出。在這一過程中，通過對參數的學習率的調整，就能夠完美的解決傳統算法中出現局部最小值的問題。該方法在實踐中的大量應用，已經得到了廣泛的證明。

上述算法在權值調整過程中具體算法如下:

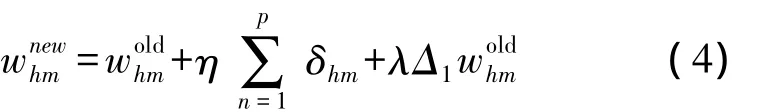
其中和分別表示權值調整前后的連接權值情況，而在上述算式中代表的含義為動量項。

伸縮因子調整:

除此之外，在上述計算過程中，網絡輸入層和隱含層權值調整方法類似于式(4)，而平移因子在具體的應用過程中，調整方法基本等同于式(5)。

3 實驗仿真和分析

3.1 仿真環境

基于WINDOWS XP的工作平臺，設定硬件環境為CPU:P43.0，內存 4 GHz，硬盤 1 T，結合 SQL Server 2000數據庫和Matlab 7.0作為仿真環境，對本文所研究的算法進行仿真實驗。

3.2 實驗參數及數據

本文所進行的試驗驗證數據來源于某變壓器廠，第1步，從所收集的200個歷史故障中，隨機抽取二分之一的樣本數據進行訓練，并用同樣的方法抽取總量的二分之一個樣本進行測試。第二步，通過這一樣本為主要輸入數據，構造出一個輸入層為5，輸出層為5，隱含層數量為10的神經網絡，設定輸入變量為Xi(i=1，2，…，5)，分別代表氣體 H2、CH4、C2H6、C2H4 和C2H2的含量在總氣體含量中所占的百分比;設定不同的輸出故障類型為Yi(i=1，2，…，5)。

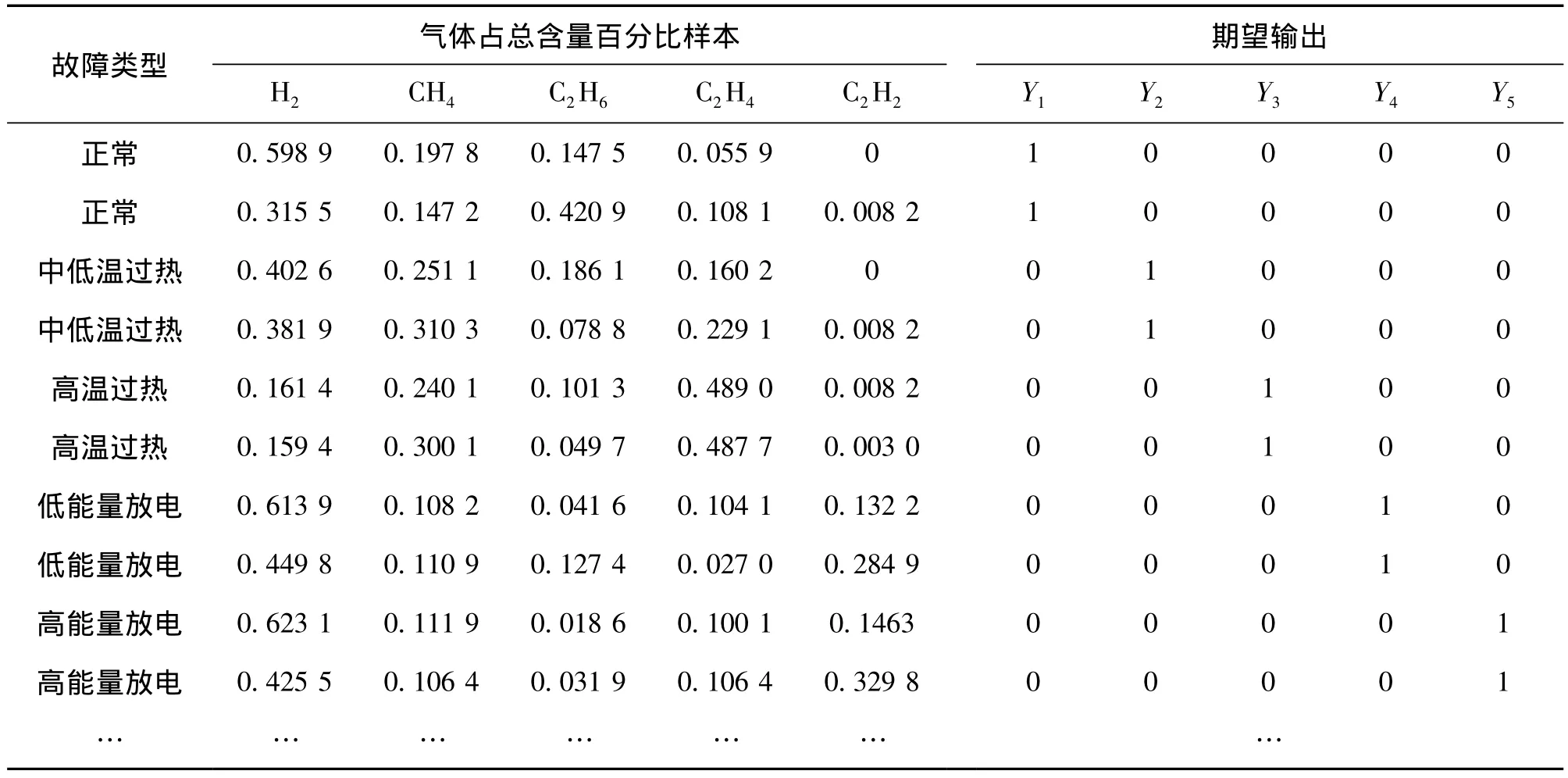
表1 訓練樣本

3.3 仿真結果及分析

通過對上述樣本模型的兩種算法的應用對比分析，可以得到如圖1所示的訓練誤差曲線。

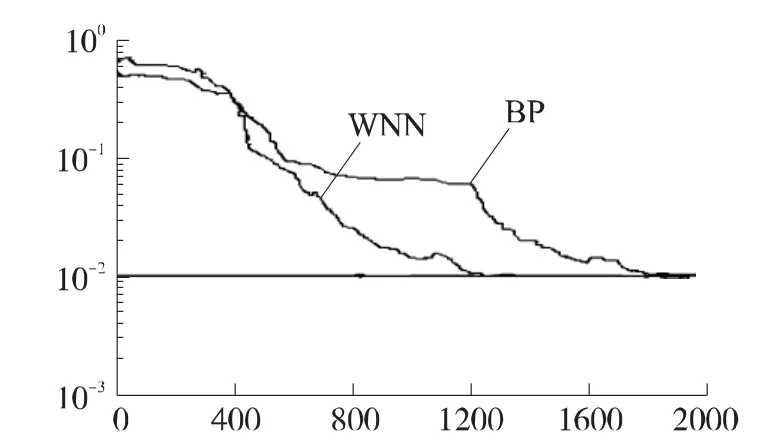
圖1 訓練誤差曲線

通過對上圖的簡單分析我們可以知道，本文所研究的改進的小波神經網絡算法在收斂速度上具有明顯的優勢。為了更好的驗證這一特點，我們分別對兩種算法進行了一百次的樣本對比訓練分析，并對其收斂速度的具體步驟進行求解。

在對100個測試樣本進行診斷模型的故障檢測中，本文所研究的重點內容小波神經網絡(WNN)的符合率高達95%;而與之相對應的傳統意義上的BP神經網絡算法符合率僅有83%;這種情況的客觀存在，足以說明在變壓器故障診斷過程中，相對于傳統算法來說WNN網絡模型優勢顯著。

4 結束語

本文重點研究了小波變換和人工神經網絡系統在變壓器故障診斷中的應用，并通過數據分析的方法強調了該算法的優勢特征，提了加動量批處理小波神經網絡算法，并通過對本文所研究的神經網絡模型構造過程中的應用，通過仿真實驗的方式對其實際性能做出了驗證和測試。實驗結果表明，相對于傳統意義上的BP網絡算法來說，本文所研究的小波神經網絡系統在實際的應用過程中，不僅僅具有更快的學習速度，同樣也表現出更為快速的收斂能力。充分證明了改進型小波神經網絡在變壓器故障診斷工作中應用的有效性，該算法的優勢進一步得到了驗證，在變壓器故障診斷操作中取得了很好的診斷效果。

［1］朱敏，王富榮.引用神經網絡的變壓器故障專家系統［J］.計算機與現代化，2004，31(4):31-32，35.

［2］龍銀芳，趙知勁，沈雷.基于神經網絡和粒子群算法的 MCCDMA 多用戶檢測［J］.電子器件，2009，5(10):985-988.

［3］Zhenyuan W，Nien-chung W，Tzong-Yih G，et al.Artificial Intelligence in Power Equipment Fault Diagnosis［C］//IEEE PES Winter Meeting.2000，1:128-133.

［4］許暉，焦留芳，韓西寧.基于兩級神經網絡的傳感器在線故障診斷技術研究［J］.傳感技術學報，2008，10:1794-1797.

［5］李目，何怡剛，周少武，等.一種差分進化算法優化小波神經網絡及其在弱信號檢測中的應用［J］.計算機應用與軟件，2010，3:29-31，39.

［6］Szu H H.Shubha Kadambe Neural Network Adaptive Wavelets for Sianal Representation an Classification［J］Optical Engineering，1992，31(9):1907-1919.

［7］85-92DE Jong K A.An Analysis of the Behavior of a Class of Genetic Adaptive System［D］.Ph.D Dissertation，University of Michigan，No.76-9381，1975.

［8］汪光陽，周義蓮.煤氣鼓風機故障診斷的神經網絡模型研究與實現［J］.計算機應用與軟件，2011，2:90-92.

［9］Uardado J L，Naredo J L，Moreno P，et al.A Comparative Study of Neural Network Efficiency in Power Transformers Diagnosis Using Dissolved Gas Analysis［J］.IEEE Trans on Power Delivery，2001，16(4):643-647.