馬氏體相變研究的最新進展(六)

劉宗昌，計云萍

(內蒙古科技大學材料與冶金學院，內蒙古包頭 014010)

5 馬氏體相變的切變機制及其誤區

1924年Bain提出了馬氏體相變機制的第一個模型，為壓縮應變模型。1930年提出第1個切變模型，在以后的40余年中提出了一系列切變模型，由于每個模型均難以與實際符合，不斷修改或“完善”，到70年代共提出了8個晶體學切變模型。但最終所有的切變模型均與實際不符。馬氏體相變的形核長大、馬氏體形貌、纏結位錯、精細孿晶、微細層錯、位向關系、表面浮凸等試驗現象均不能用切變機制作出明晰而合理的解釋。晶格切變耗能太大，相變驅動力無力克服切變應變能。馬氏體相變的切變學說無論實踐檢驗還是理論檢驗都是不合格的，因此馬氏體相變的切變“理論”尚不能稱為理論，而是不完整、不成熟的學說。

造成切變學說誤區的原因之一是沒有采用系統科學的方法進行研究。在20世紀，材料科學家首先研究了珠光體轉變機理，緊接著就進行了馬氏體相變機理的研究，因為珠光體組織和馬氏體組織發現最早。學者們分別孤立地進行了共析分解機理和馬氏體切變機理的研究。而貝氏體組織的發現較晚(約晚60年)，20世紀50年代，貝氏體相變機制開拓者則借用了馬氏體的切變機制來解釋貝氏體的成因。20世紀70年代，擴散學派利用共析分解理論解釋貝氏體相變。他們都忽視了貝氏體相變的過渡性，都沒有把過冷奧氏體轉變作為一個整合系統來研究，忽略了共析分解、貝氏體相變、馬氏體相變三者的相關性、過渡性、交叉性，孤立地進行了馬氏體相變切變機制的研究。

20世紀前半葉，材料研究設備儀器落后，而SEM、TEM、HRTEM、STM等均是20世紀后半葉才投入應用的，因此對馬氏體相變和馬氏體的物理本質缺乏深入細致的試驗觀察，所提出的切變機制缺乏充分的試驗依據，造成理論上的重重誤區。

5.1 馬氏體相變切變機制的研究歷程及評價

過冷奧氏體的轉變是一個整合系統，應當將共析分解、貝氏體相變、馬氏體轉變作為一個整體，運用系統科學的方法進行研究。但歷史上，貝氏體組織的發現晚于馬氏體組織近60年，也即人類對馬氏體相變的研究早于貝氏體相變約半個世紀，因此，馬氏體相變的研究一直處于“孤立”的狀態，缺乏與中溫轉變的聯系，不能從貝氏體相變研究中獲得啟發。相反，20世紀50年代提出的貝氏體相變機制，卻借用了馬氏體相變的尚不成熟的研究結果，指出貝氏體相變具有馬氏體相變那樣的切變機制。

70年代，美國學者Aaronson從能量上否定了切變學說，指出貝氏體就是共析分解的產物，認為貝氏體相變具有共析分解那樣的擴散機制［30］。從而導致了貝氏體相變形成兩個學派，即切變學派和擴散學派，并且兩派進行了近40年的學術論爭。就這樣，馬氏體相變機制的研究一直沒有納入過冷奧氏體整合系統，而“孤軍奮戰”到20世紀末。使學術界誤認為切變機制是成熟的理論，至今，切變學說仍然被一些學者“奉為至寶”。

劉宗昌等人運用系統科學的方法，吸收了國內外學者正確的研究成果，同時指出了兩派的錯誤觀點，指出貝氏體相變既非切變過程，也非共析分解;并提出了貝氏體相變新機制，實現了貝氏體相變理論的整合［33］。貝氏體相變研究的新進展為馬氏體相變的研究提供了新思路，促進了馬氏體相變機制的研究。

馬氏體相變機制與中溫區的貝氏體相變存在密切的聯系，它是過冷奧氏體從中溫區到低溫區，相變過程逐漸演化的結果。研究馬氏體相變機制不能割裂與貝氏體相變的聯系。

1878年，索拜Sorby首先用金相顯微鏡觀察到淬火高碳鋼中的硬相，即高碳馬氏體組織。

1895年法國學者Osmond將鋼中的這種硬相命名為馬氏體(Martensite)。

1924年，美國學者Edgar Bain提出馬氏體相變具有表面浮凸現象。并且提出了馬氏體相變的應變模型，稱為貝茵模型。

1926～1927年，W.L.Fink和 Γ.Β.庫爾久莫夫等人各自分別用X-射線技術測得鋼中馬氏體為體心正方結構，并且第一次指出馬氏體是碳在α-Fe中的過飽和固溶體。此發現在當時具有理論意義，此定義一直延續到20世紀末才有人提出修改意見。人們發現不僅鋼中存在馬氏體相變，而且在有色金屬及合金，陶瓷材料中都可發生馬氏體相變。故該定義過時。

1929年，周志宏等首先將電解鐵淬入水銀，獲得馬氏體組織。此舉證明，馬氏體也可以是體心立方結構，不為碳所過飽和。

1930年，Γ.Β.庫爾久莫夫和 G.薩克斯(Sacks)首先測得1.4%C鋼中馬氏體與母相奧氏體保持一定的晶體學位向關系，即K-S關系［34］。據此設計了K-S切變模型，從此開始了馬氏體相變切變機制、相變晶體學的研究。

1933年，R.E.邁爾(Mehl)測得中、高碳鋼中馬氏體在奧氏體的{225}γ晶面上形成，稱其為慣習面［35］。

1934年，西山測得Fe-Ni合金馬氏體相變時存在西山關系，并且設計了西山模型。它具有K-S模型同類的缺點。

1 949年，Greniger和Troiano測定了Fe-22%Ni-0.8%C合金中的馬氏體位向，發現了G-T關系［36］。并提出馬氏體相變是無擴散的切變過程。該模型力圖解釋位錯和孿晶的存在和表面浮凸的形成。

1951年，J.W.Christian首先提出了馬氏體相變的層錯形核模型［37］。

1953年，Frank首先提出Fe-C{225}γ馬氏體與母相間的位錯界面模型。促成了K-D位錯胞核胚模型的提出。但K-D位錯胞馬氏體核胚模型至今沒有得到試驗證實。母相和馬氏體中均不可能存在如此高的位錯密度，理論上與實際不符。

1953～1954年，由 M.S.Wechsler等(W-L-R)和J.S.Bowles等(B-M)分別獨立地提出兩個馬氏體相變的表象學假說，其一稱為“W-L-R理論”;另一個稱為“B-M 理論”［38－39］。兩者基本上等價，即指兩者的出發點和推理過程相近。學術界稱其為出色的“表象學理論”，現在從試驗和理論上分析，這兩個學說的物理模型是錯誤的，因此其計算結果與實際不符是必然的，雖然個別合金中計算結果與實際符合，但計算機算出的結果是個案，不可信。

馬氏體相變表象學說將貝茵應變B，形狀應變F，簡單切變S和剛性轉動R，用一個矩陣式描述:即F=RBS。此計算式的物理模型不正確，其中:

1)貝茵應變B太大，達21%，這與實際不符;

2)形狀應變F，用浮凸值表示，浮凸是相變比體積變化所致，是一級相變的必然結果，并非切變過程。

3)簡單切變S，不能獲得真正的馬氏體晶格參數，并且耗能太大。

4)剛性轉動R是虛擬的，實際上不存在。

物理模型的不當，必導致計算結果與實際不符，雖然在Au-Cd等合金中得到證實，但僅是個案，不具普適性。對于低碳鋼、中碳鋼、高碳鋼馬氏體的計算結果與實際均不符。針對Fe基馬氏體，在20世紀70年代提出了非均勻切變模型，即所謂“近代唯象理論”。該假說較原始表象學說作了更多的假設，處理更復雜，但是在定量計算上仍然無能為力［37］。

1964年，Bogers-Burgers雙切變模型被提出。

60年代末，70年代初，先后提出馬氏體相變的協作形變“理論”和范性協作模型，以及多次切變模型。到20世紀末就馬氏體相變機制已經提出8種切變模型，但均不夠成熟。

總之，19世紀末到20世紀前葉，學者們分別孤立地進行了珠光體轉變、馬氏體相變和貝氏體相變的研究，雖然取得了一定的成果;但不足之處是沒有把過冷奧氏體作為一個整合系統來研究，理論研究缺乏系統性，整體性，忽略了共析分解、貝氏體相變、馬氏體相變三者之間的內在聯系。在沒有應用先進設備搞清其物理本質的情況下，過早地確定其轉變機制，因而出現認識上的偏差和錯誤在所難免。

直到20世紀末，馬氏體相變切變機制的研究也沒有形成完整而成熟的理論體系，假說多，模型多，與實際相差甚遠。

5.2 馬氏體相變晶體學的經典模型

相變晶體學是相變機制的核心內容，如果說相變熱力學、動力學的研究是外圍戰，那么，晶體學的研究則是攻堅戰。一個世紀以來，馬氏體相變晶體學研究進行了大量理論研究工作，提出許多模型或假說。

20世紀對馬氏體相變晶體學的研究經歷了三個階段:

第一階段，1924年Bain提出了應變模型。該模型不能說明慣習面，而且應變太大，不能說明馬氏體的亞結構等，故為人們所擯棄。

第二階段，從1930年開始，提出了一系列晶格切變模型，如K-S模型、西山模型、G-T模型、B-B雙切變模型、藤田模型等。這些模型均為針對某一具體發現的事例，設計一種切變模型，以說明相變時原子的具體移動方式，說明位向關系、慣習面等。但是，這些切變模型均不能與實際完好地吻合。

第三階段，50年代初，提出了馬氏體相變晶體學唯象學說。晶體學唯象學說只推測相變過程的表象，而不能描述原子的遷動過程。它吸收了貝茵應變模型和切變模型的成分，從“不變平面應變”這一個基本觀點出發，設計了一套可以定量計算的應變模型。力圖說明母相、新相的點陣結構、位向關系、慣習面(指數)、外形變化、亞結構之間的關系，但多與實際不符。

上述三個階段中，形成了許多個模型或假說，科學技術哲學告訴我們，假說只有不斷地被證實，才能上升為理論。因此切變機制尚不是成熟的理論。以下僅介紹幾種經典的切變模型。

5.2.1 K-S切變模型和西山模型

5.2.1.1 K-S 切變模型

20世紀30年代初，庫氏和Sachs確定了1.4%C鋼中奧氏體與馬氏體之間的位向關系為:

{111}A//{011}M＜110＞A//＜111＞M此稱為K-S關系。據此設計了材料學界眾所周知的K-S晶格切變模型。

根據K-S關系，新相和舊相晶體的密排原子面相互平行，認為相變時，母相的{111}γ面將轉變為新相的{011}α面。因此，首先需要弄清{111}γ和{011}α面的原子排列情況和堆垛次序。見圖63，底面為密排面{111}γ。堆垛次序為ABCABCAB……，●表示底層原子A，⊕表示中間層(第二層)原子B，○表示頂層(第三層)原子C。

圖64(a)是1.4%的Fe-C馬氏體的原子排列情況和堆垛次序，為體心正方結構(bct)，底面為{011}α。圖64(b)圖是體心立方結構的α-Fe的原子排列情況和堆垛次序，底面也為{011}α。

切變分三步進行:

圖63 {111}γ面原子堆垛Fig.63 Atomic stacking of{111}γ

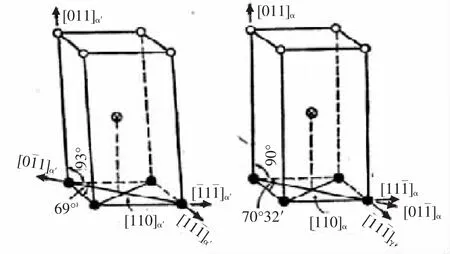
圖64 (a)體心正方馬氏體和(b)體心立方α-Fe原子堆垛Fig.64 Atomic stacking of(a)body-centered tetragonal Martensite and(b)body-centered cubic α-Fe

1)第一切變:見圖65，底面為{111}γ菱形，菱形角為60°。切變在{111}γ面上，沿著［11］γ方向進行，底層原子不動，第二層?原子沿［211］γ方向移動0．057nm，○層原子移動0．114nm，切變角為19°28';含碳 1．4% 的 Fe-C 馬氏體(c/a=1．06，下同)，切變角則為 15°15'。

2)第二切變:在{211}α面上，沿著［111］α方向進行一次小的切變，使60°角變成69°。如果不含碳，則使 60°角變成 70°32'，如圖 66 所示。

3)第3步，晶格線性調整，為使其符合實際的馬氏體晶格的面間距等參數，轉變為bccM(0%C)，進行晶格參數調整，晶格參數調整量列于表3中。

各切變參數依下列各式計算:

許多書中將上述過程集中描繪在一個圖中，即將原子的遷移情況投影在底面菱形上，來表示切變全過程，圖67為K-S切變模型的平面投影［6］。圖67(a)表示{111}γ上原子的排列情況，圖67(b)表示第一切變后的情況，圖67(c)表示第二切變后的情況，圖67(d)表示經調整成c/a=1.06的體心正方結構，圖67(e)表示經過調整成體心立方 α-Fe的{011}α面上的原子排列情況。

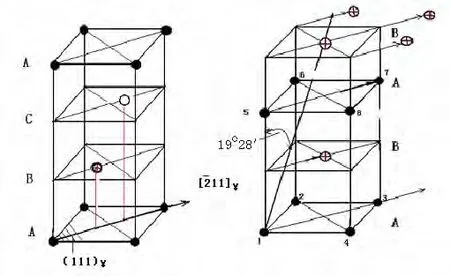
圖65 K-S第一切變Fig.65 The first shear of K-S

圖66 K-S第二切變Fig.66 The second shear of K-S

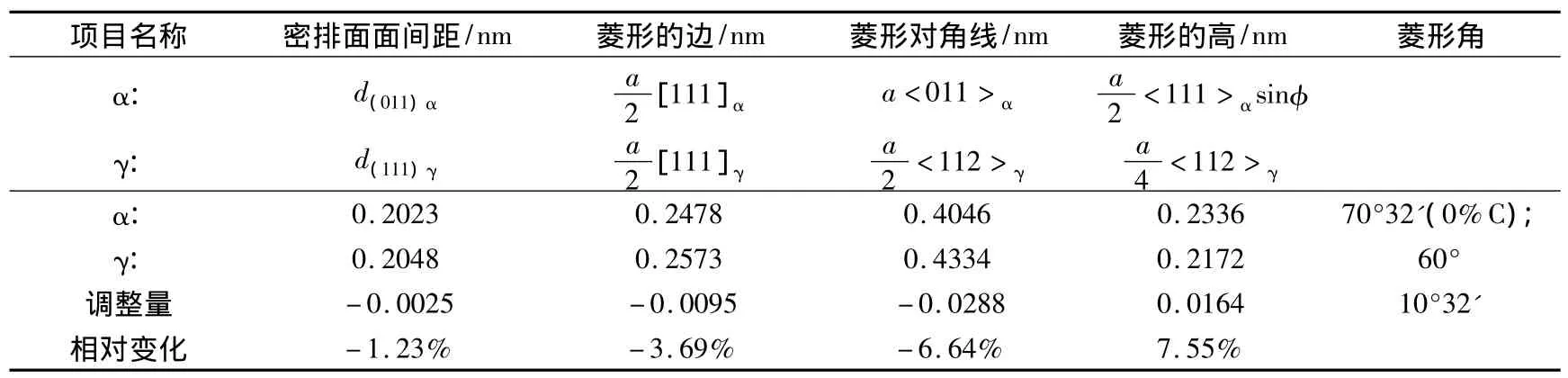
表1 γfcc→αbcc時主要晶格參數變化Table 1 The changes of main parameter of crystal lattice at γfcc→αbcc

5.2.1.2 西山切變模型

1934年，西山善次研究了Fe-Ni(34% ～37%Ni)合金的馬氏體相變，發現西山關系。并且提出一個切變模型，被稱為西山模型。此模型的第一次切變與K-S模型相同，也是在{111}γ晶面上，沿著［211］γ方向切變19°28'。但隨后不進行K-S模型的第二次切變，而是直接進行晶格參數調整，如使［211］γ軸收縮7.5%，［111］γ軸收縮1.9%，［110］γ軸膨脹13.3%，再使底面內角由60°調整到70°32'。經過這些調整，使其與實際的馬氏體晶格相符。西山關系與 K-S 關系相差 5°16'［6］。

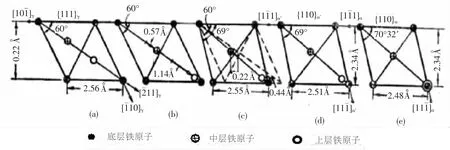
圖67 K-S切變模型的平面投影Fig.67 The plane projection of K-S shear model

5.2.1.3 K-S 模型和西山模型的誤區

兩個模型通過晶格切變，力圖得到了體心立方結構的馬氏體，但問題較多:

1)慣習面不符合。按此模型，慣習面應為{111}γ，而實際上 Fe-C合金馬氏體的慣習面有{557}γ、{225}γ、{259}γ;具有西山關系的 Fe-Ni(34% ～37%Ni)合金，其慣習面是{259}γ，而非{111}γ。

2)不能解釋馬氏體中孿晶、位錯、層錯等亞結構的形成，也不能解釋浮凸現象。

3)不符合省能原則。該模型的第一、第二兩次切變，是單晶體的晶格切變(當時還沒有發現位錯、孿晶缺陷)這種晶格切變消耗的切變能太大，相變驅動力不足以完成切變過程［40］。

4)按照K-S模型和西山模型，第一切變后，并沒有改變晶格類型，如切變前的堆垛方式是ABCABCABC…….，切變后變為ABABAB………，相當于抽出了C層。而A層、B層上的原子排列仍然與母相fcc上的A層、B層相同。即按照塑性變形理論，單純的切應變是不能改變晶格類型的。

5)按照K-S模型，第一、第二兩次切變后并沒有得到實際的馬氏體晶格，還需要調整晶格參數。西山模型的切變與K-S模型的第一切變相同，但不進行第二切變，然后進行晶格參數調整。晶格參數的調整需要原子再位移，怎么位移?位移就要再耗能。這些模型均沒有考慮。

6)設想若省略第一切變、第二切變，直接進行晶格參數調整，將所有晶格參數均調整為馬氏體的晶格參數，就實現了晶格重構，變成了馬氏體。何必要切變呢?而且切變耗能太大，熱力學上不可能實現。

即使按照切變學說發生了晶格切變過程，切變也沒有得到符合實際的真正的馬氏體晶格參數。按照金屬學原理，塑性變形不能改變晶格類型，因此這些模型均指出還需要晶格參數調整。奧氏體轉變為馬氏體本來就是晶格重構的過程，就是晶格參數調整的過程。因此切變是多余的動作，是臆造出來的。

面心立方的母相轉變為體心立方的馬氏體相，就是晶格重構的過程，即晶格參數調整的過程。這種調整是母相原子向新相熱激活遷移過程，是新舊相自由焓差作用下的自發過程。切變徒勞無功，反而消耗了巨大的切變能。因此切變模型不可取。

5.2.2 馬氏體相變的G-T模型

G-T模型也是一個具有代表性的經典模型。在1 949年A.B.Greninger和A.R.Troiano測得了Fe-22Ni-0.8C合金單相奧氏體轉變為馬氏體，慣習面為{259}γ，其位向關系接近K-S關系，稱為G-T關系，實際上是偏離K-S關系1°～2°，即:

{110}α'//{111}γ差1°

＜111＞α'//＜110＞γ差2°

據此G-T關系，他們以均勻切變和非均勻切變合成的方式，提出了G-T模型。指出可以在主切變的基礎上沿著“馬氏體”一定的晶面進行第二次切變。沿著慣習面的第一次切變為主切變，是均勻切變，而第二次切變是非均勻切變。如圖68所示。

物體的應變分為均勻應變和非均勻應變兩類。均勻應變是指系統內每一個基本單元，如每個晶胞發生的應變量等于宏觀應變量。如熱膨脹即是常見的均勻應變。從晶格的角度講，均勻應變總是晶格類型的改變或晶格參數的變化。非均勻應變就是系統內各部分應變量不同，如金屬的塑性變形在微觀上是不均勻的。

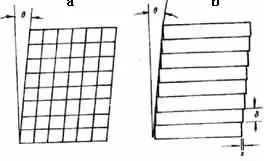
圖6 8(a)均勻切變和(b)非均勻切變Fig.68 (a)homogeneous shear and(b)non homogeneous shear

從圖68可見，為了獲得宏觀切變角θ，可以采用均勻切變的方式，也可以采用非均勻切變的方式。非均勻切變可以通過δ和s的調整，采用滑移的方式或孿生的方式均可以達到目的。但δ值要比晶格常數大得多時，非均勻應變不改變晶格類型及參數。

圖69是G-T模型的示意圖，其中圖69(a)表示以慣習面(中脊面)為基準的均勻切變，即主切變。圖69(b)表示二次切變(滑移)的發生面，以及切變后外形的變化。二次切變是在經過主切變的“馬氏體”中沿著{211}α晶面，在［111］α方向反復地進行滑移。

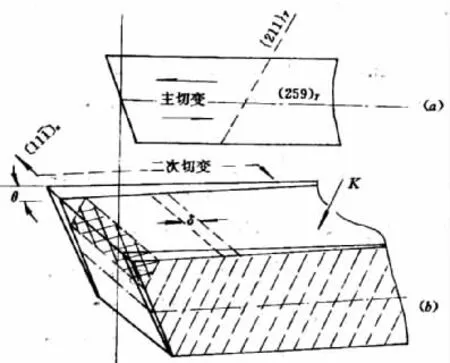
圖69 G-T模型示意圖Fig.69 Sketch map of G-T model

按照G-T模型，當非均勻切變區間距(δ)小于一定數值時，配以適當的切變量(s)，二次切變發生宏觀為θ的切變。如果從圖69的K方向看去，二次切變的情形如圖70所示，θ為12°～13°，δ有十幾個原子層厚。

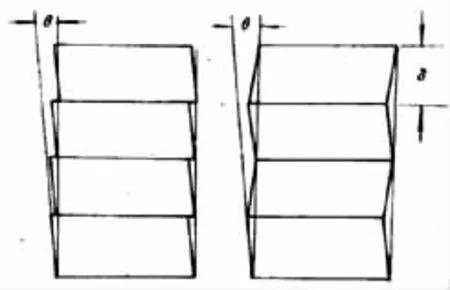
(a)滑移;(b)孿生圖70 二次切變(a)sliding;(b)hemitropism Fig.70 The secondary shear

完成G-T模型兩次切變后，并沒有完全達到實際馬氏體晶體的要求，為了與實際的馬氏體晶體相符，尚需作晶格參數調整。

G-T模型存在的問題是:

1)與慣習面不符，如該合金的慣習面實際是(225)γ，而非(259)γ。與小于1.4%C 的鋼中馬氏體的慣習面也不相符。

2)雖然預示馬氏體中出現位錯和孿晶，但是馬氏體中的孿晶是相變孿晶，不是形變孿晶;是相變位錯，不是形變位錯。因此該模型不能解釋馬氏體中復雜的纏結位錯、精細孿晶、層錯形成的實際成因。也不能解釋鋼中馬氏體的正方度。

3)兩次切變沒有得到真正的馬氏體晶格，切變后仍然需要晶格參數調整，需要原子的再移動。

4)切變能量消耗太大，缺乏熱力學可能性。

G-T模型的切應變動作是晶體在外力作用下的滑移和孿生，金屬塑性變形不能改變晶格類型，因此將塑性變形的滑移和孿生應用于相變過程是不妥當的，馬氏體中的位錯和孿晶是相變過程中形成的，是相變位錯和相變孿晶，不是形變造成的，二者不能混淆。

G-T模型完成兩次切變消耗了巨大的切變能。遺憾的是切變后并沒有得到實際的馬氏體晶格，仍需進行晶格參數調整，才能與實際的馬氏體晶格參數相同。這實際上是需原子再移動，再耗能，在已經消耗切變能量基礎上還需要追加晶格參數調整的能耗。

總之，G-T模型沿襲了K-S、西山模型同樣的錯誤，因此也是不可取的。

值得注意的是:Ti-5Mo合金中，成分與結構相同的母相形成的α馬氏體，為六方結構，慣習面接近{344}β，但是沒有亞結構，無亞結構的馬氏體雖然少見，但也是馬氏體相變。沒有位錯，也沒有孿晶，還需要按G-T模型進行切變嗎?還需要滑移或孿生嗎?更應當注意的是:至今研究發現，不僅在有色金屬的馬氏體中存在層錯亞結構，在低碳鋼、高碳鋼、鐵基合金馬氏體中普遍存在層錯亞結構，而層錯馬氏體的形成不能用位錯滑移或孿生等切變機制解釋。可見切變模型是與實際馬氏體相變無關的學說，是錯誤的。