基于土拱效應(yīng)的抗滑樁間距計(jì)算方法綜述

馬飛，郭長春

（1重慶市地質(zhì)災(zāi)害防治中心，重慶 401311；2重慶建工第三建設(shè)有限責(zé)任公司，重慶 400011）

0 引言

抗滑樁通常用于穩(wěn)定邊坡和治理滑坡[1-2]，是將樁插入滑動面（帶）以下的穩(wěn)定地層中，利用穩(wěn)定地層巖土的錨固作用以平衡滑坡推力，穩(wěn)定滑坡的一種結(jié)構(gòu)物[3]。由于坡體的橫向位移大于抗滑樁的橫向位移，使樁迎坡面一側(cè)土體相互擠壓，土體抗剪能力得到發(fā)揮從而形成了土拱效應(yīng)，如圖1所示。抗滑樁的設(shè)計(jì)理念是采用非連續(xù)結(jié)構(gòu)，利用土體自身強(qiáng)度形成的拱效應(yīng)將樁間土體的下滑推力傳遞到樁身來達(dá)到支擋的目的[4]。合適的抗滑樁間距是產(chǎn)生土拱效應(yīng)的前提，而只有產(chǎn)生土拱，抗滑效果才比較明顯[5]。而實(shí)際樁間距計(jì)算中，通常通過單樁承載力或是經(jīng)驗(yàn)進(jìn)行估計(jì)，不僅結(jié)果偏于保守，而且造成了不必要的浪費(fèi)，因此合理樁間距的確定具有重要的實(shí)踐意義。

圖1 樁間土拱效應(yīng)示意簡圖

1 基于土拱效應(yīng)的計(jì)算方法

由于對土拱作用機(jī)理、破壞機(jī)制和強(qiáng)度條件等認(rèn)識的不同，對土拱的計(jì)算方法也是各不相同，總體來說分為三種類型：（1）通過土拱靜力平衡條件得到最大樁間距的計(jì)算方法；（2）運(yùn)用大小主應(yīng)力理論建立的樁間距的計(jì)算方法；（3）以土拱強(qiáng)度為約束條件建立的計(jì)算方法。

1.1 靜力平衡法

靜力平衡法是由土拱受力保持靜力平衡，得到靜力平衡式，進(jìn)而推算出樁間距的方法，主要以樁側(cè)摩阻力與滑坡推力間的靜力平衡條件進(jìn)行控制。王世川[6]認(rèn)為應(yīng)在樁間距上限值解法的基礎(chǔ)上考慮土拱效應(yīng)的影響，同時(shí)也應(yīng)注意樁斷面間土體摩阻力和粘著力的阻滑作用。文獻(xiàn)6以土拱效應(yīng)為基本條件，樁間滑坡推力小于土體與樁側(cè)間的摩阻力，得到下限解的計(jì)算式：

式中，R為微元體上的平均壓應(yīng)力，S為抗滑樁的中心距（m）；ψ為土拱影響系數(shù)；δ為樁與樁周巖土間的摩擦角（°）；D為樁的長邊長度（m）；h為滑體厚度（m）；λ為微元體水平應(yīng)力與垂直應(yīng)力之比。其余為土的物理力學(xué)參數(shù)。

過大的滑坡推力與土拱內(nèi)部較低的土顆粒抗剪強(qiáng)度耦合作用會造成土拱破壞[7]。王成華假設(shè)樁間全部滑坡推力通過樁側(cè)摩阻力承擔(dān)，得到最大樁間凈距計(jì)算公式：

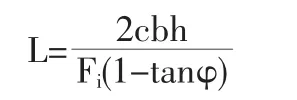
式中，c為沿滑動面滑動土體的內(nèi)聚力（kPa）；b為抗滑樁側(cè)滑動面以上寬（m）；h為抗滑樁側(cè)滑動面以上高（m）；Fi為單寬滑坡推力（kN/m）；φ為土拱土體的內(nèi)摩擦角（°）。

馮君在王成華法的基礎(chǔ)上認(rèn)為滑坡推力不僅通過樁側(cè)摩阻力承擔(dān)，而且土拱自身的剩余抗滑力與拱前巖土體也同時(shí)參與阻滑，通過引入隧道工程的普氏系數(shù)得到最大樁間凈距的計(jì)算公式[8]：

式中，F(xiàn)i為豎向均布荷載（kN/m）；fkp為普氏巖土體堅(jiān)固性系數(shù)；δ為樁與樁周巖土間的摩擦角（°）；b為土拱沿滑動方向的厚度（m）；c為土體粘聚力（kPa）；h為滑體厚度（m）。

以上理論均從土拱的靜力平衡條件著手，考慮了樁側(cè)摩阻力影響，但在滑坡推力的承擔(dān)問題上相異。單一以樁側(cè)摩阻力承擔(dān)滑坡推力會使計(jì)算偏于保守，而樁前土體的阻滑作用并不明顯，提供抗滑力顯然不太合理，所以明確阻滑條件是應(yīng)該值得注意的問題。

1.2 大小主應(yīng)力法

顆粒體系受縱向力作用，會發(fā)生應(yīng)力偏轉(zhuǎn)而傾于橫向分布，從而形成以主應(yīng)力跡線為拱軸線、約束處為拱腳的拱[9]。而在相鄰護(hù)壁樁之間會形成大主應(yīng)力拱[10]，且應(yīng)力值為常量[11]。大主應(yīng)力拱支撐其后方土體，從而使土體保持穩(wěn)定。胡敏云通過假定圓弧曲線為拱軸線，以大小主應(yīng)力理論建立了樁間凈距的計(jì)算公式[12]：

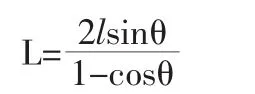
式中，l為拱高（m）；θ為大主應(yīng)力拱切線方向與水平線的夾角（°）。

上述公式形式簡單，并且可通過l值考慮樁間土剝落區(qū)域的合理范圍，但把樁間土拱假定成圓弧曲線顯得不太合理。李邵軍通過有限元分析得到樁后存在四種土拱形態(tài)[13]，所以只通過大主應(yīng)力拱一種形式進(jìn)行分析并不太合理。賈海莉認(rèn)為土拱效應(yīng)中存在著大主應(yīng)力拱和小主應(yīng)力拱的共同作用，而抗滑樁作用的土體平面應(yīng)分為穩(wěn)定區(qū)、土拱區(qū)和自由區(qū)[14]。穩(wěn)定區(qū)和土拱區(qū)的土體下滑力由大主應(yīng)力拱承擔(dān)，自由區(qū)土體下滑力主要由小主應(yīng)力拱承擔(dān)。考慮到穩(wěn)定區(qū)和自由區(qū)土體穩(wěn)定的重要性，通過大主應(yīng)力拱的作用建立了樁間凈距的計(jì)算式：

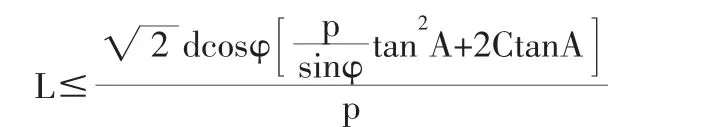
式中，p為土拱后作用的均布水平荷載（kN/m）；C為土體的粘聚力（kPa）；φ為土體的內(nèi)摩擦角（°）；A=π/4+φ/2 ；d為土拱寬度（m）。

賈海莉法將樁作用土體平面分區(qū)，分清了阻滑主次，在樁間距的計(jì)算中突出了重點(diǎn)。但是在計(jì)算中忽略了小主應(yīng)力拱的作用，結(jié)果往往偏大，如果運(yùn)用上述公式布置樁位，難以保證自由區(qū)土體的穩(wěn)定性，所以在必要時(shí)應(yīng)同時(shí)考慮大小主應(yīng)力拱的作用。

1.3 強(qiáng)度條件法

以土拱強(qiáng)度條件為基礎(chǔ)確定樁間距的方法，統(tǒng)稱為強(qiáng)度條件法。僅通過強(qiáng)度條件難以得到可靠樁間距，例如常保平法[15]計(jì)算結(jié)果存在一定的偏差。因此強(qiáng)度條件必須和靜力平衡條件同時(shí)考慮，才能較為準(zhǔn)確的計(jì)算合理樁間距的大小。

1.3.1 根據(jù)樁間水平土拱強(qiáng)度條件建立的樁間距計(jì)算方法周德培認(rèn)為樁間土拱的形式為二腳拱，提出矩形截面樁間土拱應(yīng)滿足三個(gè)強(qiáng)度條件：（1）樁側(cè)摩阻力之和不小于樁間作用于土拱上的壓力；（2）跨中截面處前緣點(diǎn)應(yīng)該滿足莫爾-庫侖強(qiáng)度準(zhǔn)則；（3）樁體后側(cè)的三角形受壓區(qū)應(yīng)能滿足強(qiáng)度條件[16]。綜合上述條件建立最大樁間凈距的計(jì)算公式：

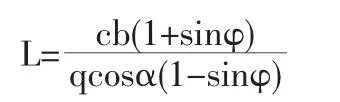
式中，q為作用于單位高度土拱上的樁后坡體線分布壓力（kN/m）；c為樁間后側(cè)土體的粘聚力（kPa）； φ為樁間后側(cè)土體的內(nèi)摩擦角（°）；α為三角形受壓區(qū)斜邊與水平方向的夾角（°）；b為樁徑（m）。

周培德法確定的樁間距滿足了土拱的強(qiáng)度條件，但卻假定了土拱沿樁長均勻分布，而在實(shí)踐中土拱是由樁頂向下逐漸減小的，這無疑夸大了土拱效應(yīng)，使得樁間距計(jì)算結(jié)果偏大，所以必須除以適當(dāng)?shù)陌踩禂?shù)[17]來作為實(shí)際樁間距。趙明華將合理拱軸線作為土拱軸線，因?yàn)榭够瑯对谧杌^程中是被動受力的，所以假定拱軸線起點(diǎn)切向角β=π/4+φ/2，結(jié)合樁側(cè)摩阻力之和應(yīng)大于土拱所受壓力與跨中截面處土體應(yīng)滿足的強(qiáng)度條件，得到計(jì)算公式[18]：

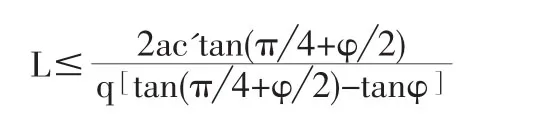
式中，L為樁間凈距（m）；q為土拱后作用的均布水平荷載（kN/m）；a為抗滑樁側(cè)面寬度（m）；φ'、c'分別為滑坡體與樁體間的內(nèi)摩擦角（°）和粘聚力（kPa）；φ為室內(nèi)試驗(yàn)給出的接觸面上的內(nèi)摩擦角（°）。

由于土體參數(shù)具有變異性，且對模型本身進(jìn)行了簡化假定，樁距計(jì)算必須根據(jù)工程實(shí)際進(jìn)行綜合考慮。而在拱角問題的處理上，目前意見仍不統(tǒng)一，需要今后深入研究。劉靜認(rèn)為土拱存在三種破壞形式：（1）土拱水平方向的平衡失效；（2）土拱豎直方向的平衡失效；（3）土拱拱腳處材料的強(qiáng)度失效[19]。結(jié)合這三種破壞形式獲得相應(yīng)的平衡控制條件，得到以下公式：

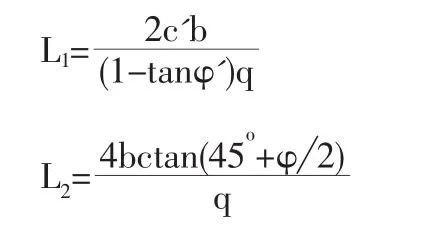
合理樁間距為：

S=Lmax+b

式中，L1為保證拱腳最不利破壞面土體抗剪強(qiáng)度的合理樁間凈距（m）；L2為保證土拱水平向和豎向平衡的合理樁間凈距（m）；φ為土體的內(nèi)摩擦角（°）；φ'為土體與樁體間的內(nèi)摩擦角（°）； c'為土體與樁體間的粘聚力（kPa）；b為樁側(cè)寬（m）；q為土拱后作用的均布水平荷載（kN/m）；c為土體的粘聚力（kPa）。

劉靜法對土拱拱腳給予了較大的重視，分別從水平和豎直方向闡明了其對于土拱強(qiáng)度的重要性，但其雖然綜合考慮了靜力平衡和土拱強(qiáng)度條件，但沒有考慮土拱頂部的強(qiáng)度條件，可能會使計(jì)算結(jié)果偏大。

1.3.2 根據(jù)斜拱效應(yīng)建立的樁間距計(jì)算方法

大部分計(jì)算方法都將抗滑樁后的土體假定為水平，但實(shí)際上滑坡的坡面往往是傾斜的。趙明華考慮了邊坡傾角對樁間距的影響，在假定土拱的軸線為拋物線的基礎(chǔ)上，根據(jù)水平面、豎直面內(nèi)的靜力平衡條件和強(qiáng)度條件，分別推導(dǎo)出兩個(gè)樁間凈距的計(jì)算公式[20]：

水平方向：

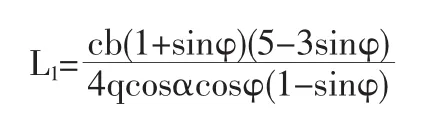
豎直方向：

式中，q為作用于單位高度土拱上的樁后坡體線分布壓力（kN/m）；α為坡面與水平面的夾角（°）；c為樁間后側(cè)土體的黏聚力（kPa）；φ為樁間后側(cè)土體的內(nèi)摩擦角（°）；b為樁正面寬度（m）。

從兩個(gè)樁間凈距的計(jì)算公式可知，存在一個(gè)臨界角度α0，當(dāng)坡面角α>α0時(shí)，豎直面內(nèi)的強(qiáng)度破壞為主要控制條件，這時(shí)取L2為抗滑樁的樁間凈距；當(dāng)α<α0時(shí)，水平面內(nèi)土拱截面的強(qiáng)度破壞為主要控制條件，這時(shí)則取L1為抗滑樁的樁間凈距[22]。在實(shí)際的抗滑樁間距設(shè)計(jì)中，應(yīng)分別計(jì)算兩個(gè)樁間距，取兩者中較小者為合理樁間距。在滑坡治理中由于抗滑樁的截面較大而常常設(shè)置混凝土或鋼筋混凝土護(hù)壁，護(hù)壁及護(hù)壁周圍漿液滲透的一定范圍得到改良或加固的土體—接觸帶，對滑坡均起提供抗力的作用[21]。而在土拱拱角的處理上，上述公式均沒有考慮接觸帶的作用。

1.3.3 根據(jù)三維有限元模型建立的樁間距計(jì)算方法

大多數(shù)樁間距計(jì)算都將模型簡化為平面模型，而樁間土拱效應(yīng)的幾何形態(tài)在豎向上是呈不規(guī)則分布的[13]，所以上述方法將土拱效應(yīng)在豎向上作了近似處理。張永興考慮了土體自重應(yīng)力的影響，通過有限元法建立了三維計(jì)算模型，并推導(dǎo)出最大樁間凈距計(jì)算公式[22]：

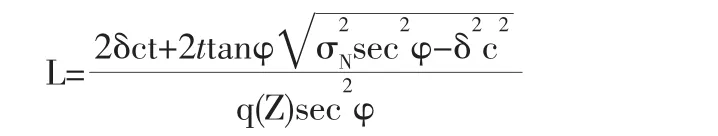
式中，δ為拱腳形狀系數(shù)，δ=1/cosθ，θ為拱腳處拱軸線的切線與水平線夾角（°）；c為滑體的凝聚力（kPa）；t為拱腳厚度（m）；φ為內(nèi)摩擦角（°）；σN為軸應(yīng)力（kN）；q（z）為土拱上作用單位面積的土壓力（kN/m2）；

通過有限元建立三維模型可以較為真實(shí)的模擬邊坡環(huán)境，并且可以考慮到土體自重應(yīng)力對土拱的影響。但是利用有限元進(jìn)行模擬的技術(shù)現(xiàn)在仍然不夠成熟，需要今后繼續(xù)完善。

2 幾種計(jì)算方法的比較

采用同樣的工程實(shí)例分別用上述計(jì)算方法計(jì)算，結(jié)果見表1。從表中可以看出，不同計(jì)算方法得到的樁間距差別很大。對于截面為2.0m×3.0m的抗滑樁，在同一滑坡推力的作用下方法2、4計(jì)算結(jié)果偏大，方法3、5計(jì)算結(jié)果偏小，其他方法計(jì)算的樁間凈距介于5～8m之間。

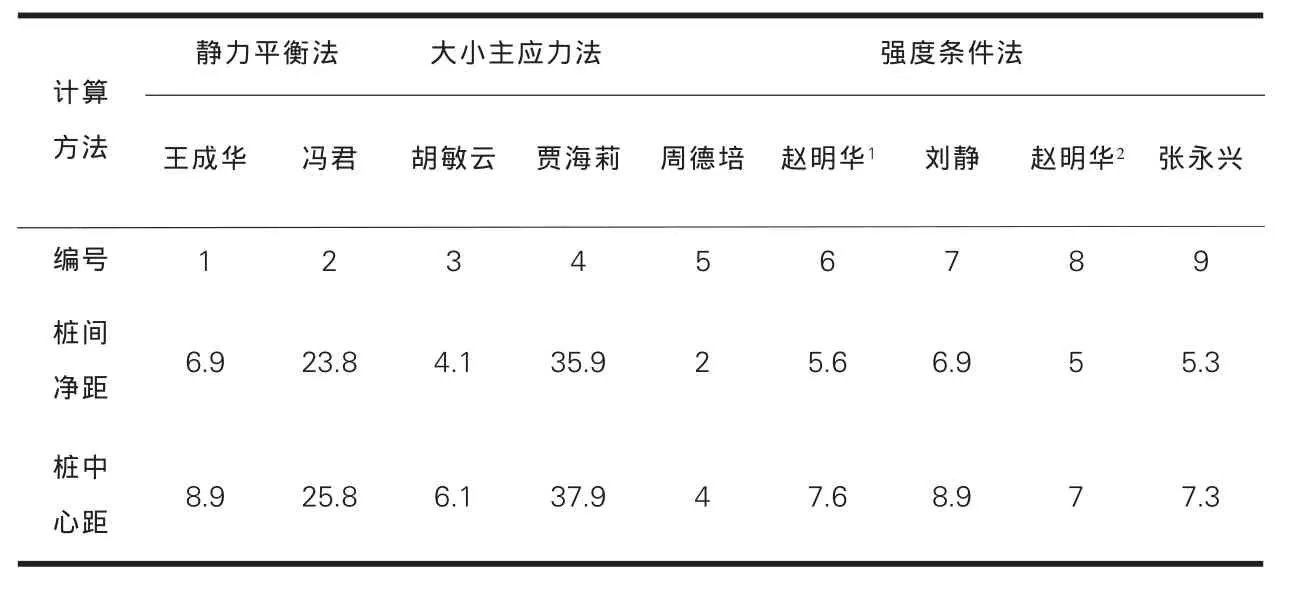
表1 各種算法計(jì)算結(jié)果對照表（單位：m）

3 存在的問題及建議

抗滑樁合理樁間距分析是一個(gè)受多種因素影響的問題，而樁間距的確定對抗滑樁阻滑性能的發(fā)揮、成本的控制起著重要作用，雖然已經(jīng)有很多通過土拱效應(yīng)計(jì)算樁間距的方法，但其中仍然存在一些問題需要進(jìn)一步探討：

（1）土拱的靜力平衡條件對樁間距的影響較大，但很多方法在滑坡推力的承擔(dān)問題上相異。若單一以樁側(cè)摩阻力承擔(dān)滑坡推力會使計(jì)算偏于保守，而樁前土體的阻滑作用并不明顯，提供抗滑力顯然不太合理，并且土拱自身的剩余抗滑力受土體參數(shù)的影響較大，所以明確阻滑條件是今后研究值得注意的問題。

（2）樁間土拱邊界是一個(gè)模糊的范圍。由于土拱的組成物和結(jié)構(gòu)與前后土體完全相同，所以樁間土拱與前后土體沒有明顯的界限，土拱沿滑動方向的厚度也不清楚。因此將樁間土體的支撐作用適當(dāng)分類，找出主要受力部分，從而得到樁間距的主要控制項(xiàng)是今后研究的重點(diǎn)。

（3）在樁間距的計(jì)算中，不同的土拱形式假定會對土拱受力情況產(chǎn)生影響，從而產(chǎn)生不同的計(jì)算結(jié)果，所以如何對土拱形式進(jìn)行準(zhǔn)確的描述有待今后繼續(xù)研究。

（4）土拱效應(yīng)具有時(shí)空特性，而大部分計(jì)算模型都將其簡化為平面問題，并忽略了地震、滲透等作用的影響，這很容易造成計(jì)算的失真，從而影響樁間距的確定，因此應(yīng)結(jié)合土拱效應(yīng)的時(shí)空特性來確定合理樁間距。

（5）在計(jì)算樁間距時(shí)，沒有考慮抗滑樁本身的力學(xué)性質(zhì)、截面形狀及其錨固深度等對土拱效應(yīng)的影響，會使計(jì)算失真，所以這一問題有待進(jìn)一步研究。

（6）如今大部分計(jì)算都集中在單排樁樁間距的確定上，但隨著抗滑樁的不斷發(fā)展，多排樁的大量運(yùn)用是一個(gè)不可避免的趨勢，因此有必要結(jié)合土拱效應(yīng)的作用對多排樁的樁間距問題進(jìn)行探討。

（7）利用數(shù)值模擬的方法可以從不同角度觀察土拱效應(yīng)對于樁間距的影響，并可以在成本較低的情況下，相對容易的獲取土拱各個(gè)性狀的參數(shù)。所以數(shù)值模擬法是今后土拱效應(yīng)研究發(fā)展的趨勢。

[1]殷躍平，康宏達(dá)，陳波.三峽工程移民遷建區(qū)災(zāi)害地質(zhì)體改造與利用研究[J].工程地質(zhì)學(xué)報(bào)，2000，8（1）:73-80.

[2]王成華，陳永波.世壽街滑坡發(fā)生機(jī)理與防治對策[J].工程地質(zhì)學(xué)報(bào)，2000，8（3）:277-280.

[3]鄭穎人，陳祖煜，王貢先，等.邊坡與滑坡工程治理[M].北京：人民交通出版社，2007:394-395.

[4]吳子樹，張利民，胡定.土拱的形成機(jī)制及存在條件的探討[J].成都科技大學(xué)學(xué)報(bào)，1995（2）:15-19.

[5]張建華，謝強(qiáng)，張照秀.抗滑樁結(jié)構(gòu)的土拱效應(yīng)及其數(shù)值模擬[J].巖石力學(xué)與工程學(xué)報(bào)，2004，23（4）:669-703.

[6]王士川，陳立新.抗滑樁間距的下限解[J].工業(yè)建筑，1997，27（10）:32-36.

[7]王成華，陳永波.抗滑樁間土拱力學(xué)特性與最大樁間距分析[J].山地學(xué)報(bào)，2001（6）：556-559.

[8]馮君，呂和林，土成華.普氏理論在確定抗滑樁間距中的應(yīng)用[J].中國鐵道科學(xué)，2003，24（6）:79-81.

[9]厚美瑛，陸坤權(quán).奇異的顆粒物質(zhì) [J].新材料產(chǎn)業(yè)，2001，（2）:26-28.

[10]胡敏云，夏永承，高渠清.無錨撐樁排式支護(hù)護(hù)壁樁側(cè)土壓力計(jì)算方法[J].巖石力學(xué)與工程學(xué)報(bào)，2000，19（4）:517-521.

[11]WILLIAMS K H.Arch in soil arching [J].Journal of Geotechnical Engineering，1989，115（3）:415-419.

[12]胡敏云.深基坑護(hù)壁樁間距確定方法探討[J].中國公路學(xué)報(bào)，2001，14（2）：27—29.

[13]李邵軍，陳靜，練操.邊坡樁-土相互作用的土拱力學(xué)模型與樁間距問題[J].巖土力學(xué)2010，31（5）:1352-1357.

[14]賈海莉，王成華.基于土拱效應(yīng)的抗滑樁與護(hù)壁樁的樁間距分析[J].工程地質(zhì)學(xué)報(bào)，2004，12（1）:98-103.

[15]常保平.抗滑樁的樁間土拱和臨界間距問題探討:滑坡文集（第十三集）[M].北京:中國鐵道出版社，1998.73-78.

[16]周德培，肖世國.邊坡工程中抗滑樁合理樁間距的探討[J].巖土工程學(xué)報(bào)，2004，26（1）:132-135.

[17]鐵道部第一勘測設(shè)計(jì)院.鐵路工程設(shè)計(jì)技術(shù)手冊:路基[M].北京:中國鐵道出版社，1995.

[18]趙明華，陳炳初，劉建華.考慮土拱效應(yīng)的抗滑樁合理樁間距分析[J].中南公路工程，2006，31（2）:1-4.

[19]劉靜，吳海濤，胡煥校.由樁后土拱形成的條件對抗滑樁間距的計(jì)算[J].山西建筑，2009，35（36）:1-2.

[20]趙明華，廖彬彬，劉思思.基于拱效應(yīng)的邊坡抗滑樁樁間距計(jì)算[J].巖土力學(xué)，2010，31（4）:1211-1216.

[21]雷用，趙尚毅，郝江南，等.支擋結(jié)構(gòu)設(shè)計(jì)與施工[M].北京:中國建筑工業(yè)出版社，2010:22-23.

[22]張永興.考慮自重應(yīng)力的懸臂式抗滑樁三維土拱效應(yīng)及合理間距研究[J].中國公路學(xué)報(bào)2009，（2）：18-25.