基于極點展開法無芯片電子標簽的識別與傳感

胡 偉，鄒傳云，胥 磊，蘇立冬

（西南科技大學 信息工程學院，四川 綿陽 621010）

射頻識別技術（RFID）[1]是20世紀80年代發展起來的一種新興自動識別技術，射頻識別技術是一項利用射頻信號通過空間耦合，實現無接觸信息傳遞并通過所傳遞的信息達到識別目的的技術。目前無芯片RFID標簽類的識別，大都采用頻率內的幅度，相位等之間的變化關系，來對標簽結構的識別。但存在許多的限制，觀測的方位，激勵的入射角度，入射波的極化角度等變化，頻率內的數據也會隨之發生變化[2-6]。為克服這些限制，C.Baum提出奇點展開法[7-9]，在復頻域內，散射場的信號可以由極點與相應的留數共同表征，信號的特性由極點與留數確定，極點與散射體結構有關，與其它外部因素無關。留數則與其它的外界因素有關，可以通過留數的變化感知外界的條件因素。文獻[10]設計分析一種開槽型的標簽結構，本文在此研究的基礎上，進一步地利用極點展開的方法與理論，應用極點與留數的特性關系，不僅可以對標簽結構的識別，還可感知標簽結構其它特征。

1 極點展開法與矩陣束算法的相關理論

1.1 極點展開法的理論

根據C.Baum提出的理論，電磁波激勵金屬導體時，瞬態響應后期可以近似成一系列的衰減復指數之和，可以將時域信號表示為如下公式所示的形式。

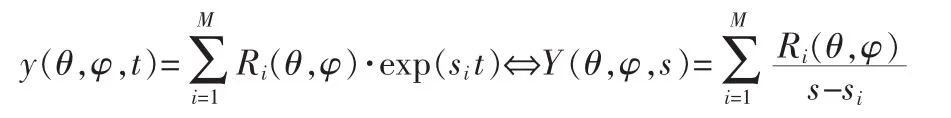
其中，y（t）是觀測時域信號；Ri是留數；Si可以表達為 σi+jωi，σi為衰減因子，ωi為諧振頻率。

在復頻域，信號的特性由極點（或稱奇點），留數等參數確定，極點的個數及大小與金屬導體的結構有關，與其它的外部因數和激勵無關。相應的留數，則與激勵的波形，入射波的入射方向，觀測的角度等參數有關。通過極點與留數，可以表征信號的衰減因子，諧振頻率，幅度，以及相位。由于極點是結構的基本屬性，與其它別的因數無關，從而可以通過極點的變化來映射結構的變化，可以通過極點來對導體標簽結構的識別，留數感知標簽結構的其它物理信息的功能。

1.2 極點的提取

目前，極點提取的辦法有prony法，矩陣束算法[5]等數學方法，矩陣束算法，與prony法相比較，具有低方差，高效等特點。其矩陣束法的基本思想是，將得到的數據信息轉化成矩陣的形式，并根據數據矩陣間的相互關系求解它們的廣義特征值，廣義特征值包含了所要求解的信息（信號的極點），因此，求解“衰減指數和”的信號模型的極點問題轉化為求解矩陣束的廣義特征值問題。通過數學公式的演算與推導，在一定的程度上，矩陣束算法得到的極點與留數有比較高的精度。

2 極點與留數的變化關系

2.1 入射方向或觀測的角度對極點與留數的影響

如圖1，開槽圓環型的標簽結構，其外圈的半徑r1=20 mm，次外圈的半徑r2=16 mm，最里圈的半徑r3=9 mm，開槽的寬度依次等間距，其中寬度w=9 mm。如圖1所示，對同一標簽結構，入射波的極化方式一樣（即極化的角度與入射傳播方向成90度），考慮不同的入射方向激勵標簽結構，激勵入射波與標簽結構XOY平面之間的角度依次為90度，75度，60度，45度，30度，15度。

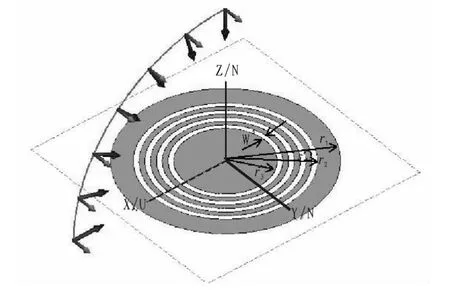
圖1 不同的入射角度激勵標簽結構Fig.1 Angle of incidence of different excitation to tag structure

通過電磁波仿真軟件FEKO，仿真得到其標簽結構的RCS（Radar Cross Section）數據，運用矩陣束算法提取極點。如圖2所示，在標簽結構與入射波的極化角度相同的條件下，不同入射角度所得到的主要極點近似一樣。

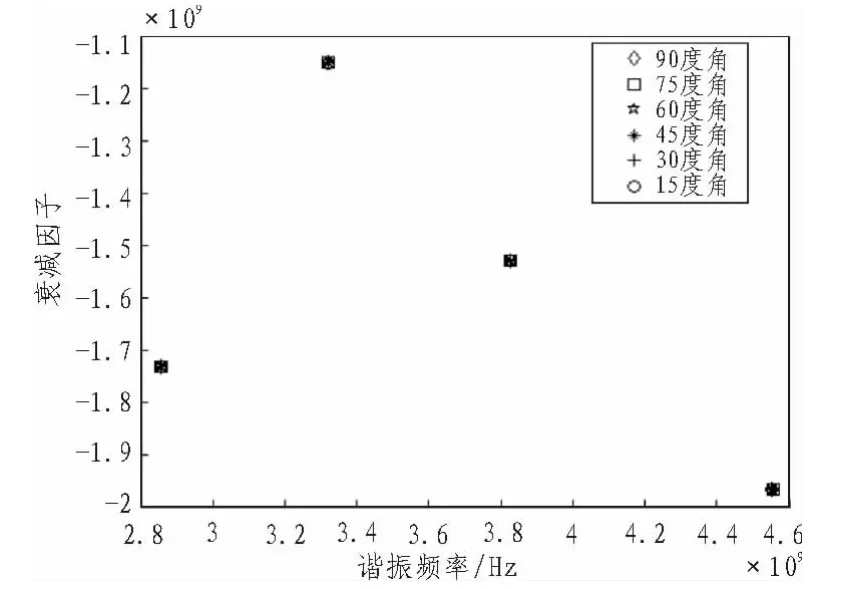
圖2 不同入射角度的極點分布圖Fig.2 Different incident angles of pole distribution

由開槽型結構所形成的諧振頻率，與槽的長度成反比關系，槽的長度越長，所成的諧振頻率值越小，相反，槽的長度越短，所形成的諧振頻率值就越高。

由極點與結構的開槽數成對應映射關系，可以通過極點的個數與相應的諧振頻率分布來設別標簽的開槽數與開槽情況。

與極點相應得留數，如圖3所示，在不同的入射角度下，留數呈現有規律的分布，隨著入射的角度變化，依次的變化，其留數的絕對值越小。不難理解，入射的角度越大，其標簽結構得到的散射信息的強度越低，而留數則可以表征這些極點幅度的強弱關系。

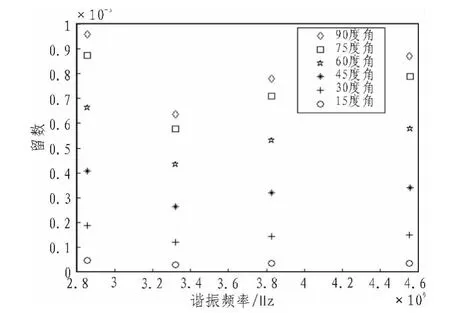
圖3 不同入射角度時留數分布圖Fig.3 Number of different angles of incidence of residue distribution

可以根據留數的相關信息可感知標簽結構應對入射波或觀測點的方位角度變化，進一步的對無芯片電子標簽識別。

2.2 不同的極化角度，對標簽結構的影響，極點與留數的關系

如圖4所示，標簽結構的尺寸與圖1中的尺寸一致，圖a，b，c分別表示在入射方向與標簽結構的中心位置成45度角時，不同的入射波極化角度，依次的極化角度為0度，30度，90度。

從圖5中大致的可以得到，在相同的標簽結構，相同的入射角度的條件下，不同的入射極化角度，其極點分布情況也近似一致。通過理論仿真分析可以得到，這種開槽圓環型的標簽結構，具有高度的對稱性，入射波的入射的角度，與入射波的極化角度，對主要極點的分布影響不大，在理想環境下，可以近似為一樣。

同樣，與極點相應的留數，如圖6所示，同樣隨著極化角度的變化而規律的變化，極化角度為0度時，相應的留數的值最小，極化角度為90度時，其留數的值最大。通過留數值的分布，反過來去感知標簽結構相對于入射波的極化角度。這樣可以通過留數值的變化情況，識別標簽結構的極化特性。

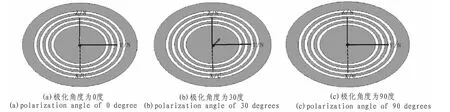
圖4 入射角度為45度時不同的極化角度Fig.4 Incident angle of 45 degrees angle of different polarization

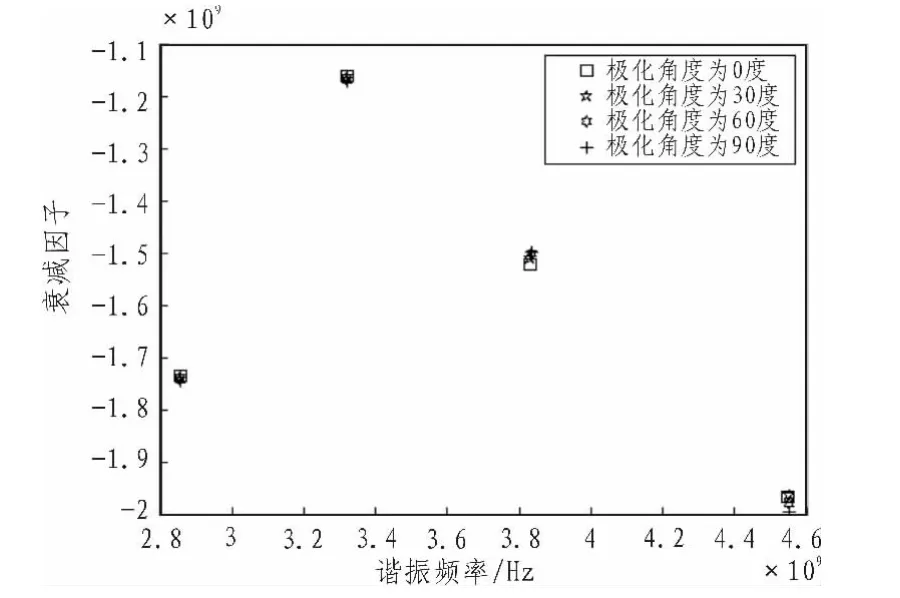
圖5 入射角度為45度時不同極化角度的極點分布圖Fig.5 When the incident angle is 45 degrees different polarization angles pole distribution

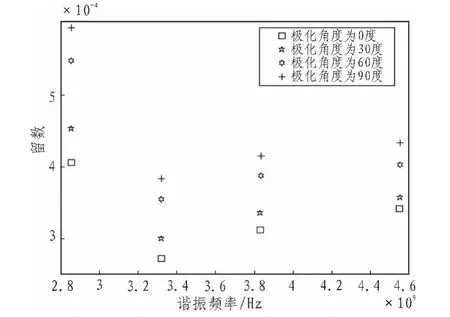
圖6 入射角度為45度時不同極化角度的留數分布圖Fig.6 When the incident angle is45 degrees different polarization angles residue distribution

2.3 彎曲形變的標簽對極點留數的影響

如圖7（a）所示，標簽結構在彎曲曲率半徑為30 mm的情況下的俯視圖，（b）為側視圖。標簽結構尺寸與開槽尺寸如圖1所示。

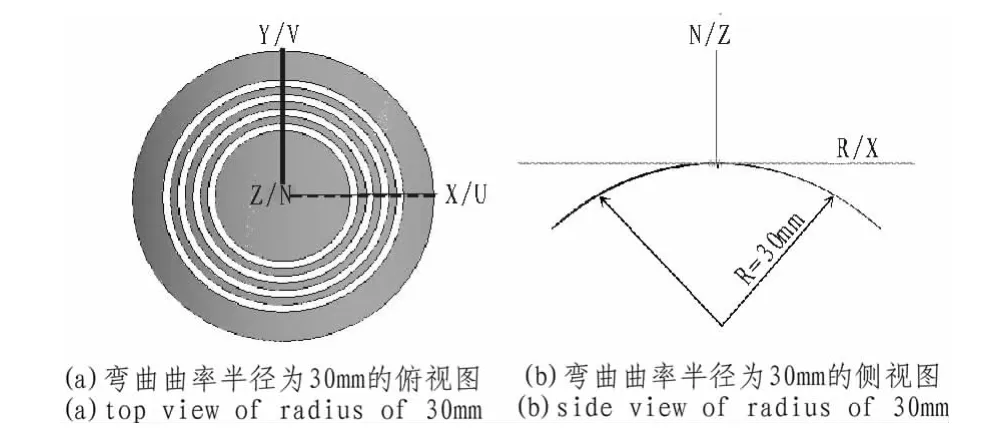
圖7 彎曲型標簽結構的示意圖Fig.7 diagram strncture of bendable label

標簽結構在不同的彎曲條件下，極點與留數分布情況，如圖8圖9所示。從圖8中可以分析到，標簽結構在不同程度上的彎曲，極點也會出現偏差而不同。由不同彎曲程度的標簽結構，標簽結構的基本屬性也隨之改變，極點中的衰減因子與諧振頻率之間的關系則可恰好可表征標簽結構的屬性特征。

從圖8可以得到，由于極點與留數共同表征信號，留數也隨之有規律的變化，隨彎曲半徑的增多，其留數也隨之變大。不難發現，平整平面時，標簽結構接受到激勵的有效單位面積越大，由RCS有關的定義與概念，其值與有效面積成正向關系，在散射場內，散射回的信號幅度越大。進而可以通過極點或留數的分布情況，識別與感知標簽結構的彎曲程度。

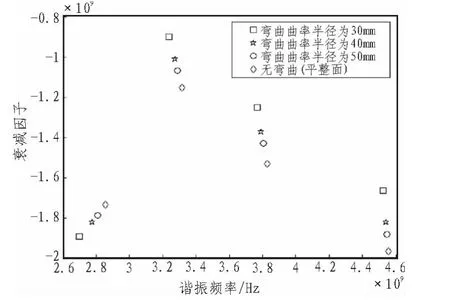
圖8 不同程度彎曲標簽結構的極點分布圖Fig.8 Varying degrees of bending the pole distribution label structure

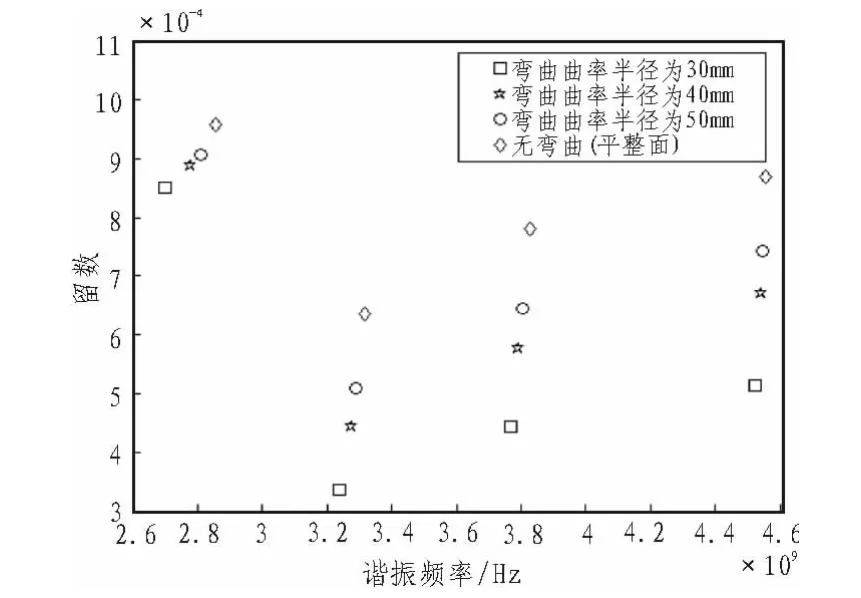
圖9 不同程度彎曲標簽結構的留數分布圖Fig.9 Structure of varying degrees of bend label residue distribution

2.4 入射波的極化特性對彎曲型標簽結構極點與留數的關系

對同一彎曲程度的標簽結構（彎曲的曲率半徑為30 mm時），相同的標簽結構尺寸，相同入射波，不同的入射極化角度，由于結構的對稱性，可依次取入射波的極化角度為0度，15度，30度，45度，75度，90度。

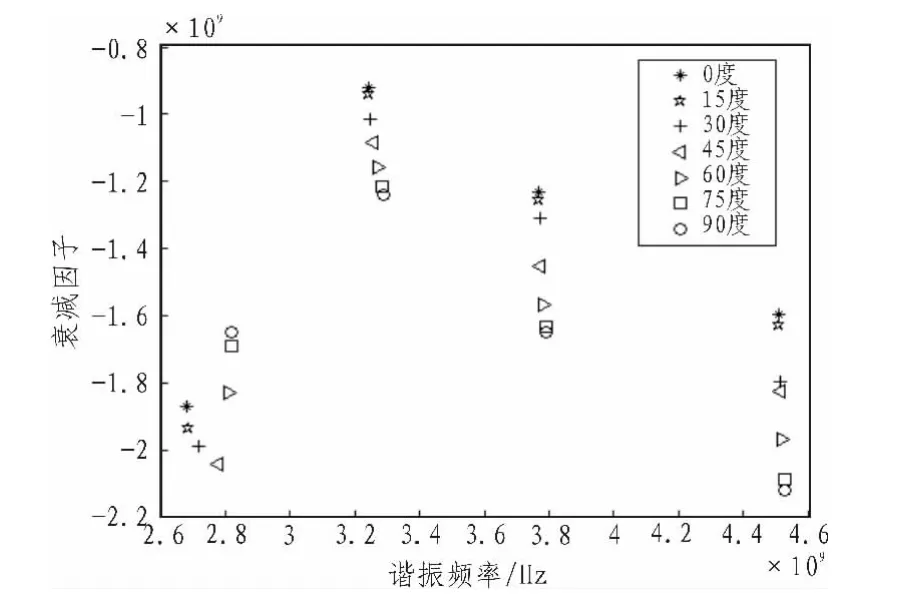
圖10 彎曲半徑為30 mm時極點分布圖Fig.10 Pole distribution of bending radius of 30 mm

對同一彎曲程度的標簽結構，極化角度的不同，極點與留數的分布情況如圖10與圖11所示，可以從圖10中大致的分析到，對諧振頻率在2.8 GHz附件的極點，在激勵波的極化角度為45度左右時，其衰減因子的絕對值為最大，相應的留數也會隨之變化，在激勵波的極化角度為45度左右時，其留數的絕對值存在最大值，這表明變形的標簽結構存在最佳激勵波的極化角度。可以通過極點或者留數這種變化關系，感知彎曲型標簽結構相對于入射波的極化特性。

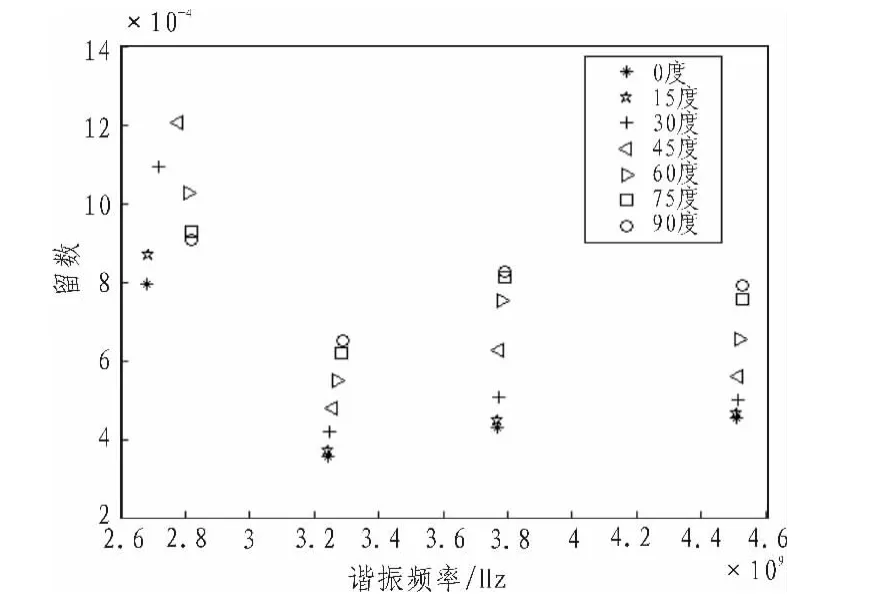
圖11 彎曲半徑為30 mm時留數分布圖Fig.11 Residue distribution of bending radius of 30 mm

3 結束語

這種開槽圓環型的標簽結構簡單緊湊，還具有高度的對稱性。通過極點的數據信息，可分析得到標簽結構的基本屬性，即開槽數以及開槽情況；還可以利用極點相對應的留數數據信息，感知標簽結構的其它特征屬性，即標簽結構相對于入射波或者觀測點的空間角度信息，標簽結構的彎曲變形程度等。很大程度上，極點或留數還能夠起到傳感標簽結構其它特性的作用。這種開槽圓環型的結構潛在成為一種具有感知傳感功能的無芯片電子標簽。

[1]KLAUS Finkenzeller，吳曉峰，陳大才譯.射頻識別技術[M].北京：電子工業出版社，2006.

[2]PRERADOVIC S，BALBIN I，KARMAKAR N C，et al.A novel chipless RFID system based on planar multiresonators for barcode replacement[C]//RFID，2008 IEEE International Conference on.IEEE，2008:289－296.

[3]ISLAM M A，KARMAKAR N.Design of a 16-bit ultra-low cost fully printable slot-loaded dual-polarized chipless RFID tag[C]//Microwave Conference Proceedings （APMC），2011 Asia-Pacific.IEEE，2011:1482－1485.

[4]VENA A，PERRT E，TEDJINI S.Chipless RFID tag using hybrid coding technique [J].Microwave Theory and Techniques，IEEE Transactions on，2011，59 （12）:3356 －3364.

[5]JANG H S，LIM W G，OH K S，et al.Design of low-cost chipless system using printable chipless tag with electromagneti c code [J]. Microwave and Wireless Components Letters，IEEE，2010，20（11）:640－642.

[6]PRERADOVIC S，KARMAKAR N C.Multiresonator based chipless RFID tag and dedicated RFID reader[C]//Microwave Symposium Digest （MTT），2010 IEEE MTT-S International.IEEE，2010:1520－1523.

[7]BAUM C E，ROTHWELL E J，CHEN K M，et al.The singularity expansion method and its application to target identification[J].Proceedings of the IEEE，1991，79 （10）:1481－1492.

[8]SARKAR T K，PARK S，KOH J，et al.Application of the matrix pencil method for estimating the SEM（singularity expansion method）poles of source-free transient responses from multiple look directions[J].Antennas and Propagation，IEEE Transactions on，2000，48（4）:612－618.

[9]王寶義，時振棟.電磁場在目標識別中的應用[M].北京：電子工業出版社，1995.

[10]BLISCHAK A T，MANTEDHI M.Embedded singularity chiplessRFID tags[J].Antennasand Propagation，IEEE Transactions on，2011，59（11）:3961－3968.