主點與旋轉中心距離的標定方法

李建榮，王志乾，王春霞，趙 雁

(中國科學院長春光學精密機械與物理研究所，吉林長春130033)

1 引言

光電測量方法是現階段應用最多的精密測量方法。廣泛應用于航天、航海、衛星測繪等國防建設以及工業制造和日常生活中［1－2］。光電測量系統種類繁多，許多跟瞄類光電測量系統都是把光學鏡頭固定在跟蹤架上對目標進行掃描和測量。跟蹤架有單軸、雙軸、三軸等幾種，因為單軸跟蹤架相對于多軸跟蹤架來說結構簡單、精度高等優點，所以單軸跟蹤架光電測量系統應用廣泛。在理想的單軸跟蹤架光電測量系統中光學鏡頭的主點與跟蹤架的旋轉軸重合，這樣有利于計算［3］。但是在實際應用中由于機械加工、光學加工、機械裝調、光學裝調等誤差，使得光學鏡頭主點很難與跟蹤架的旋轉軸重合。在遠距離測量時這個誤差不會對測量誤差帶來很大影響［4－6］，但是在近距離測量中這個誤差對測量結果的影響很大。

為了提高近距離光電測量系統的測量精度，消除光學鏡頭主點與旋轉軸之間距離帶來的誤差［7－8］，這就需要精確標定出這個距離，把標定出的距離值帶入測量系統中的計算式中進行誤差消除。本文論述了一種近距離光電測量系統中精確標定光學鏡頭主點和旋轉中心之間距離的方法。

2 光電測量系統的構成

2.1 光電測量系統的硬件構成

本光電測量系統主要由激光目標靶、伺服單元、編碼器單元、光學成像單元、CCD單元、處理單元等組成。其結構框圖如圖1所示。

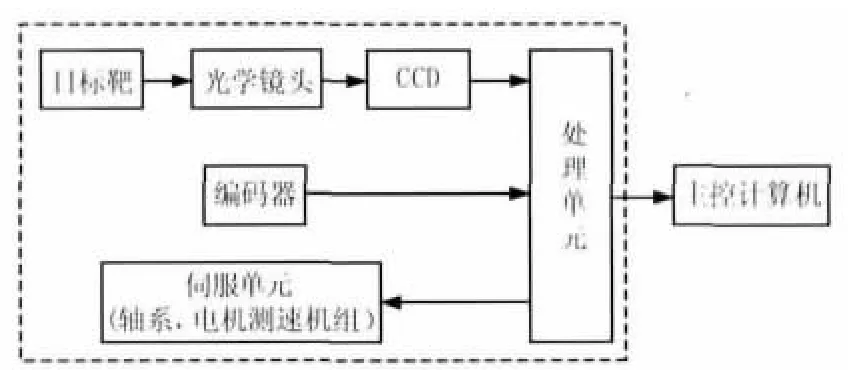
圖1 光電測量系統結構框圖

2.2 光電測量系統的工作原理

該光電測量系統的示意圖如圖2所示。測量系統的基本工作原理為:在系統開始工作時，處理單元首先根據讀取編碼器單元的位置信息，發送控制命令給伺服單元;伺服單元帶動光學鏡頭旋轉，使激光目標靶通過光學鏡頭成像;CCD單元接收激光目標靶的圖像信息;處理單元同時接收編碼器單元發送出來的位置信息和CCD單元發送出來的圖像信息，并對這些信息進行處理，最后得到所求的測量結果。并把此測量結果發送給上位機的主控計算機。

在圖 2 中，A1，A2，B1，B2是四個激光目標靶，O'為四個激光目標靶的幾何中心，O為軸系旋轉中心。以O'為原點建立如圖2所示的直角坐標系，利用激光目標靶之間的距離L，H，CCD接收到的激光目標靶的圖像信息，光學鏡頭的光學參數及編碼器的位置信息可以計算出圖2中O在坐標系中的三維坐標位置。

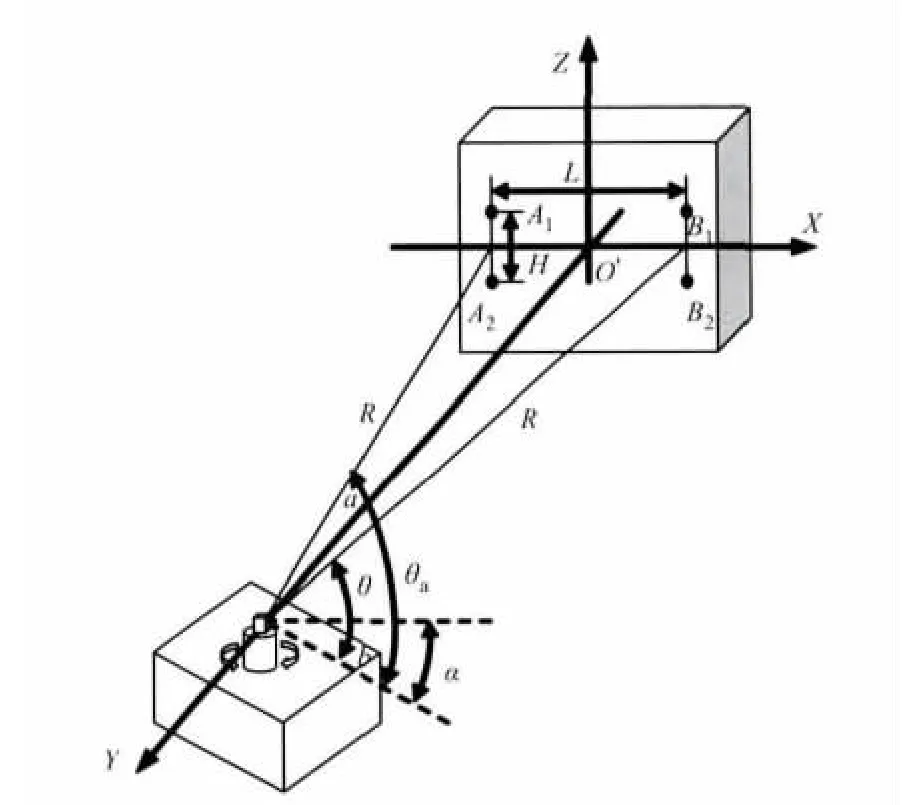
圖2 光電測量系統結構示意圖

3 主點的運動軌跡分析

3.1 一般情況下主點的運動軌跡

當光學鏡頭主點與軸系的旋轉軸不重合時，軸系旋轉會帶動光學鏡頭的主點運動。但是在近距離測量計算時光學鏡頭的主點是一個非常重要的測量基準，它的不斷運動會給測量帶來較大的誤差，為了消除這個誤差，需要對主點隨旋轉機構運動的軌跡進行分析［9］。本光電測量裝置是單軸旋轉平臺，當旋轉機構帶動光學鏡頭對目標架進行掃描測量時，光學鏡頭主點的運動示意圖如圖3所示。

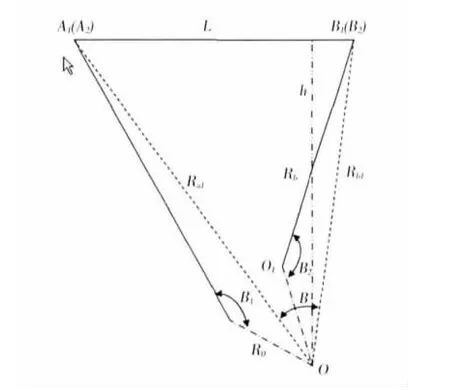
圖3 光學鏡頭主點運動示意圖

在圖3中，O為軸系的旋轉中心，當光學鏡頭掃描到目標靶B1(B2)時，光學鏡頭的主點在O1位置;當光學鏡頭掃描到目標靶A1(A2)時，光學鏡頭的主點在O2位置。圖3中的R0即為光學鏡頭主點到旋轉中心的距離。由三角理論可得下列計算公式:

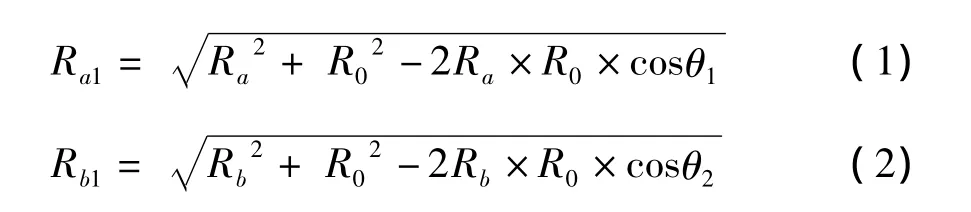
為了使表達式表示清晰，引入中間量s，s的表達式如下:

則h的表達式如下所示:

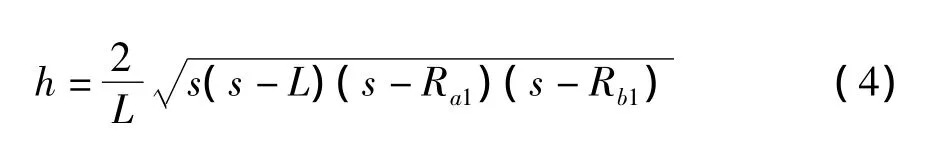
把式(1)，(2)，(3)帶入公式(4)得到h的完整表達式如下:

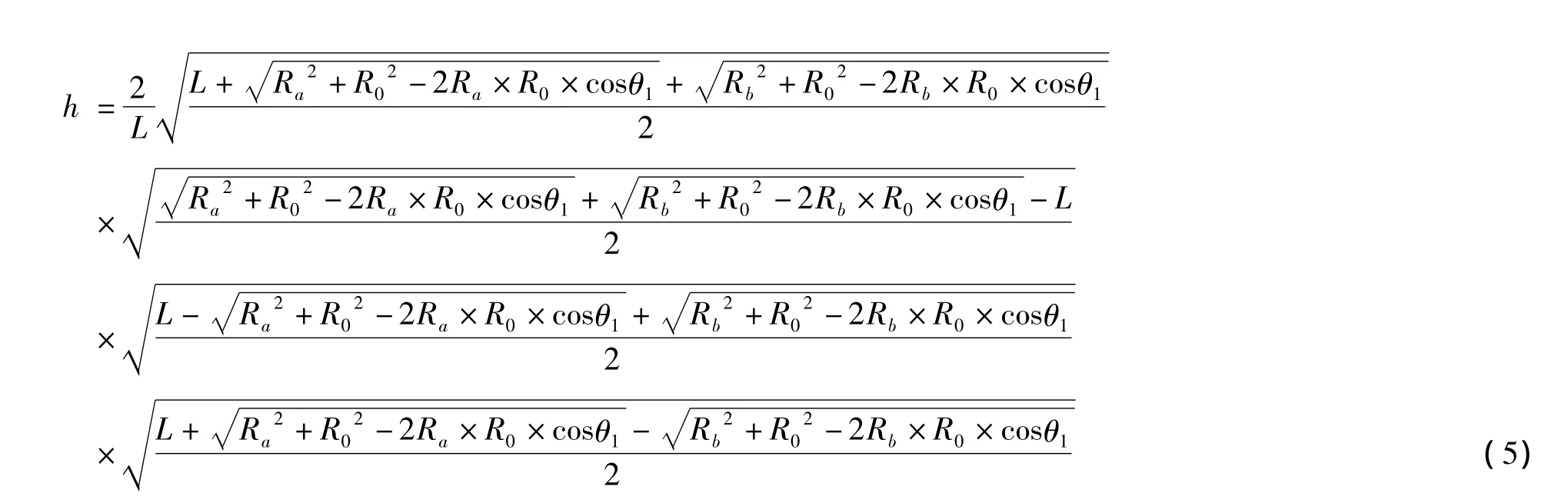
由式(5)可知，光學鏡頭主點到旋轉中心之間的距離R0是角度θ1的函數。但是按照這個表達式進行補償，計算過程很復雜，利用嵌入式系統進行實時處理很困難。這對實時性要求很高的嵌入式系統來說是一個嚴重的缺陷。為了使計算簡單，在工程實際中，可以在光學鏡頭的裝調過程中，利用對稱性，使光軸和旋轉中心線相交與一點，這會使計算過程得到極大的簡化，滿足嵌入式系統的處理要求。

3.2 共面情況下計算公式的推導

當光學鏡頭的光軸和旋轉機構的旋轉軸線相交于一點時，圖3主點運動示意圖可以簡化為圖4。如圖4所示，O為旋轉中心，旋轉機構帶動光學鏡頭逆時針旋轉。當光學鏡頭掃描到目標點B1(B2)時，主點的位置在O1，當光學鏡頭掃描到目標點A1(A2)時，主點的位置在O2。

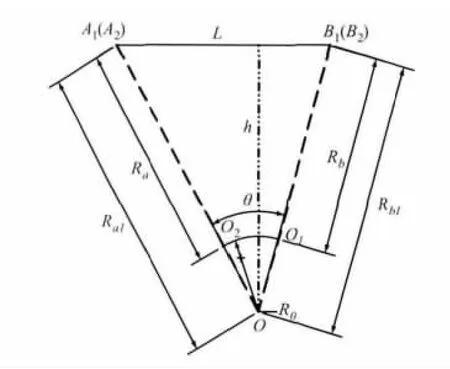
圖4 光學鏡頭主點運動簡化示意圖

由光電編碼器可以測得旋轉的角度值為θ，由交匯測量系統建立的空間直角坐標系可以測得B1(B2)到A1(A2)的距離為L。從CCD接收到的B1(B2)的圖像信息可以計算出O1到B1(B2)的距離(物距)Rb。同理可以計算出O2到A1(A2)的距離(物距)Ra。h的計算公式就是公式5中當180°的h表達式，具體如下:

在公式(6)中，h，L的長度可以由交匯測量系統測得。Ra，Rb可由線陣 CCD采集的A1(A2)和 B1(B2)圖像計算得到，所以這些都可以看成是已知量。所以可以得出光學鏡頭主點到旋轉中心之間的距離R0的值。可以看出公式(6)要比公式(5)的計算量少很多，能夠應用嵌入式系統進行實時處理。

在圖4中，由光電編碼器可以測得角度θ，所以h與R0的關系式還可以表示為如下形式:

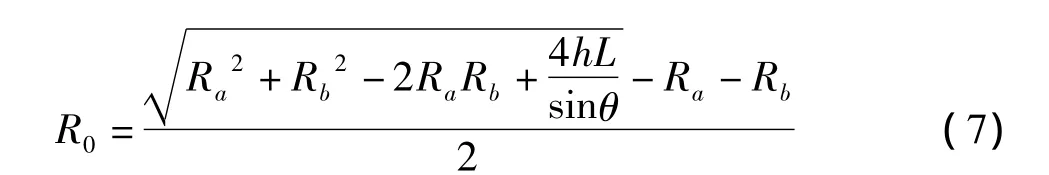
可以看出公式(7)比公式(6)的計算更簡單，計算量更少，更有利于處理器處理，所以在本實驗的標定過程中用的就是此種表達式。

4 測量實驗與結果

為了檢測本標定方法的效果，做了大量試驗對本方法進行檢測驗證。某次試驗選用焦距為30.09 mm的光學系統進行了R0的標定試驗。用交匯測量系統建立空間直角坐標系，坐標系的精度為0.01 mm。用此直角坐標系對公式(7)中h，L，H的值進行標定，標定精度為0.05 mm;利用位置檢測裝置對目標架進行測量，得出公式(7)中的物距Ra，Rb的測量值和它們的夾角θ的角度值。并根據公式(7)求解方程計算出R0的值。在9個位置進行測量，得到的9組實驗數據如表1所示。

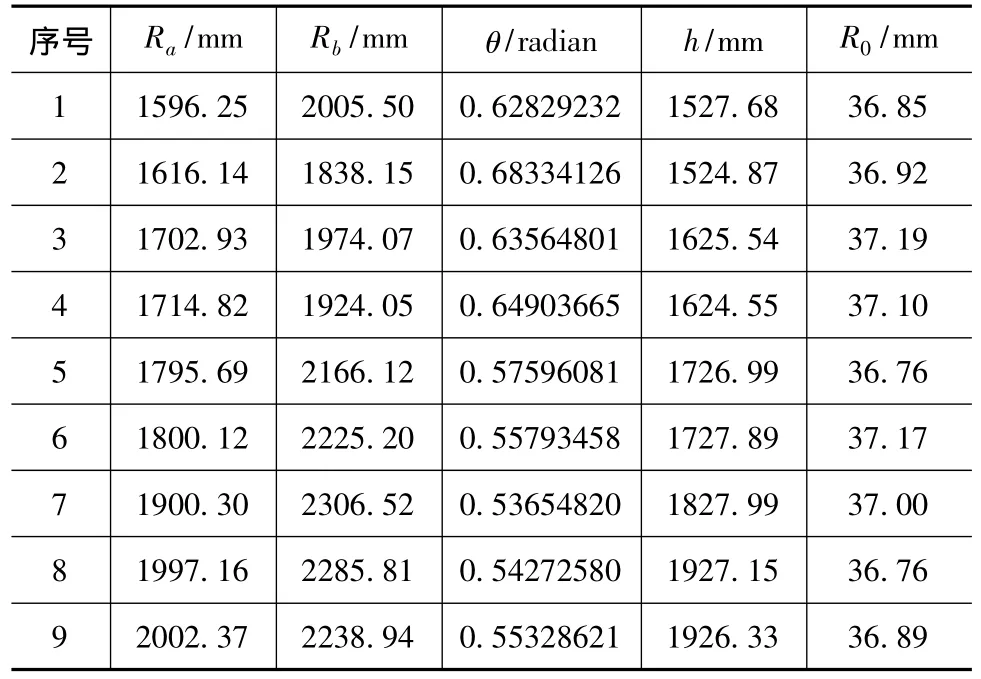
表1 R0實驗測量數據表

在表1中R0的加權平均值為。由此可見R0的標定精度可達0.23 mm，把R0帶入公式進行補償后，能夠減小R0帶來的測量誤差，提高非接觸式位置檢測裝置的測量精度。

5 結論

本文通過對光學鏡頭主點到旋轉系統旋轉軸線距離的分析，建立了主點與旋轉中心之間距離的數學模型，提出主點與旋轉中心之間距離的標定方法。最后根據此測量算法進行了實驗測量，得出實驗測量數據，并對此數據進行了分析，實驗結果表明，該方法的標定精度為0.23 mm，對提高本光電測量系統的測量精度有重要的意義。同時精確標定主點與旋轉中心之間的距離，對近距離光電測量系統測量精度的提高具有實際的參考意義。

［1］ Fu Yun，Zhang Xun，Wu Keyong.Application of non-contact rendezvous measurement to spatial position measurement［J］.Opto-Electronic Engineering，2005(9):39 －42.(in Chinese)付蕓，張峋，武克用.非接觸交匯測量法在空間位置測量中應用［J］.光電工程，2005(9):39－42.

［2］ Wu Lushen，Liu Zhen，Wu Peimin，et al.Design of face detection system based on embedded video monitor［J］.Laser＆ Infrared，2012(2):231 －234.(in Chinese)吳祿慎，柳珍，吳培敏，等.基于嵌入式視頻監控的人臉檢測系統設計［J］.激光與紅外，2012(2):231－234.

［3］ Wang Zhen，Shen Gongxun.Investigation on integral method of pendulous gyroscope［J］.Optics and Precision Engineering，2007(5):746 －752.(in Chinese)王縝，申功勛.擺式陀螺尋北儀的積分測量方法［J］.光學 精密工程，2007(5):746－752.

［4］ Xu Jianhua，Liu Xingqiao，Chen Jiabin.Strap-down north finder azimuth error analysis［J］.Acta Armamentarii，2006，27(2):284 －287.(in Chinese)徐建華，劉星橋，陳家斌.捷聯尋北儀方位角誤差分析［J］.兵工學報，2006，27(2):284 －287.

［5］ Cui Sumei，Zhao Meirong，Song Le.Infrared image edge extraction based on fuzzy neural network［J］.Laser＆ Infrared，2012(9):1064 －1067.(in Chinese)崔素梅，趙美蓉，宋樂.基于模糊神經網絡的紅外圖像邊緣提取算法［J］.激光與紅外，2012(9):1064－1067.

［6］ Zhang Lianchao，Fan Shixun，Fan Dapeng，et al.Research and implementation of digital control of dynamically tuned gyroscope rebalance loop.Optics and Precision Engineering，2007(12):1974 －1981.(in Chinese)張連超，范世勛，范大鵬，等.動力調諧陀螺再平衡回路數字化的研究與實現［J］.光學 精密工程，2007(12):1974－1981.

［7］ Li Yan，Zhang Zhiyong，Fan Dapeng.Principle of the effect of gyro misalignment on the stabilization platforms accuracy［J］.Opto-Electronic Engineering，2007(9):10 －15，29.(in Chinese)李巖，張智永，范大鵬.陀螺安裝誤差影響視軸穩定平臺精度的機理研究［J］.光電工程，2007(9):10 －15，29.

［8］ Liang Zhiguo，Zhang Dazhi.A fast arithmetic method of four-parameter sine wave curve-fit［J］.Aviation Metrology＆ Measurement Technology，2006，26(1):4 －7.

［9］ Ren Shunqing，Zhao Zhenhao，Chen Yan.Error analysis for the gyro north seeking system［C］//ISSCAA，Harbin，2006:783－786.