等高線綜合方法的比較與分析

胡 菡，陳春華,2，孫 霞

（1.湖北省測繪工程院，湖北 武漢 430074；

2.精密工程與工業測量國家測繪地理信息局重點實驗室，湖北 武漢 430079）

等高線綜合方法的比較與分析

胡 菡1，陳春華1,2，孫 霞1

（1.湖北省測繪工程院，湖北 武漢 430074；

2.精密工程與工業測量國家測繪地理信息局重點實驗室，湖北 武漢 430079）

從制圖綜合的約束條件著手，針對等高線的自動綜合方法進行研究。提出了等高線綜合算法的比較方法，制定出一套等高線綜合方法的評價指標并進行了實驗，從幾何約束、拓撲約束、結構約束等方面驗證了這套方法和指標的合理性和可行性。

等高線自動綜合；約束條件；道格拉斯算法；算法比較

本文對幾種有代表性的等高線綜合方法進行比較，尋找各自特點，討論并得出等高線綜合方法評價的方法和標準。

1 等高線綜合算法的比較方法

制圖綜合中的約束源于綜合控制中的要素。本文力圖通過對制圖綜合約束條件的分析來建立評價指標，以判斷等高線綜合算法的可靠性和適用性。一般情況下，約束條件可以分為幾何約束、拓撲約束、結構約束和格式塔（Gestalt）約束等幾類。

1.1 幾何類指標

1）等高線點位精度

等高線的位置精度對地形圖而言相當重要，其衡量標準定義為抽樣點在綜合前的位置到該點所在原始等高線綜合后得到的等高線的最短距離。

2）等高線長度比

一般而言，綜合后的等高線長度會小于綜合前。對于同一根等高線而言，其長度在綜合后越小，說明綜合程度越大。因此，在某些參數相同的情況下，可以通過等高線綜合前后的長度比，從側面反映算法的綜合程度。同時，也可以通過等高線長度比的變化，衡量等高線綜合算法的合理性及算法的穩定性。

1.2 拓撲類指標

1）拓撲信息量

等高線之間存在的嚴格的序關系，被視為等高線的拓撲關系，可以用等高線樹來表示。可以把閉合的等高線看成面，對于不可能相交的等高線而言，其構成的面與面之間的拓撲關系主要有包含、相離兩種。將這種拓撲關系表現成樹結構，則可將包含關系定義為父子關系，而相離關系定義為并列關系。

在此基礎上，就可以對等高線的拓撲信息量進行量算。假設等高線樹中等高線Ci有Ni個鄰居結點，根據鄰居結點個數對結點進行分類：有1個則屬于分類1，有2個則屬于分類2，…。設Ci的鄰居共屬于Mi種分類，第j類鄰居共有nj個，則第j類鄰居出現的概率為：

等高線Ci的拓撲信息量為：

2）拓撲錯誤數量

等高線自動綜合中的拓撲錯誤主要包括等高線的自相交、自重疊以及與相鄰等高線之間的相交、重疊等。

1.3 結構類指標

1）地形結構

綜合前后制圖區域的地形結構能否得到保持，是衡量等高線綜合算法的一項重要指標。本文通過分析提取出的匯水線的相似程度，來判斷等高線綜合算法在地貌形態結構保持方面的優劣。

2）等高線高程分布

通過對等高線的高程信息，如高程極大值、極小值、算術平均值、標準差等的比較、分析，可以判斷出不同等高線綜合算法對高程數據的保留是否合理。

格式塔及其他指標包括等高線光滑程度、數據壓縮程度、算法化簡時間等，這里不一一說明了。

2 實驗分析

選擇我國南方某地作為實驗樣區。根據等高線的形態和地形的平坦程度，選取了兩塊數據區域，大小均為1 500 m×1 500 m，平均高程分別為289.581 m和214.763 m，等高距5 m。

實驗選用Douglas-Peucker算法和三維Douglas-Peucker算法進行比較，它們分別屬于二維、三維以及直接、間接等高線綜合方法，具有較強的代表性。實驗在保留相同的特征點數下進行，以保證其他指標比較時的公平性。

兩塊實驗樣區的原始數據以及二維道格拉斯、三維道格拉斯算法綜合后的數據如圖1所示。

圖1 樣區綜合前后等高線圖

2.1 點位精度

分別從兩塊數據中選取30個樣點，通過量算、統計，得到這60個抽樣點的偏移量。根據比較，綜合前后點位的偏移量，二維道格拉斯算法較三維道格拉斯算法普遍小。另一方面，三維道格拉斯算法綜合前后點位偏移量的標準差較二維道格拉斯算法偏大，說明三維道格拉斯算法在點位精度保持上的穩定性較差。

2.2 等高線長度比

對二維道格拉斯算法而言，所有的長度比均小于1，即綜合后等高線長度較綜合前要小，這符合一般規律。對三維道格拉斯綜合算法而言，絕大部分長度比小于1，但抽樣數據中也有一根等高線綜合前后長度比略大于1。從等高線長度比的方差得出，二維道格拉斯綜合算法得到的等高線長度比較穩定；三維道格拉斯綜合算法得到的等高線長度比不僅存在大于1的可能，而且其在平均值附近擺動的幅度遠大于二維道格拉斯算法。

2.3 拓撲信息量

分析綜合前以及用兩種算法綜合后的兩塊實驗數據的等高線圖，得到如圖2所示的兩組等高線樹。

圖2 樣區綜合前后等高線樹

在等高線樹基礎上對等高線的拓撲信息量進行了量算，如表1和表2。

表1 拓撲信息量偏差統計

表2 總體拓撲信息量統計

由表可知，對于二維道格拉斯綜合算法，無論是單根等高線拓撲信息量，還是等高線圖的總體拓撲信息量，均沒有變化。而三維道格拉斯算法的拓撲信息量有較大的改變，這主要是因為三維道格拉斯算法針對整個制圖區域的地貌形態進行綜合，而后內插生成新的等高線，內插過程中難免會造成等高線拓撲關系的變化。

2.4 拓撲錯誤數量

三維道格拉斯綜合算法在本次實驗中沒有出現等高線相交、重疊或其他拓撲錯誤。而二維道格拉斯綜合算法在兩塊實驗數據的綜合結果中出現等高線自相交、自重疊各1次。

2.5 地形結構

分別將綜合前后實驗數據轉換為格網數據，生成矢量的河網數據，并對其進行統計和量算，得到河網分級情況及各級河流長度，如表3。

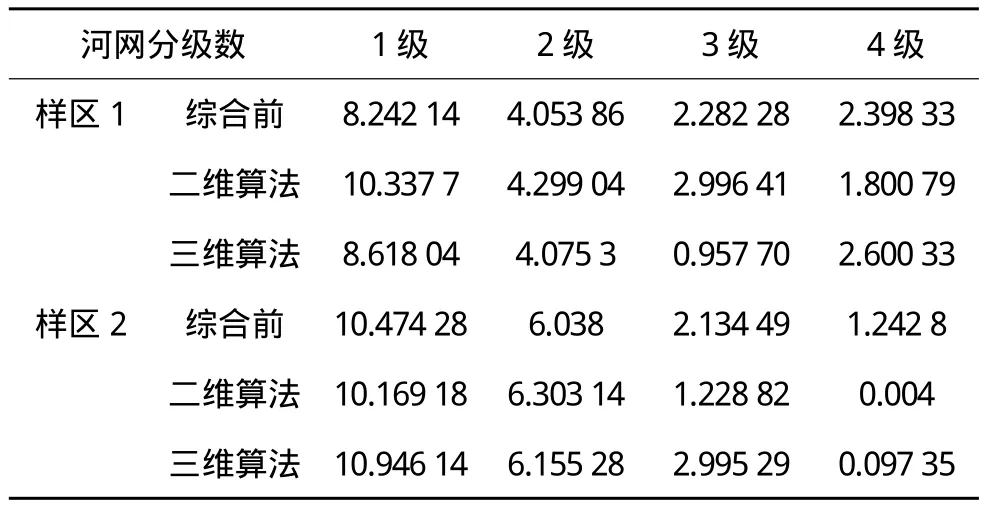
表3 河網分級統計/km

下面對河網分級數據進行分析和比較。以綜合前的河網分級數據為標準，計算二維和三維道格拉斯算法綜合后的河網分級情況與綜合前河網分級情況的偏差，來比較兩種綜合算法對地形結構的保留情況，如表4所示。

表4 河網分級偏差統計/km

從表4可以明顯看出，三維道格拉斯算法對地形結構的保持較二維道格拉斯算法好，兩塊實驗數據的河網分級偏差均較二維算法小。三維道格拉斯算法在地形結構保持方面明顯優于二維算法，這也非常符合三維道格拉斯算法從整體地貌綜合出發的特點。

2.6 高程分布

通過實驗比較得到的高程信息分布情況如表5。

可以明顯看到，用三維道格拉斯綜合算法綜合得到的等高線特征點數據與綜合前的原始數據的高程信息分布相當接近；而二維道格拉斯算法綜合得到的等高線數據與原始數據的高程信息分布差別則較大。這說明在高程信息的保留方面，三維道格拉斯綜合算法有明顯的優勢。

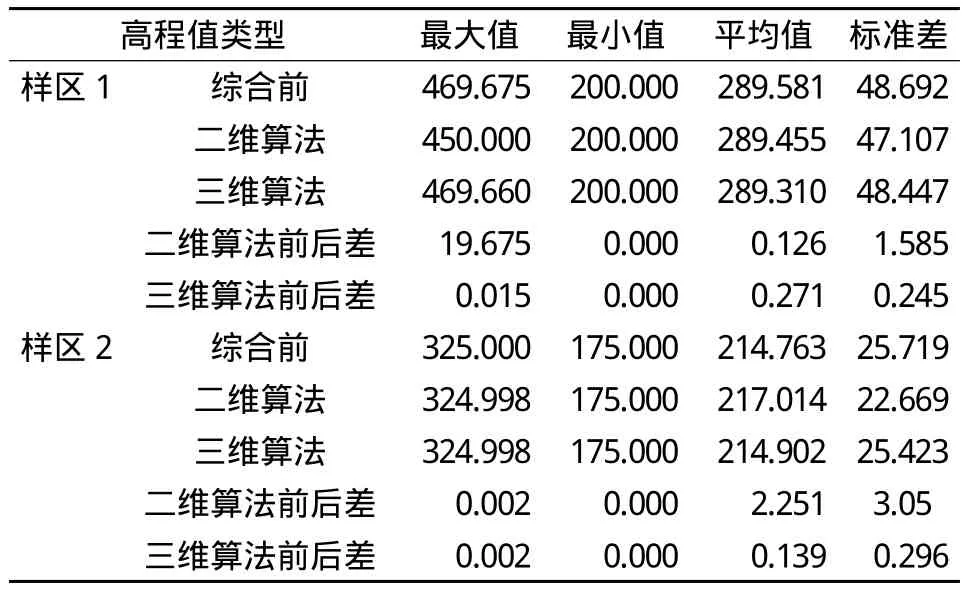
表5 高程信息統計/m

2.7 數據壓縮程度、等高線光滑程度

采用單根等高線在綜合前后的點數比衡量等高線光滑程度。三維道格拉斯算法在保留了地形特征點后內插生成的等高線，較二維算法從原始等高線上保留特征點直接生成的等高線光滑。但這也從一個側面反映出，要保持等高線光滑，其數據量必定較大。但三維道格拉斯算法在保留了地形特征點后，可利用不同的內插方法控制等高線上點的疏密，以達到控制數據量、等高線光滑程度等目的，靈活性大。

2.8 算法耗時

通過實驗比較得出，二維道格拉斯算法綜合等高線所花的時間明顯長于三維算法，可以認為三維道格拉斯算法綜合效率更高。

3 結 語

本文從制圖綜合的約束條件著手，建立了一套等高線自動綜合方法的比較指標。從實驗結果來看，這套指標可以反映不同等高線綜合方法的特點及其在各方面的優劣。實驗結果符合算法的特性，反映了這套比較指標的合理性和可行性。但在等高線綜合方法的比較研究方面，仍有大量工作有待探討，如建立合理的數學模型以更全面、更精確地對各項指標進行度量；探索對各項指標進行綜合評價的模型與方法；尋求量化格式塔約束的合理方法；通過比較有針對性地改進綜合算法。

[1] Fei Lifan, Huang Lina, He Jin. An Indirect Generalization of Contour Lines Based on DEM Generalization Using the 3D Douglas-Peucker Algorithm[C]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing, 2008

[2] 郭慶勝,毋河海,李沛川.等高線的空間關系規則和漸進式圖形簡化方法[J].武漢測繪科技大學學報,2000,25(1)：31-34

[3] 艾廷華,祝國瑞,張根壽.基于Delaunay三角網模型的等高線地形特征提取及谷地樹結構化組織[J].遙感學報，2003，3(4)：292-298

[4] 查正軍.基于數字高程模型（DEM)）的地形特征提取[D].上海：同濟大學，2007

[5] 李麗,郝振純.基于DEM的流域特征提取綜述[J].地球科學進展，2003，18(2)：251-256

[6] 朱鯤鵬,武芳.基于約束條件的線要素化簡算法質量評估[J].測繪科學，2007，32(3)：28-30

[7] 劉文鍇,喬朝飛.等高線圖信息定量度量研究[J].武漢大學學報：信息科學版，2008，33(2)：157-159

Comparisons and Analysis of Contour Lines’ Generalization Method

byHU Han

Based on constrain condition of cartographic generalization,this paper set out to study the generalization methods of contour lines. And then, the paper raised the comparison method of contour lines’ generalization algorithm, and formulated a series of evaluation indicators of it, verifying the rationality and feasibility of the method and indicators in geometric constraints aspect, topological constraints aspect, structure constraints aspect by experiments.

generalization of contour lines, constraint condition,Douglas-peucker algorithm, algorithm comparison

P283.1

B

1672-4623（2014）02-0141-03

10.11709/j.issn.1672-4623.2014.02.051

2013-05-31。

項目來源：精密工程與工業測量國家測繪地理信息局重點實驗室開放基金資助項目（PF2011-30）。

胡菡，研究方向為地圖數據處理及其理論研究，數字城市和地理信息系統應用與開發。