解題架橋 促進思維 培養能力

☉江蘇省揚州市邗江中學 倪富春

解題架橋 促進思維 培養能力

☉江蘇省揚州市邗江中學 倪富春

“注重提高學生的數學思維能力”確定為高中新課程的基本理念之一，因此，培養學生的數學思維能力也就顯得十分重要.在教學中如何實現這個理念，是一線教師一直追尋的目標.數學問題是數學的心臟，所以，在我們大量的數學問題教學中，要隨時善于利用一些解決問題的常用數學思想方法來培養學生的思維能力.下面舉例說明.

一、消除思維定勢，培養學生數學思維的靈活性

思維定勢是指影響或決定同類后繼心理活動的趨勢或形成心理活動的準備狀態，即人們用一種固定的思維習慣去考慮問題，表現為人們思維的一種趨向性和專注性.雖然思維定勢有助于學生運用學過的知識和積累的經驗去解決問題，但它也表現出思維的刻板和惰性，妨礙學生靈活性和創造性思維的發展.

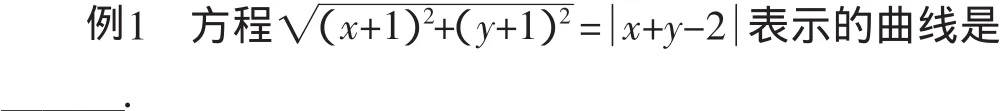
分析：欲通過化簡方程，與常見曲線方程對比，得出曲線形狀；但運算量大，結果也并不直觀，顯然，這種做法不可取.本題中，學生沒有注意到方程的特點以及蘊含的幾何含義，并忽視了圓錐曲線的統一定義.這暴露出了學生思維定勢，簡單僵化，缺乏靈活性.

由圓錐曲線的統一定義知，平面上動點到一定點與到一定直線的距離之比是一個常數，當這一常數大于1時，動點軌跡為雙曲線.

點評：思維的靈活性即善于全面地、科學地考察問題、分析問題，從各種事物的各種聯系中去認識事物.思維比較靈活的學生，不僅能夠把握住事物的全體，抓住事物的基本特征，而且也不會忽視重要的細節問題.

二、注重一題多解，培養學生數學思維的廣闊性

對于教學中的例題，引導學生一題多解，挖掘題目本身蘊含的教學價值，從而培養學生思維的廣闊性.

例2“若x，y為正實數，且滿足：xy-2x-y=1，求2x+y的最小值.”

這兩種方法有異曲同工之妙，都是利用基本不等式，可以轉化成2x+y，也可以轉化成xy，還有沒有其他的方法呢？在學生的熱烈討論之后，又得出了幾種解法：

這樣一道平常的題目就有四種解法，事實上學生的想法和思路是很多的，我們平時上課不能壓抑學生的想法，應該多花點時間讓學生自主思考，自主討論，各抒己見.通過這樣的一題多解，一方面，學生不僅可以看到知識之間的聯系和溝通，他們也將學會如何思考問題，將陌生的問題轉化成熟悉的問題，充分調動學生所學過的知識和方法，這也是我們常說的“舉一反三、觸類旁通”，對培養學生思維的廣闊性有很大的幫助.

三、關注隱含條件，培養學生數學思維的嚴密性

點評：思維的嚴密性表現為思維過程服從于嚴格的邏輯規則，考察問題時嚴格、準確，進行運算和推理精確無誤.

在三角函數的學習中，學生經常會忽視三角函數的有界性、已知條件中的隱含條件等問題.另外在對參數的分類討論、根與系數關系的應用（需要考慮判別式）、求函數的極值（需要檢驗左右兩側導數符號）等問題中，一些學生也往往會出現疏忽遺漏.這要求我們在平時的教學中，充分暴露學生的錯誤表現、思維障礙，引導學生關注隱含條件，發現錯誤，自主評價，并輔之適當的針對訓練，如此才使學生既能鉆的進去，又能跳的出來.從而，避免丟三落四、疏忽遺漏，達到培養學生思維嚴密性的目的.

四、加強解題后的反思，培養學生數學思維的批判性

例4 已知直線l過不同的兩點A（cosθ，sin2θ），B（0，1），求直線l的傾斜角α的取值范圍.：當生1說出答案時，一些同學便認為正確，思維被生1同化；當生2開始質疑時，又有很多同學開始贊賞，思維又被生2同化.這道題雖不難，但卻隱藏著“陷阱”，很多學生出現了失誤.這些同學在解題后沒有能夠及時反思，這暴露出他們思維缺乏批判性.

點評：批判性思維指的是對別人的觀點或自己原有觀點進行反思，提出質疑并有所創新的思維，其核心在于反思.為了培養學生這種批判性思維，除了建立民主平等的師生關系、鼓勵學生主動反思和質疑外，還要求教師在習題教學中，注重對錯誤的辨析、溯源、糾正和反思，特別是典型的、隱蔽的錯誤.

總之，對于學生解題中出現的思維障礙，我們分析出現障礙的原因，結合教學實際，千方百計地引導學生突破這些障礙.在平時教學中，我們應立足課本，對課本典型的例習題進行演變、探究、引申、拓廣、應用；由點到面，舉一反三，解剖一例，學會一類.解題中注意數學思想方法的滲透，注重基礎知識的演練，培養思維品質，發展思維能力.