凸顯核心——初中數學概念教學的突破口

☉江蘇省東海縣安峰初級中學 郄利霞

凸顯核心
——初中數學概念教學的突破口

☉江蘇省東海縣安峰初級中學 郄利霞

數學教學，必須重視數學概念及其滲透的思想方法，即抓住核心概念和概念的核心來組織教學，揭示其蘊含的思想方法.如果違背這個原則，僅僅把解題方法作為教學核心，以大量的練習題來應對概念教學，強化概念的內涵和外延，這在理解與做法上，都是片面的，教學是無效的.本文對概念教學中存在的缺失進行探討，并對如何理解概念的本質、構建數學認知結構以及掌握數學思想方法等幾個方面，進行全方位的探討，希望能給大家有所啟迪或借鑒.

一、忽視“核心”，數學概念教學的缺失

理解與掌握數學概念，是數學學習的前提與基礎.從新知學習到鞏固應用，從推理到判斷，學生對數學概念不熟悉或模糊不清，就無法進行，所以概念教學非常重要而必要.

目前比較常用的數學概念教學環節為：第一步，列舉數學最為熟悉的事例，或者設計前后知識的聯系，引入概念；第二步，學生對概念進行探討，形成概念；第三步，按定義舉出實例，讓學生舉出實例，明確概念；第四步，通過反例等對概念進行辨析和鞏固，明晰概念；第五步，練習強化，把握數學概念的本質，應用與鞏固概念.

然而，教學中，個別老師卻認為，上述環節中第五步是重心，即強化練習，培養學生的解題能力，其他如第一二步都是教學形式，可有可無.這種認識最終造成學生對數學概念的來源與背景不清，對概念的形成過程沒有體驗，無法適應新的概念，也沒有完成同化或順應、平衡，認知上存在嚴重缺失.具體表現在以下幾點：

1.缺少概念的形成過程，直接將數學概念的定義交給學生

如學生對“數的絕對值”概念的學習，已有的知識經驗是數的正負性和數軸概念.教學實踐中，經常有學生說“負數的絕對值是一個正數”或者“一個數的絕對值就是去掉符號”或者“就是不考慮數的正負性”，從表面上來看，這些都是學生對原有定義的改組并用自己的語言表述了絕對值概念，但這種改組偏離了概念本身的內涵，因此建立在這種表述上的認識還不能算是正確的理解，因為當用字母來表示數時，用上述解釋就很難做出正確的判斷.由數在數軸上對應的點到原點的距離來解讀數才是對數的絕對值概念的理解.課本例題如下：一輛汽車在東西方向的道路上行駛，規定向東為正，出發地為原點，然后來回地行駛，并最終停在某處，總共行駛了多少路程？這里就是絕對值的和，也就是無須考慮行駛方向.從本例出發來解析數的絕對值才真正有助于學生理解絕對值概念.“正數的絕對值是其本身，負數的絕對值是其相反數，零的絕對值是零”，讓學生掌握了求一個數的絕對值的方法.

2.缺少概念建立的體系，無法理解概念

概念體系的建立，與新舊知識的關系較大，但個別教師缺少這個環節.比如個別教師在設計教學時，往往會考慮某一點知識，可能出現“就事論事”或“見木不見林”的現象，沒有把知識體系當成核心，圍繞這一核心去組織教學.比如教學“0”的認識，在小學已經學習過，它表示“沒有”，有0個蘋果、0支鉛筆等，但在初中數學中的給“0”賦予了新的內容，0不再表示沒有，也可能表示溫度為0℃；也可能表示海拔為0米.

3.忽視概念教學時的“核心”，沒有分清教學的主次

比如，在統計與概率相關概念的教學中，多停留在計算的層面，如“平均數”和“概率”等概念的教學，缺少對其相關數據的分析，實際上計算并非重點，對相關數據的分析才是本單元概念教學的重點.

二、抓住“核心”，數學概念教學的突破口

1.把握“概念的核心”，讓學生理解概念本質

恩格斯強調：“數學就是關于客觀世界數量關系和空間形式的科學”，所以，在數學教學中要抓住關于空間形式與數量關系的關鍵點，即數學概念的核心，這是學好數學概念的前提.一般而言，把握數學概念的核心屬性，強調在問題情境中，引發學生的學習動機，設置一系列與概念有關的問題串，在探究中揭示概念的核心，去除影響概念核心的其他因素，從而理解概念的定義，理解其本質.

比如在教學“函數”這一概念時，其核心是“對應”，并非“變化”.這一概念中，雖然十分注重“在某一過程中，存在兩個變量x與y”，然而概念的重點卻是“對于x的每一個確定的值，y都有唯一確定的值與它對應”.如果抓不住“函數”的核心，沒有理解，學生頭腦中的概念就是“y=關于x的式子”.為此，教師可以提供一些實際問題如腦電圖、統計表等，引導學生填表、列關系式等，認識問題中的變量、常量，歸納出這些問題中“兩個變量”所具有的共同特征，即兩個變量互相作用，當其中一個變量取一個確定的值，另一個變量有唯一確定的值和它對應.通過諸多對應關系的強化，學生對概念的核心才能正確地把握.

再比如，教學“隨機事件”這一概念，其核心是“結果不確定”，并非“不知道結果”.教師可以多舉實例，引導學生對其核心進行理解，如“火星上有沒有人”這句話不是“隨機事件”，原因是“結果不確定”——火星上“或者有人，或者沒有”，只是我“不知道結果”，沒有任何的隨機性，這是未知事件.如“判斷硬幣正面向上還是反面向上”這個問題，如果“在沒有擲以前”，這是隨機事件，因為“結果不確定”；如果“擲完了后蓋住讓其他人猜”，就不是隨機事件，要扣住核心“結果不確定”，不能因為非核心的因素“我不知道結果”而判斷失誤，其實“結果已確定”，只是“我不知道結果”而已.

2.突出“核心的概念”，讓學生構建認知結構

突出“核心的概念”，即在教學中，要正確把握和區分重要的概念和次要的概念，如果一節課中涉及的概念不只一個，教師不要平均用力，明確哪個概念是同化性概念，哪個是形成性概念，哪個概念對本節課有引領作用等，否則顧此失彼，對學生認知結構的構建有較大的影響.

同樣，在一章節中可能涉及多個概念，教師也必須確定概念在本章的地位，哪些概念有著“領袖”作用，分清主次，從而為確立教學重點打好基礎.在教學中突出這些核心的概念，提高學生分析與解決問題的能力.

如在學習《二元一次方程組》時，一位教師設置問題的方法很值得我們學習.

問題1：假如你手里有一根長為20 cm的鐵絲，將它首尾相接成一個正方形，這樣的正方形唯一確定嗎？（已知區）

問題2：若將它圍成一個長方形，這樣的長方形唯一嗎？（最近發展區）

問題3：若將長方形的長設為x，寬為y，是否滿足x+y= 10呢？這里的x、y的值唯一確定嗎？（用列表法解決問題）

問題4：上面正方形的長、寬是否滿足x+y=10呢？為什么卻能唯一確定呢？（在填表取值過程中，學生發現當x=y=5時，長方形轉化為正方形）

問題5：若在長方形的圍成過程中另外增加一個條件，那么這樣的長方形是否也能唯一確定呢？你能試添一個嗎？（解析方程組的概念，探索方程組的解的概念的形成過程）

問題6：如把20 cm長的鐵絲換成20根長為1 cm的木棒，將這20根木棒圍成長方形，這樣的長方形是否有無數個呢？

問題7：如果給問題6增加一個條件，比如2x-3y=5，這樣的長方形是否唯一確定呢？

教師通過設置一個個問題，一會兒把學生的思維逼到絕壁懸崖，讓它在絕處逢生；一會兒又把學生的思維一步步導向那廣闊的天空，讓它在高空中自由翱翔.這樣的課堂設問藝術，運用各種方式、技巧，學生自然會有“一番覺悟，一番長進”，既增長了知識，又開啟了智力，甚至有閃光的發現，獨到的體驗，該節課的核心知識也在不知不覺中得到了突破.

3.凸顯“核心思想方法”，讓學生提升解決問題能力

數學思想方法很重要.荷蘭數學教育家弗賴登塔爾研究認為：“數學中最重要的成份是思想方法.”《義務教育數學課程標準》也明確指出：“數學為其他科學提供了語言、思想和方法，是一切重大技術的基礎”.“通過數學教育，使學生獲得基本的數學思想方法……”這些都表明數學思想方法在教學中的重要性.學生掌握了數學思想方法，對理解和掌握相關的數學概念、知識大有幫助，因為二者屬于上下位關系，前者發生上位，后者屬于下位，當學生掌握和理解了數學思想方法后，再去學習相關的數學知識，具有較強的穩定性.

初中數學思想方法較多，其核心的思想方法如：從特殊到一般思想（如數與式中的運算律等）；數學建模思想（如把現實問題抽象為數學問題，利用方程或不等式等解決）；數形結合思想（如借助數軸解決有理數概念與運算律等）；化歸、函數思想（如解方程、方程組）等.教學過程中，教師要引導學生自主發現、理解這些從實踐中總結的數學思想方法.

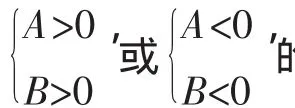
所以，在數學教學尤其是概念教學，凸顯核心的思想方法相當重要.說一節數學課“新”，即思維過程新，說一節數學課“高”，即思想性高.具有思想方法的課，學生對知識理解得更深更透，即使今后具體的數學知識淡化了，但其思考方法將永記心間.所以，教師應精心設計每節課，通過各種有效方式，為學生打開凝結在數學知識上的思想方法的閘門.

總之，數學教學中，應不斷強化數學核心概念教學，引導學生從概念出發，積極思考，并從中探討數學思想方法.在教學中避免出現忽視核心概念教學、避免出現遠離概念的核心教學，避免出現無視數學思想方法的教學，這些對于學生的成長是極為不利的.為此，應引導學生注重學習的過程性，將蘊含在數學概念中的思想方法挖掘出來，并漸漸體會與感悟，達到學以致用.