揭示本質 挖掘思想 注重思維 提升素養——例談蘇科版數學七下《平面圖形的認識（二）》復習設計

☉江蘇省連云港市新海實驗中學東校區 姜曉剛

揭示本質 挖掘思想 注重思維 提升素養
——例談蘇科版數學七下《平面圖形的認識（二）》復習設計

☉江蘇省連云港市新海實驗中學東校區 姜曉剛

數學復習是一種特殊的教學形式，在整個學習活動中是一個十分重要的環節，其基本任務是：在教師的引導下，幫助學生系統地復習、梳理已經學過的基礎知識，整合知識要點，構建知識網絡，總結解題規律，熟練基本技能，掌握思想方法，提升數學素養，使認知結構得到完善，思維能力得到發展.怎樣科學、合理地設計教學內容、精心地組織課堂教學呢？本文擬以蘇科版數學七下《平面圖形的認識（二）》進行例說.

日前，學校組織教學檢查，聽了七年級的幾節數學課，課題都是第七章《平面圖形的認識（二）》復習，幾乎都是按照以下的程序進行：

（1）提前下發復習學案，學生提前預習和試做（一份復習學案8K紙正反面，大致分為平行線的性質、平行線的判定、平移、三角形的概念、三角形的內外角和等幾個部分，每個部分又大致分為知識重現（填空）、經典例題（一道解答題）、針對性訓練（填空、選擇、解答）等欄目）；（2）上課時，分小組派代表陳述答案或展示某題的解題過程，生與師共同評點；（3）遇到集體性的問題或經典性問題，往往由教師主講；（4）最后由學生暢談本節課的收獲來結束復習課（有兩節課沒有完成預定的教學任務，沒有進入到此環節）.

這樣進行數學復習的優點是極大地發揮了學生學習數學的主體性作用，較好地體現了學習小組的互幫互助的價值，較好地讓學生展示自我，提升數學學習的自信.但是這樣的復習課缺乏“數學味”，如同之前的新授課的教學，沒有體現數學復習課的內涵和特色.

筆者認為：復習不是知識的簡單再現或分類，不是例習題的再現和重溫，而是要對數學知識進行梳理，幫助學生對舊知識進行回顧、深化，引導學生深入挖掘知識的內在聯系，進行系統整理要牽線成網，要充分發揮以題帶知識的作用，進而實現知識的遷移、綜合運用，以期實現數學復習課“揭示本質、挖掘思想、注重思維、提升素養”的主旨.

筆者結合自己的教學認識來談談本節課的教學設計.

一、進行知識梳理

數學知識之間彼此都是相互聯系的，在平時數學中，每課的知識點幾乎是孤立的，故在單元復習時應注意引導學生從單元的整體出發，按各知識點的內在邏輯關系進行比較、歸類、概括、抽象，將分散零碎的知識系統起來，形成清晰、完整的知識結構，由點連成線，由線織成網，能讓學生形成良好的認識結構，鞏固所學知識.

預習任務：

1.本章學習了哪些重要的知識和內容，你能用自己喜歡的方式梳理一下嗎？試試看！

2.在本章學習的過程中，你學會了哪些數學思想方法？能通過具體的實例說明嗎？與同伴交流吧！

設計意圖：布魯納指出：“知識結構的理解，能使學生從中提高他直覺處理問題的效果”.提前布置預習任務，讓學生用自己喜歡的方式梳理知識結構.上課伊始，可選擇部分學生的作品加以展示，并有目的地組織交流、組建結構，教師再給予及時的評價指導，這樣既有利于對知識的理解，又可讓學生體驗成功、增強自信.當然在教學過程中教師也可對單元的知識進行歸納整理，作為示范，潛移默化地影響學生學會組建知識結構.

如果學生暫時不具備單獨進行梳理的能力，也可提供如下的知識結構圖，讓學生學習理解和模仿.

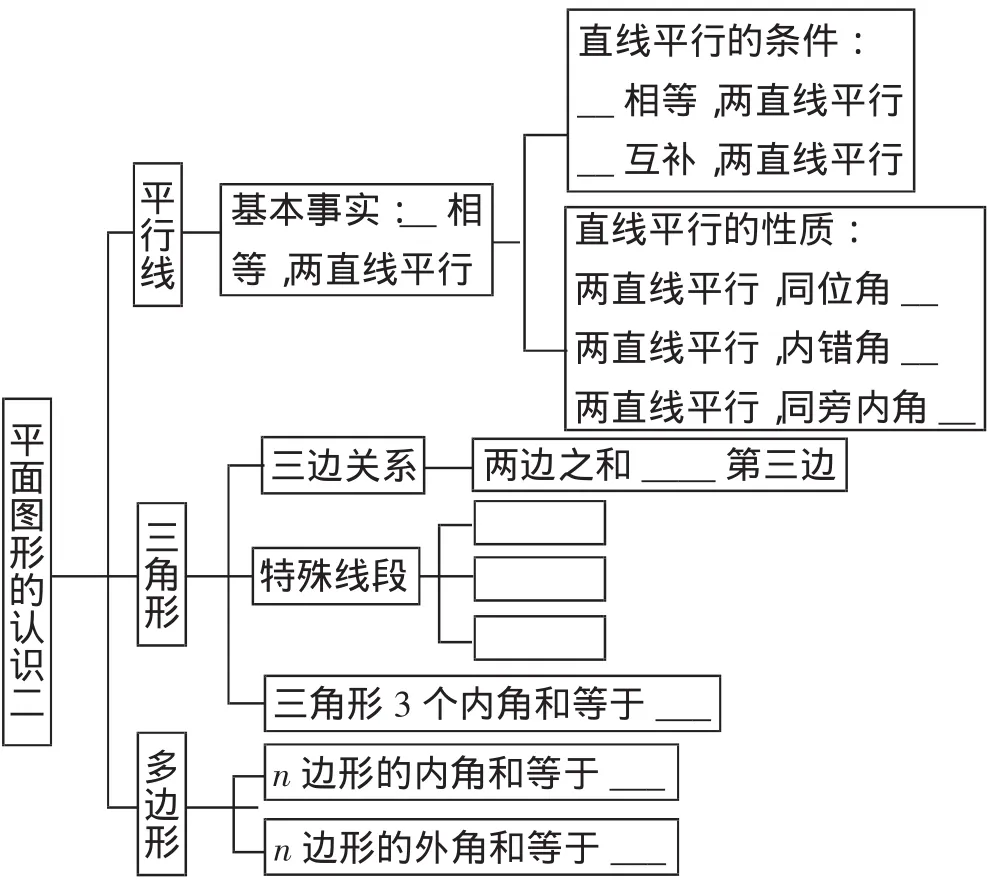
二、著重變式訓練

變式訓練就是對數學中的命題、例題、習題進行不同角度、不同層次、不同情形、不同背景的變式，從而暴露問題的本質特征，揭示不同知識點之間的內在聯系的一種教學方法.通過變式例題、習題教學，可達到一題多用、一題多解、一法多用、多題歸一的效果，從而提高學生學習的積極性，拓寬學生的思維空間.

變式訓練是數學復習課揭示本質、挖掘思想、注重思維、提升素養的一種有效的方式和途徑.

進行完知識梳理后，可出示以下例題并作系列變式.

例題 如圖1，在△ABC中，∠A=60°，BP、CP分別平分∠ABC和∠ACB，求∠P的度數.

如果將條件“∠A=60°”改為“∠A=α”，則∠P的度數如何表示？

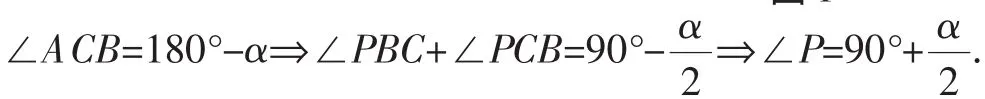
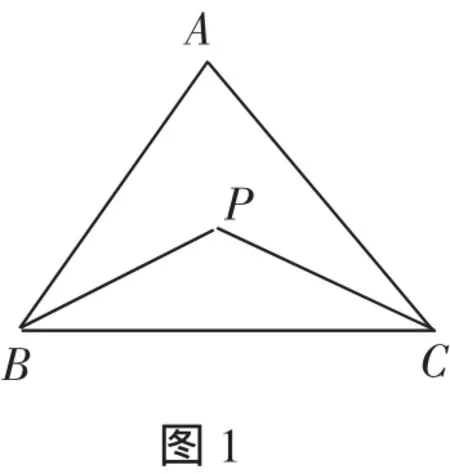
設計意圖：通過∠A求∠P，主要涉及三角形內角和定理，起點較低，難度不大，由數字到字母，體現了解法的一般性和結論的一般性.該題為學困生準備，也是下面系列變式和拓展的起點.

變式一：如圖2，在△ABC中，∠A=60°，BP、CP分別平分∠DBC和∠ECB，求∠P的度數.

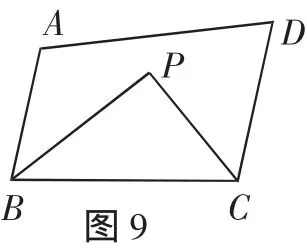
至此，問題得以順利解決，從中也體會到由“例題”一路進行變式（從內角平分線到外角平分線、從角平分線到角的三等分線、從三角形到四邊形）的價值，洞悉了圖形變化的本質，凸顯了解題的規律和思想.所以在復習教學中，例題的講解不能就題論題，要增加變式和解題反思環節，引導學生發現問題的本質，學會觸類旁通、舉一反三，內化其解題思想和方法，提高解決問題的能力和靈活應變的能力，提升學生的數學素養，從而實現有效復習和高效復習.

著名數學家波利亞說過：“一個專心的認真備課的教師能夠拿出一個有意義的但又不太復雜的題目，去幫助學生挖掘問題的各個方面，使得通過這道題，就好像通過一道門戶，把學生引入一個完整的理論領域.”這其實與我們常用的變式教學是一脈相承的.

數學復習課擔負著“知識結構的組織”和“數學知識的應用、數學思想方法的提煉”的雙重任務.前者是為了建構知識之間的關系，后者是為了鞏固知識，培養應用知識和解決問題的能力，發展數學思維.因此，在建構知識和查漏補缺之后，應該強化數學知識的應用和數學思想方法的提煉，選擇具有典型性、層次性和綜合性的問題，以題目代知識，以知識點歸類題型，以題型挖掘解題規律和數學思想方法，真正引導學生學會學習.

三、巧設數學活動

荷蘭教育家弗賴登塔爾曾說：“學習數學唯一正確的方法是實行再創造，也就是由學生本人把要學的東西自己去發現或創造出來；教師的任務是引導和幫助學生去進行這種再創造的工作，而不是把現成的知識灌輸給學生.”

《全日制義務教育數學課程標準（實驗稿）》明確提出：“數學要讓學生在參與特定的數學活動和具體情境中，初步認識對象的特征，獲得一些體驗.因此在數學復習中，如果能設置一些數學活動，讓學生在活動中發現問題、思考問題，嘗試運用已有的知識解決問題，既能提高學生學習的興趣，又能起到復習鞏固和提高的作用，何樂而不為呢！

在《平面圖形的認識（二）》復習時，可設置如下的數學活動.

數學活動1：給你一張長方形紙片，任意折出一條折痕，請再折出一條折痕，使它與前一條折痕平行，并解釋其中的數學道理.

設計意圖：學生可能會給出這樣三種折法：

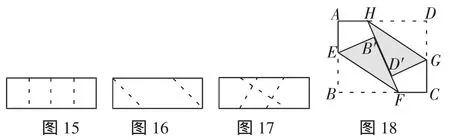
第一種：連續對折兩次后展開（如圖15），三條折痕均平行，理由是同位角（都是90°）相等或同旁內角（都是90°）互補，兩直線平行；第二種：將兩條短邊分別翻折到長邊上（如圖16），所得折痕平行，理由是同位角（都是45°）相等，兩直線平行；第三種：通過折任一條折痕的兩條垂線（七上知識，如圖17），從而這兩條垂線（折痕）平行.

這三種折法，學生能夠想到，也能說出理由.老師可以出示如圖18所示的折法（如有學生想到則更好），讓學生判斷并說理（其中涉及平行線的性質和判定）.通過折紙活動，既積累學生的基本活動經驗，又培養學生運用已有的知識解決問題的能力.

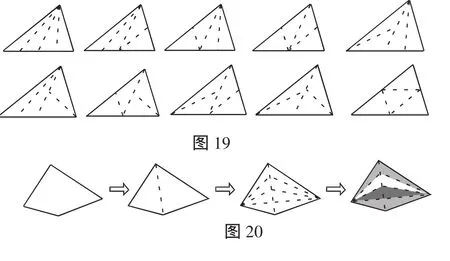
數學活動2：（1）給你一張三角形紙片，能否通過折紙的方法將它分成面積相等的四個部分？若能，請說明其中的數學道理.

（2）給你一張四邊形紙片，能否通過折紙的方法將它分成面積相等的四個部分？若能，請說明其中的數學道理.

設計意圖：活動2（1）主要是讓學生從解決問題的各種結果（如圖19）中感悟到三角形的中線具有平分三角形面積的性質.如果活動到此為止，那數學價值就大打折扣了，所以緊接著活動2（2），類似提出一個分四邊形面積為四個相等部分的問題，試圖讓學生通過轉化的數學思想，將四等分四邊形面積的問題轉化為四等分三角形面積的問題（如圖20），可凸顯數學思想的價值和作用，也為學生日后解決類似的問題提供了思考的策略和方法.

數學活動3：（1）給你一張三角形紙片（事先設定好三個內角分別為50°、60°和70°），請你任選一個角，按照圖21所示的方式折疊（使被折角的頂點落在三角形的內部），產生了∠1和∠2，再度量這兩個角和所折角的度數，并計算∠1+∠2.操作后與同伴交流結果，你有什么發現？能用所學的數學知識解釋嗎？

（2）如果將上述的三角形紙片按照圖22所示的方式折疊，產生六個角，這六個角的和是多少？你是如何得到這個結果的？

（3）取一張四邊形紙片，按照如圖23所示的方式折疊，產生八個角，這八個角的和是多少？你是如何得到這個結果的？

思考：如果是一張一百邊形的紙片，進行類似地折疊，將會產生200個角，那么這200個角的和會是多少？說說你的想法.

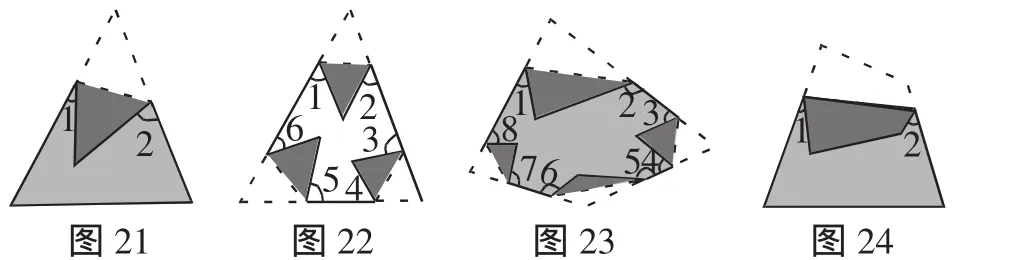
設計意圖：活動3（1）通過學生的操作和交流，發現∠1+∠2等于被折角的2倍，進而引發數學思考，嘗試運用已有的知識（途徑一：由鄰補角、三角形的內角和直接計算；途徑二：連接被折角的前后位置的兩個頂點，運用外角等于兩個不相鄰的內角和計算）解決，實現由合情推理到演繹推理的過渡.活動3（2）、活動3（3）既可以直接度量操作可得結果，也可運用活動3（1）的結論計算得到結果.當然選擇的不同，彰顯了思維層次上的差異.活動3（3）的思考，則是將提升了思維的深度和力度，因為尋求測量操作已行不通，只能通過數學縝密的說理和計算來獲得結果，從而揭示這類題組的本質.故數學活動是載體，經歷操作、發現和思考，滲透的是數學思想，提升的是思維品質.

如有可能，還可以出示圖24，讓學生繼續探究∠1+∠2與被折的兩個角存在著某種數量關系嗎？甚至繼續探究圖20中的頂點折至三角形的外部時，∠1、∠2與被折角存在著某種數量關系嗎？

綜上，如果數學復習課能恰當地進行知識梳理、著重變式訓練、巧設數學活動，可凸顯數學復習內涵和特色，以期揭示本質、挖掘思想、注重思維、提升素養.

1.中華人民共和國教育部制定.義務教育數學課程標準（2011年版）［M］.北京：北京師范大學出版社，2012.

2.姜曉剛.基于數學實驗的幾何復習課的設計［J］.中學數學（下），2013（9）.

3.姜曉剛.初中數學實驗教學設計的研究與實踐［J］.中學數學雜志（初中版），2013（10）.FH