推陳出新 適度暗示 能力突出解法多樣 教學引領——2013年中考成都卷第25題亮點分析

☉四川省四川大學附屬中學 劉成龍 張勤玲 楊巧華

推陳出新 適度暗示 能力突出解法多樣 教學引領
——2013年中考成都卷第25題亮點分析

一、試題回放

☉四川省四川大學附屬中學 劉成龍 張勤玲 楊巧華

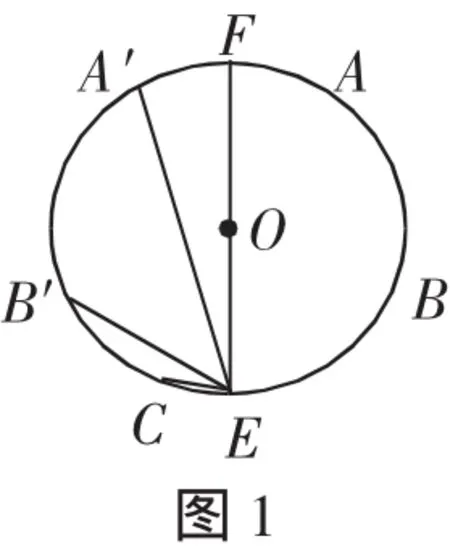
試題 （2013年中考成都卷第25題）如圖1，A、B、C為⊙O上相鄰的三個n等分點，AB=BC，點E在弧BC上，EF為⊙O的直徑，將⊙O沿EF折疊，使點A與A′重合，連接EB′、EC、EA′.設EB′=b，EC=c，EA′=p.現探究b、c、p三者的數量關系：發現當n=3時，p=b+c.請繼續探究b、c、p三者的數量關系：當n=4時，p=_______________；當n=12時，p=____________.

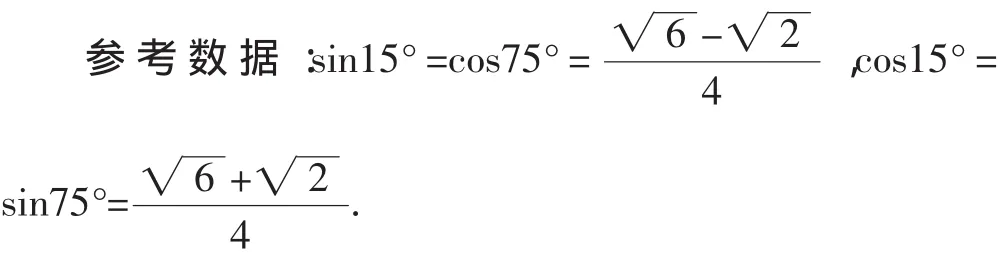
二、亮點分析

亮點1：推陳出新

命題者將正多邊形（正三角形、正方形、正12邊形乃至正n邊形）這一熟悉情景以圓周上的等分點形式展示給學生一個全新、公平的問題.直接以圓周上的等分點為背景的試題在中考試卷、模擬試卷和復習資料中幾乎沒有涉及，學生缺少應對的經驗，這使得試題情景新穎，具有一定的創新性，起到了推陳出新的效果.平常的“模式化引領”和“模式化訓練”使大多數考生面對試題時，因“始料不及”而“茫然”，這無疑是對“記題型，背套路，重解題方法，輕數學本質”的應試教育觀念的一次嚴峻挑戰.

亮點2：適度暗示

命題者在試題命制中，適度設置暗示，既不失壓軸題應有的區分度，又體現了對考生的關懷.

暗示1：命題者通過直徑EF引出了圓周上A、B、C的對稱點A′、B′、C′，以及EB′=b、EC=c、EA′=p，使得試題敘述冗長，不簡潔（事實上，試題可以簡潔敘述為：“A、B、C為⊙O上相鄰的三個n等分點，AB=BC，點E在弧BC上，連接EB、EC、EA.設EB=b，EC=c，EA=p”）.筆者猜測這是命題者故意而為之，目的是適度暗示：①暗示考生解答時可以從直徑所對的圓周角為90°考慮；②暗示考生解答時可以從對稱點的角度尋找解答思路.

暗示2：“現探究b、c、p三者的數量關系：發現當n=3時，p=b+c”這一句話可以從兩個角度解讀：①解答問題的起點是n=3，要先探究n=3時的情形；②p=b+c展示的是一條線段等于兩條線段的和，于是在方法上暗示考生考慮用截長、補短法.

暗示3：命題者在參考數據中給出了15°角的正、余弦值，考生可以這樣思考：15°角剛好是n=12時相鄰兩個點間弧所對的圓周角，給出其三角函數值，表明p、b、c與其三角函數值有一定關聯，自然暗示n=3、n=4時相鄰兩個點間弧分別所對的圓周角60°、45°的三角函數值與p、b、c相關.

亮點3：突出能力

“能力立意”是近年成都中考B卷壓軸題的命題原則.該試題展示了一個全新的問題，具有較大的思維空間，體現了主動探究的精神，呈現出研究性學習的特點，突出了對多種能力的考查，有效地甄別了學生的潛質.

（1）猜想的能力.

猜想是發現、獲取知識的重要方法，也是探索問題解決方法的重要手段.正如牛頓所說：“沒有大膽的猜想，就沒有偉大的發現”.該試題給我們的第一感覺是一道找規律題，整個試題充滿著猜想的味道，而破解該題的關鍵源于大膽的猜想.

（2）探究的能力.

“標準”指出數學探究指學生圍繞某個數學問題，自主探究、學習的過程.華羅庚教授說：“復雜的問題要善于‘退’，足夠地‘退’，退到最原始而不失重要性的地方.”該試題呈現探究性學習的特點，解答時先退回到問題解決的邏輯起點：n=3時，p=b+c.怎樣得到p=b+c的呢？怎樣用n=3的解決方案解決n=4、n=12呢？這涉及數學探究，基本的手段是“特殊到一般”，具體方法有以下幾種.

方法1：最直接的辦法——度量.

度量往往是探究的最直接手段.標準作圖，用刻度尺量線段的長度，然后猜測p、b、c間的關系，具體是：n=3時，取E為弧BC的中點，于是A與F重合，此時容易得出p= b+c.有了此經驗后，對于n=4，取E為弧BC的中點，EF⊥BC，度量線段長度，在誤差忽略的情形下結合45°角，可以大致猜出p=b+c.至于n=12，此法失效.

方法2：在度量的基礎上改進一下——計算.

基于方法1中的圖形，可知：當n=3時，b=c=r，EF=p=2r，可得p=b+c；當n=4時，b=c，通過計算得p=b+b，聯想到n=3時p、b、c的形式，可猜測p=b+c，當然這僅僅是一種猜測，有冒險的成分，需要驗證，但從某種意義上講為證明提供了方向.

方法3：在計算的基礎上提升——證明.

證明中運用的方法是截長、補短法.怎么截、怎么補是探究過程中首先要搞清的問題，這需要逐步試探調整（先探究n=3時的情形）.

截長法：

探究1 在EA上截取EM=c，再證明AM=EB=b.

探究2（探究1的變體）在A′E上截取EM=b，再證明A′M=EB=b.

探究3（探究1、2的升華）過C作CN∥EB，與AE相交于M，與⊙O交于點N，易得EM=c，再證明AM=EB=b.

探究4（探究3的變體）在弧BA上截取B（N=E（C，易得CN∥EB，回到探究3.

補短法：

探究5 在CE的延長線上取點M，使得EM=b，再證明EM=EB.

探究6 在EB的延長線上取點M，使得BM=c，再證明EC=BM.

（3）類比的能力.

“類比是一個偉大的引路人”（數學家G.波利亞語）.該題充分考查學生的類比能力：①解題思路的類比：截長、補短法類比、遷移到試題中；②操作方法（數學學習中積累的經驗）的類比、遷移：直接截長、平行線截長、直接補短等類比、遷移到該題；③類比n=3的解答方法解決n=4、n=12的情形.

亮點4：解法多樣

該試題情景看似陌生，但解法上具有很強的靈活性和多樣性，學生們可以從不同的角度審視，可以運用不同的數學知識和方法加以解答，真可謂異彩紛呈，這無疑為考生提供了展示才華和能力的機會.本題解答的常見方法有近10種，本質上都是截長、補短，下面列舉兩種解法與大家共享.

亮點5：教學引領

本題情景新穎，解答方法不偏不怪，是成都卷中的一道亮題.然而讓人驚訝的是，據閱卷信息透露，成都市中心城區近4萬名考生，得滿分（4分）的考生僅100人左右，問題究竟出在哪里呢？

從初三數學復習教學來看，課堂教學的主要任務是范例的講解與大量題目的演練，教師比較重視學生對數學基礎知識的記憶，忽略學生對數學本質的理解；重視學生對題型、套路與解題方法的訓練，忽略學生對思想、方法的總結提煉；重視學生對具體問題的解決，忽略學生對開放性問題的處理，尤其缺乏對創新意識的培養.

從學生的學習方式來看，初三數學課堂復習的基本模式是“教師講—學生聽—學生記”、“教師示范例題—學生模仿練習—學生記憶基本題型”，這是一種“單向”信息傳遞的教學模式，學生處于被動接受的狀態，屬于“簡單模仿—低能操作”式學習，只能在數量上增加學生數學認知結構中的某些信息，不利于知識和方法的主動構建.

三、教學啟示

1.改進教學方式

“標準（2011年版）”倡導“積極思考、合作交流、動手實踐、自主探索的學習方式”.因此，初三復習中，教師應讓單向信息傳遞的教學模式“動”起來.首先是行動起來.教師應精心設計教學內容、呈現形式、講解方式，激發學生持續學習的熱情和欲望，引發他們的行為參與、認知參與與情感參與，使學生能夠全身心投入到初三復習中來.其次是互動起來.教師要重視師生之間的相互合作、相互溝通，充分發揮學生的主體地位，還課堂于學生、還時間于學生、還話語權于學生，引導學生之間充分交流，從而在師生對話、生生對話的過程中，達成“互識”和“共識”.再次是思維靈動起來.數學是思維的體操.數學的學習過程是學習者情感、態度、信念、價值的賦予過程，更是思維的萌芽、成長和成熟的過程.在經歷問題的提出、分析、解答過程中，培養學生思維的多樣性、批判性和靈動性.

2.加強創新意識的培養

本題具有形式新、背景新等特點，屬于創新型試題.此類試題不是問題的簡單呈現，“刺激—反應”的解題套路無法奏效，一般來說解答需要經歷以下過程：閱讀新信息—加工新信息—得到問題的本質—獲得問題的解.這一過程需要學生具備閱讀能力、信息捕捉能力、自主學習能力、探究能力、創新意識等.從閱卷信息來看，學生缺乏應對新問題、新情景的能力.因此，教學中應加強培養學生的創新意識.

1.趙思林，潘超.一道以群的定義為背景的高考試題賞析［J］.中學數學（上），2008（4）.

2.劉成龍.由一個物理問題引起的探究性學習［J］.中學數學教學參考（中），2013（7）.

·江蘇省無錫市龐彥福名師工作室·