解答數學題是干啥的？

☉江蘇省睢寧高級中學南校 吳少堂 黃安成

解答數學題是干啥的？

☉江蘇省睢寧高級中學南校 吳少堂 黃安成

我們都知道解答數學題是鞏固知識、熟練技能、訓練思維、發展智能、優化心理和磨礪意志的需要，歸根到底是為了提高考試成績、升入理想的大學.但本文從另一個視角來解讀，則得到意料之外且新穎別致的答案，但究其實質，卻又在情理之中.

一、解答數學題是游戲玩耍

將解答數學題的活動變為游戲玩耍，這是多么神奇美妙的一種境界！世界級的數學大師陳省身先生最著名的話語就是“數學好玩！”由此，解數學題就不再是一種“痛苦的折磨”，而是一種愉快的享受！當然與打籃球、下象棋一樣，這種“玩”有時也不是一件十分輕松和順利的事情，但由于“玩心太重”，困難與挫折也就不在話下了.

例1 求sin238°+sin282°-sin38°sin82°的值.

解析“：38°、82°”，何方“怪物”？何怪之有？38°+82°= 120°，那么38°、82°、60°就是一個三角形的三個內角，則可取△ABC，使∠A=38°，∠B=82°，則∠C=60°.由此想到余弦定理a2+b2-2abcosC=c2，再由正弦定理得4R2sin2A+ 4R2sin2B-2×4R2sinAsinB°cosC=4R2sin2C°，則得sin2A+ sin2B-2sinAsinB°cosC=sin2C.

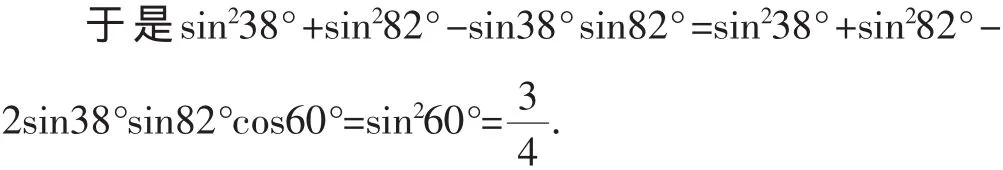
兩個重要定理引領字母a、b、c與A、B、C以及一些數字做游戲，玩得可真算是智趣盎然、豐富多彩！

例2 已知a=（cosα，sinα），b=（cosβ，sinβ），0<β<α<π.

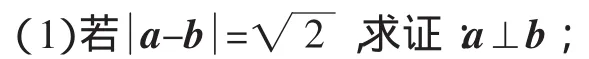
（2）設c=（0，1），若a+b=c，求α、β的值.

解析：字母、數字和運算都是我們的“玩具”，此外各種圖形也是我們的“玩具”啊！此題是2013年某省的一道高考題，下面給出一種與公布的答案大相徑庭且別開生面的解法.

（1）由已知得表示向量a與b的點A與B都在單位圓上（如圖1）.

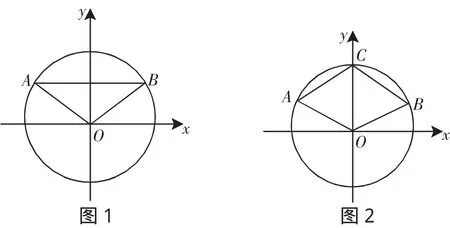
（2）又因為c=（0，1），表示單位圓上的點C（如圖2）.

又a+b=c，所以AOBC構成∠A=60°的菱形，∠xOA= 150°，∠xOB=30°.

沒用任何計算，兩個非常熟悉的平面圖形成了我們得心應手的“玩具”，想玩，會玩，運用與向量有關的“游戲規則”，可謂玩得絢麗多姿、賞心悅目.

二、解答數學題是刑偵破案

刑偵破案講究四點，第一，獲取的破案線索和有關信息很可能少得可憐，須擴大搜尋的范圍；第二，獲取的破案線索和有關信息雖然不少，但須經過精心辨析和篩選，去粗取精，去偽存真；第三，不可能一下子鎖定作案人，開始時很可能只是懷疑對象，且懷疑的范圍可能比較大，必須逐步縮小這個范圍；第四，范圍先擴大，后再縮小，當獲取的線索和有關信息形成有力的證據鏈時，最終鎖定犯罪嫌疑人，辦成無懈可擊的鐵案.需要的是理性思維和悟性思維的密切配合.

現在的任務就是通過穿云破霧、抽絲剝繭，以確鑿的證據鎖定“嫌疑人”，以便將它“捉拿歸案”.

首先由③得a5q+a5q2=3，結合②得q2+q-6=0.此關于q的方程有兩個根，結合①知q=2.

因為n∈N+，所以1＜n≤12，所以n的最大值為12.

辦案刑警為保一方平安，經常不辭勞苦、廢寢忘食，甚至不顧生死地連續作戰，大功告成后才倍感幸福.在這里我們當與他們感同身受了.

三、解答數學題是魔術揭秘

某些數學題的結構以及結論常顯得匪夷所思和離奇古怪，真有些“魔幻”色彩.舞臺上，魔術師的表演是不會將其中的奧秘告知觀眾的，故魔術表演被稱為“掩蓋真相的藝術”.揭露真相會使魔術失去懸疑性和觀賞價值.可是數學題的解答與此卻正相反，是完全徹底的“魔術揭秘”.

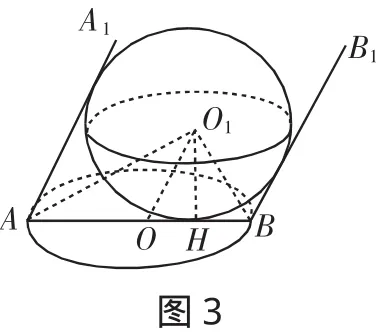
例4 水平地面上有一個籃球，它與地面唯一的接觸點（即球與地平面的切點）為H（如圖3），在斜平行光線的照射下，其陰影為一個橢圓.求證：H是橢圓的一個焦點.

解析：經斜平行光線的照射，球在地面上的陰影是橢圓形，很容易理解.可匪夷所思的是，這里的點H竟然是橢圓的一個焦點.這是命題者令人感嘆的發現.發現也是一種創造嘛！我們能揭露其中的奧秘嗎？

設球心為O（1作輔助線過程略），設橢圓的長半軸、短半軸、半焦距的長分別為a、b、c，球的半徑為R，設橢圓的中心為O，那么在Rt△AO1B中，OA=OB=OO1=a，則要證的是OH=c.

戳穿謎底，原來如此簡單.可魔術師堅守秘密是行規，數學教師揭示秘密也是行規啊！

解析：告訴你們，也許你們不信，已知函數式竟能化為cosθ-sinθ，“毛毛蟲”蛻變為“花蝴蝶”，是什么“魔法”使然？現在就來揭穿其中的奧秘.

可能會有人質疑，這種“戲法”也太特殊了，能算通法嗎？三角代換法算不算通法？算.凡變量a2+b2=1，則都可以設a=cosθ，b=sinθ；凡變量t∈［-1，1］，則都可以根據需要設t=cosθ，或t=sinθ；凡t∈R，則都可以設t=tanθ.不過這里有點小變化，設的是x+1=tanθ，為什么？圖方便嘛！看似特技，實為通法.揭穿謎底，決不可怕！

四、解答數學題是觀賞景致

數學是充滿美的科學，我們則要努力既是景致的創造者，又是景致的觀賞者，觀賞自己辛勤加智慧的勞動成果，心理更加踏實和幸福.許多數學題目的多種解法，就給人以瑰麗多姿、流光溢彩的心理感受.特別地，當多種解法各具特色、風格迥然時，則除了觀賞價值外，還具有“方寸天地，氣象萬千.一舉多得，收獲一片”的功效.

例6 △ABC的內角A、B、C所對的邊a，b，c成等差數列，且A-C=90°.

解析：題目的已知條件非常“樸素”、“貌不驚人”：a，b，c成等差數列，且A-C=90°！可是欲證的結論卻奇特異常，竟與無理數“”發生“親緣”關系，想破腦袋也不會想到這樣的結果！但此結論不僅不容置疑，且我們發現了六種不同的思路，限于篇幅和時間，這里僅給出其中的四種.

思路1：由已知，必有a＞b＞c，則可設a=b+d，c=b-d（0＜d＜b）.

最容易想到的就是此思路，不過計算比較麻煩些.但若掌握有關技巧則可減少麻煩.如將cosC的表達式中的“d”換成“-d”就得cosA的表達式；在得到關于d的方程后，在動手解題之前就可判斷此方程必有解d=■ 7b，則給這個四次方程的解答帶來很大的方便.

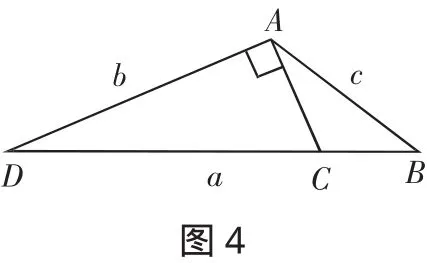
不須動筆，即知此方程必有解為d=1.豈不精妙至極！

有了三邊的關系，如何證得結論，這里就不贅了.

僅有四十幾個字符的短題，解起來竟涉及眾多知識、技能、技巧和思想方法，對豐富大腦營養的補給和思維的啟迪，收獲太豐碩了，且精湛景致的創造和欣賞在心靈中將留下美好而深刻的記憶.

五、解答數學題是科研探索

雖然中學生離真正意義上的科研探索還很遙遠，但我們在教學中可以且應該大力提倡探究式的學習方式，努力引領學生在問題解決中逐步學會運用數學探索的手段和方法，走進數學科研的門檻，初步品嘗數學科研的滋味，感受獲得成果的喜悅，啟發向科學進軍的決心和動力，為將來從事真正意義上的科研探索打下知識、技能、思維、心理和意志品質的基礎.

例7 在平面直角坐標系xOy中，若已知A（x1，y1）、B（x2，y2）、C（x3，y3），你能求出△ABC的面積S嗎？請將這個問題作為數學科研課題，寫出小論文.

三角形的三個頂點的坐標確定，其面積肯定確定，問題是如何建立面積S與六個字母之間的內在聯系.學生在以往解題時已獲得了初步經驗，即先從簡單的特殊情況入手，然后再將問題一般化，最后力爭將結論簡單化，既重視此結果，更享受其過程，并總結進行數學科研探索的心得與體會.

解析：先研究一種特殊情況，即C與原點O重合（如圖5）.

再研究一般的情況，盡可能應用上面已獲得的成果.

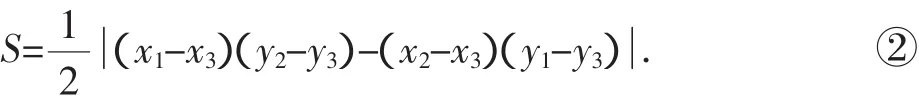
學生回顧科研探索的過程時，感慨萬千，他們表示：雖然這個結論也許早已存在，但對于我們來說卻是第一次接觸，所以仍具有研究的突破性（教者插話：你們今后將會取得更大的實質性的突破）；要不是先來個特殊化，這個問題根本就解決不了（教者插話：能解決，但麻煩太大了.先特殊后一般是數學研究，也幾乎是所有科學研究的規律）；當得到cosθ的表達式后，欲想求sinθ的表達式，心里開始也有過動搖，后來堅定了決心，才執著地堅持了下去，沒想到代入面積公式后，經過約簡，竟得到一個非常簡潔的公式①（教者插話：若不堅持，又怎能從奇妙的過程中享受到無比的樂趣.公式①簡單的顯示是數學的簡潔美，越簡單的結論，越有實用價值，越具有生命力.雖然公式②不算很簡單，但后來人們創造了一個數學工具，可以迅速記住并掌握這個公式，不過現在還不能告訴你們）；整個探索過程具有一定的創造性，但不能否認扎實的基礎知識和技能的重要作用（教者插話：夯實基礎與思維靈活兩者不可偏廢，且相得益彰）；此問題當然不可能成為高考試題，但具備了這種探索科研能力，以后在考場上遇到從未見過的試題，也能做到處變不驚、臨危不亂，最終實現克“題”制勝（教者插話：從現在起就打下探索科研的深厚扎實基礎，將受益終生）.

六、解答數學題是工程建筑

隨著國家建設的飛速發展和日新月異，各種工程建筑紛紛上馬.面對這些工程，我們常在想，解答數學題不也是在搞“工程建筑”嗎？特別是一些中、大型綜合題的解答，更需要經過“勘探、設計、施工、監督、完工、驗收”等基本程序，有時候還要進行“定期回訪”和“跟蹤服務”.工程中還有數不清的各種管道和線路，既需要整體的宏觀設計，又需要精心的細微加工.遇到關鍵“節點”，還要想方設法予以即時和恰當的處置.

例8 設函數（fx）=x4-2ax2，已知當x∈［0，1］時，關于x的不等式＞1的解集為空集，求滿足條件的實數a取值的集合.

解析：勘探：（fx）是四次函數，f（′x）是其導函數，求滿足條件“…”的實數a取值的集合.

由于x∈ ［0，1］，所以須由淺入深和由易到難地對x不同的值進行分類討論：

1°若x=0，①式成立；

除了以上所說，還可以說解題是登山采寶，解題是入海探秘，解題是破譯密碼，解題是戰場拼搏，解題是……但歸根結底還是本文開頭的回答.