自主訂正：知識“內化”的重要途徑*

☉江蘇省如皋市江安鎮濱江初級中學 周文斌

自主訂正：知識“內化”的重要途徑*

一、寫在前面

☉江蘇省如皋市江安鎮濱江初級中學 周文斌

在學生學習的各個階段，充斥著各種各樣的考試，很多考試都是為了對學生前一階段的學習狀況進行“摸底”.在這些考試中，學生出錯是不可避免的.這些錯誤的生成原因是多樣的，有些是學生的認知缺陷所致，有些是學生的解題“陋習”所致.適時講評可以彌補學生認知的缺陷，適量訓練可以矯正學生的解題“陋習”.但是，無論是知識的“補缺”，還是“陋習”的矯正，都必須通過學生的自主訂正來實現.自主訂正非常重要，它是學生知識“內化”的最重要的途徑.本文擬結合一次檢測講評課中的“自主訂正”的設計談談個人對此的感悟，以期對您有所幫助.

二、一次試卷講評課的“自主訂正”設計

（一）測試背景

本次測試安排在中考一輪復習之后，主要是對前一階段復習的一個總結與提升，同時通過“彌補缺陷”為下一階段的復習做好鋪墊.本次考試，考查了前一階段的一些基礎知識和基本技能，涉及初中數學的很多核心知識，當然一些常見的數學思想和活動經驗也滲透在試題之中.全卷共27大題（35小題），滿分150分，其中選擇題10題，填空題8題，解答題9題.在試題編排時，將選擇題、填空題的最后一題，解答題最后一題（主要是第3小問）設置為全卷的“壓軸點”，以此來控制滿分；選擇題、填空題余下的題目和解答題的前6題難度很低，學生解答較為容易，有部分考題甚至是“送分題”，學生基本不會出錯；解答題的后三題共26分，難度中等，有一定的區分度，中等學生基本能完成解答，但在解題中會出現失誤.

（二）“自主訂正”時的設計及分析

1.試卷講評前

教學設計：

請同學們將4～9，11～17，19～24，27（1）中出錯的題目自行訂正，將這些題目中用到的知識、方法及數學思想梳理一下，寫在題目的旁邊.這些題目中沒有出現錯誤的同學，訂正自己出錯的其他題目.

部分試題呈現：

第26題 如圖1，在Rt△ABC中，∠C=90°，BD平分∠ABC，DE⊥BD交AB于點E，⊙O是△BDE的外接圓，交BC于點F.

（1）求證：AC是⊙O的切線.

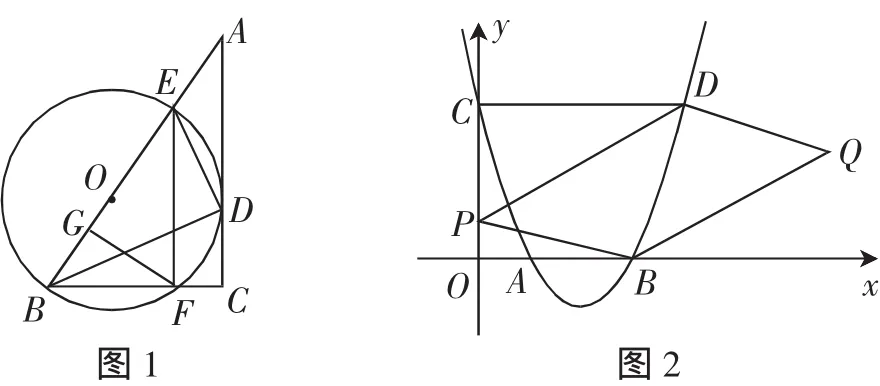
第27題 如圖2，已知二次函數y=x2+bx+c的圖像與x軸交于A，B兩點，交y軸于點C，過點C作CD⊥y軸交該拋物線于點D，且AB=2，CD=4.

（1）該拋物線的對稱軸為______________，B點坐標為____________，CO=___________.

設計意圖：在講評之前，選擇了三類題目讓學生自主訂正：第一類，計算錯誤的，如第19題，同學們都能用待定系數法列出方程組，但解方程組出現了計算錯誤；第二類，讀題不清，如少數同學解答第22題時沒有求出整數解，解答第27題第（1）題時沒能將數與形進行簡單的結合；第三類，個案錯誤，如第4題只有兩個同學出錯，第26題第（1）問有6位同學出現問題.這些試題，難度較低，解答出錯的學生不多.當給他們自己再度審視試題的機會時，他們一般都能給出正確的解題過程.于是，筆者將這些題目拼在一起，讓學生能在短暫的時間內將解答中出現的“問題”化解，為接下來的小組交流和全班交流贏得時間.

2.小組交流后

教學設計：

先在學習小組中交流：10，18，25，27（2），理清本組同學解題中出現錯誤的原因，找到正確的解題方法，并將這些試題涉及的知識梳理一下，然后自主訂正.

在學生交流時，教師巡視課堂，并參與小組交流，對學生解題中出現的典型錯誤進行點評，對學生在小組內交流后仍然存在的“困惑”進行即時解答.

部分試題呈現：

第10題 如圖3，在正方形ABCD中，點E為BC邊的中點，點B′與點B關于AE對稱，B′B與AE交于點F，連接AB′，DB′，FC.下列結論：①AB′=AD；②△FCB′為等腰直角三角形；③∠ADB′=75°；④∠CB′D=135°.其中正確的是（ ）.

A.①② B.①②④ C.③④ D.①②③④

第27題 （2）若P為線段OC上的一個動點，四邊形PBQD是平行四邊形，連接PQ.試探究：

①是否存在這樣的點P，使得PQ2＝PB2＋PD2？若存在，求出此時點P的坐標；若不存在，請說明理由.

設計意圖：這些是中等難度試題，有一定的區分度.從試卷分析的情況來看，考試時只有部分學生給出了正確的解題過程，失分很多.通過對學生解答情況的詳實分析，筆者發現學生出現的這些錯誤，很多是因考試時思維的“暫時性短路”所致.這主要是由于學生知識網絡的建構不到位所致.因此，在教學中，我們可以通過小組交流來推動學生認知網絡的完善，讓學生在交流中實現知識的關聯與融合.基于此，筆者將這類考題列入“先小組交流，后自主訂正”之列，通過小組內的充分交流，有效梳理解答問題中的“共性錯誤”，分享全組成員的解題經驗，獲得正確的解題方法.在小組交流后，對這些題進行自主訂正，能將學生在小組交流中的收獲迅速“內化”，彌補認知的不足，促進知識網絡的完善.

3.全班交流后

教學設計：

通過師生互動對話，在全班交流27題第（2）問的第②小問，將解決這一題用到的知識、方法、數學思想進行徹底梳理，并對同學中出現的各種失誤進行了集中點評，交流正確的解題思路和解題方法.在此基礎上，要求學生自主訂正.

部分試題呈現：

第27題 （2）②當PQ長度最小時，求出此時點Q的坐標.

設計意圖：本題是全卷的壓軸題，難度較大，全班只有一個學生給出了正確的答案，大多數同學只給出了部分解題環節，有少數學生未對本題進行任何解答.對此題采用全班交流的形式，意在通過師生的互動對話，明晰本題的解題思路，梳理知識應用中的技巧，呈現涉及的數學思想.對這些方面的即時點撥，能讓學生深入感知本題的考試意圖，體驗到初中數學核心知識在解題中的“應用價值”，從而獲得問題解決的基本方法，歸納整理此類考題的通用解法，為接下來的自主訂正和再度應用做好鋪墊.

三、教學感悟

1.分段實施，強調過程體驗

無論是階段性考試，還是本文中所述的中考前的模擬考試，試題的編排都必須遵循學生的認知規律.一份試卷，試題的分布應符合“教學常態”，難易題的分布要合理，既要有多數學生能夠解答的“基礎題”，也要有只有少部分學生能夠解決的“壓軸題”.就算是同一道考題，不同分支也因承載著不同知識的考查任務，而使其難度不盡相同.事實上，“多問”考題一般梯度都很明顯，難易度非常清晰，小題之間具有明顯“關聯”，難度隨著題號不斷增加.因此，在安排學生自主訂正時，教師應根據試題的難易程度和學生的解答狀況對試題進行組合，根據不同的教學進程，實施分段訂正.通過分段訂正的實施，讓學生充分體驗解題的過程，在自我的主觀感悟中，“品味”錯誤，找到正確的解題路徑，實現糾錯與提升的雙重教學成效.

2.重在點撥，提升內化成效

學生在考試中出現的解題錯誤，很多是在特定時段內解題思路不暢通所致.在經歷了知識學習和適量訓練后，解題出現短暫的知識融合困難是不可避免的.這些“困難”是暫時的，主要成因不是知識的不足，而是知識網絡建構不到位.因此，在自主訂正前，我們可以通過學習小組或全班交流，在師生互動、生生互動中對解題思路進行必要的點撥，幫助他們將已有知識與試題情境進行關聯，從而點破他們考試時的困惑，為他們“指點迷津”，讓他們“豁然開朗”，進而帶著愉悅與興奮的心情將交流的成果轉化為訂正的成果.這些適時的互動點撥，讓學生將解題中的犯錯經驗以及錯誤試題涉及的知識、技能、思想方法和經驗“內化”為自己的東西，為今后的解題提供可以借鑒的寶貴經驗.

3.分層落實，確保糾錯實效

讓每一名學生學有所獲，是每一節數學課的教學任務，試卷講評課也不例外.課前，在對“自主訂正”進行設計時，我們也應認真分析每一名學生的考情，讓他們在講評課上均有所獲.要特別注意的是，絕不能將所有學生都置于同一個能級上進行訂正設計.必要時，應該對學生或試題進行適度分層，讓每一位學生訂正自己能訂正的試題，從而解決“吃得了”與“吃得飽”的問題.這種設計理念，在上面的案例中有著明顯的體現.如對“講評前”的自主訂正提出了“這些題目中沒有出現錯誤的同學，訂正自己出錯的題目”的要求，這實際上解決了一部分優等生的“無事可做”的問題，讓他們在后進生自主訂正時段內，能思考自己的“問題”，提前進入自我反思和自我提升的階段.這樣的教學設計，為優等生積累了小組交流和全班交流的“素材”，讓他們能在交流中盡情發揮，以提高其認知的水平和解決問題的能力.

四、結束語

在考試中，學生出現錯誤是正常的.對教師來說，處理好學生出現的這些錯誤是試卷講評課的一個重要任務.通過這些錯誤實現學生認知的“查漏補缺”，應該是試卷講評的一個重要任務.那么，如何實現“補缺”的任務呢？筆者認為，自主訂正是一劑最為有效的“良藥”.通過對不同教學時段的“自主訂正”的巧妙設計與實施，每一名學生都能在自主訂正中做好“過錯”反思，化解“錯誤”，找到正確的解題方法.毋庸置疑，在訂正的過程中，學生的認知會隨著訂正的進程不斷攀升，知識技能、思想方法等都會得到大幅度的提升，這些對學生解決問題能力的提升都是十分有益的.

以上是筆者試卷講評課上“自主訂正”環節的一些做法和思考，不足之處，歡迎各位同行批評指正.

1.中華人民共和國教育部制定.義務教育數學課程標準（2011年版）［M］.北京：北京師范大學出版社，2012.

2.印冬建.淺談試卷講評必須抓住的幾個“要點”［J］.中學數學（下），2013（2）.FH

*本文為江蘇省南通市教育科學“十二五”規劃立項課題“農村初中小班化教學中復式分組的實踐與研究”（編號：NT2011361）的研究成果.課題主持人：印冬建，本文作者系該課題組成員.