走進拓展，竟如此美麗——記2013年江西中考幾何壓軸題的研究與拓展

☉江西省安福縣城關中學 曹經富

☉江 西 省 教 研 室 陳莉紅

走進拓展，竟如此美麗
——記2013年江西中考幾何壓軸題的研究與拓展

☉江西省安福縣城關中學 曹經富

☉江 西 省 教 研 室 陳莉紅

中考壓軸題或課題學習類試題，通常以學生熟悉、感興趣、有價值的素材或數學活動為切入點，立足于知識、問題的生長點、發展點、延伸點，借助操作活動、經驗、知識、思想方法等，培養感性直覺和理性思考為目標，重在考查考生發現問題、提出問題、分析問題和解決問題的能力.作為數學教師，在日常教學中，如果挑選一些具有廣闊前景的中考試題，進行適當的拓展與延伸，深入思考與探究，舉一反三，放棄題海戰術，以一當十，我們就能獲得最大限度的收獲.現以2013年江西中考幾何壓軸題為例進行拓展與延伸，與大家分享與探討.

例：（2013年江西）某數學活動小組在作三角形的拓展圖形，研究其性質時，經歷了如下過程.

●操作發現：

在等腰△ABC中，AB=AC，分別以AB和AC為斜邊，向△ABC的外側作等腰直角三角形，如圖1所示，其中DF⊥AB于點F，EG⊥AC于點G，M是BC的中點，連接MD和ME，則下列結論正確的是_________.（填序號即可）

●數學思考：

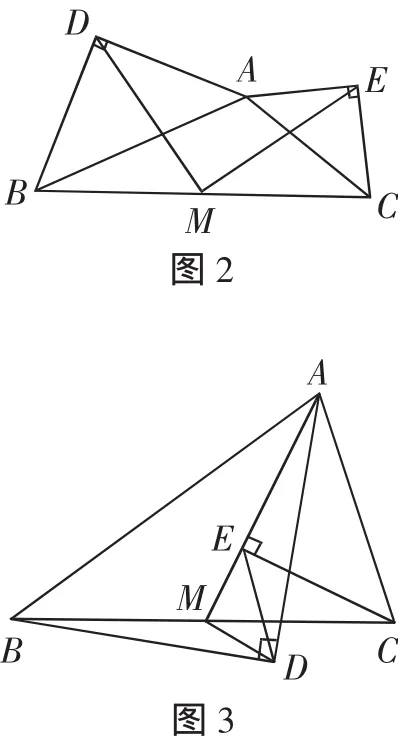
在任意△ABC中，分別以AB和AC為斜邊，向△ABC的外側作等腰直角三角形，如圖2所示，M是BC的中點，連接MD和ME，則MD和ME具有怎樣的數量和位置關系？請給出證明過程.

●類比探索：

在任意△ABC中，仍分別以AB和AC為斜邊，向△ABC的內側作等腰直角三角形，如圖3所示，M是BC的中點，連接MD和ME，試判斷△MED的形狀.

答：__________________.

解析：操作發現：①②③④.

數學思考：MD=ME，MD⊥ME.

類比探究：等腰直角三角形.

評析：本題以動態三角形為背景，以兩邊為斜邊向外構建等腰直角三角形，探究兩直角頂點與第三邊的中點所連線段之間的位置關系和數量關系，注重從特殊（圖1）到一般（圖2），即從特殊等腰三角形入手，逐步過渡到任意三角形，當從點A在BC的上方過渡到點A在BC的下方時（圖5）（也就是題中兩邊為斜邊向內作等腰直角三角形（圖3）），幾何屬性的結論仍保持不變，有助于引導教師和學生在日常的教學與學習中注意觀察與思考相關幾何圖形的變與不變的屬性.本題所考查的知識與能力相當豐富與深奧，如特殊三角形的性質（等腰三角形、直角三角形、等腰直角三角形）、三角形的中位線、平行四邊形的判定與性質、三角形全等的判定與性質、平行線的性質等，試題巧妙地設置“操作發現”、“數學思考”、“類比探究”由易到難的三個層次.在“操作發現”中，設置一些簡單的補充說明文字與判斷選項題，起點低，入口寬，讓學生作出分析與思考后直接進行判斷，循序漸進地引領學生在觀察操作中積累一定的數學活動經驗及簡單邏輯推理；在“數學思考”中，通過背景圖形的變化（從特殊等腰三角形，逐步過渡到任意三角形），將數學問題的特殊性拓展到一般性、普遍性，進行推廣與應用，由直覺感觀逐步上升到理性思考，要求學生運用所學知識進行分析、綜合、探究與求證；在“類比探究”中，進一步將問題推向一個新的高峰與推理.該幾何壓軸試題也飽含命題者的良苦用心及對廣大學生的人文關懷，如在“操作發現”中的特殊圖形的相關輔助線示范、補充與提示，由易到難的層次的設置，相關幾何圖形由特殊到一般的變化過程，幾何圖形性質的不變性等，都給了學生很好的啟示、引領與水到渠成的提示.

“橫看成嶺側成峰，遠近高低各不同”，在試題研究和課堂教學中，如果我們能以三角形、四邊形等基本圖形為背景，以相關邊長或某些線段的長作正多邊形，借助相關點動，帶動背景圖形（三角形、四邊形等）的變化，相關圖形之間的位置、形狀與大小關系卻依然保持著某些結論的變與不變的屬性，給我們增添無窮的趣味性、想象力和探究力.

拓展1：在任意△ABC中，F、G、M分別是AB、AC、BC的中點，分別以AF、AG為邊向外作正n邊形（n為大于2的整數），如：正三角形ADF，正三角形AGE（圖6）；正方形AFDL，正方形AGEO（圖7）；正五邊形AFDLO，正五邊形AGEXY（圖8）；……，∠EMD=y.

（1）探究MD和ME的大小關系；

（2）寫出y與n之間的關系；

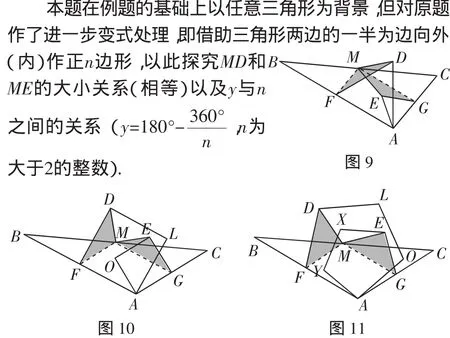
（3）當點A位于BC的下方時（即向內作正n邊形，如圖9、圖10、圖11），（1）和（2）中的結論是否依然成立？

拓展2：以四邊形ABCD的邊AB、AD為邊分別向外側作等邊三角形ABF和ADE，連接EB、FD，交點為G.

（1）當四邊形ABCD為正方形時（如圖12），EB和FD的數量關系是_________.

（2）當四邊形ABCD為矩形時（如圖13），EB和FD具有怎樣的數量關系？請加以證明.

（3）四邊形ABCD由正方形到矩形到一般平行四邊形的變化過程中，∠EGD是否發生變化？如果改變，請求出∠EGD的度數.

本題在例題中三角形的基礎上拓展：以動態特殊四邊形為背景，以一組鄰邊為邊向外作等邊三角形，醞釀與構建從特殊（正方形到矩形）到一般（平行四邊形），以此進一步類推，以這組鄰邊為邊向外作正n邊形，始終保持相關圖形之間位置、大小、形狀之間的變與不變的幾何屬性（線段之間的數量關系及所夾角度）.

拓展3：如圖17～19，以矩形ABCD的邊AB、AD為邊分別向內側作等邊三角形ABF和ADE，連接EB、FD，它們相交于點G或它們的延長線交于點G.∠EGD是否發生變化？并求出∠EGD的度數.

解析：以矩形ABCD的邊AB、AD為邊分別向內側作等邊三角形ABF和ADE.當點G在線段FD的延長線上（如圖17）時，∠EGD=60°.當點G在線段FD（如圖18）或DF的延長線上（如圖19）時（但點G不在線段EB或EB的延長線上），∠EGD=120°.

拓展與延伸中考題或幾何素材，對老師而言是開發有限的教材資源、創造性地使用試題素材的舉措之一，對同學們而言是研究性學習的一種有效的方法，不僅可以幫助自己更好地理解知識間的內在聯系，而且可以培養探索數學規律的能力，達到整合知識的目的.同學們運用自己探索發現出來的規律或結論解決問題時，不僅會產生一種成就感，而且會提高對數學這門課程的興趣，在試題的拓展中領會分析問題、解決問題和探究問題的方式、方法，進一步增強學習的主動性、積極性.

用我們教師的無限的智慧與辛勤的汗水，將中考試題的變式、拓展播撒在我們的課堂，讓我們的學生在試題拓展的課堂中自然體驗試題的獨特風韻、新中考的清新容顏.把數學之妙、數學之思、數學之用、數學之美展現在我們精心設計的題組里，讓學生盡情起舞，從容地面對更高、更遠的天空，把夢想與希望放飛，成就人生的精彩.

1.卜以樓.一個幾何模型在中考試題中的拓展與延伸［J］.中學數學（下），2010（6）.

2.吳永剛，董建功.從“無從下手”到“別有洞天”——對一道中考幾何題的研究［J］.中學數學（下），2009（9）.

3.喻漢林.中考數學命題創新的意義與方法［J］.試題研究，2003（2）.

4.曹經富.立足教材習題 注重知識延伸［J］.中國數學教育（初中），2012（7）.

5.曹經富，劉榮堅.與三角形、四邊形有關的變換操作題賞析［J］.中國數學教育（初中），2012（6）.