由一道三角形面積題引發的研究性學習

☉安徽省馬鞍山市二中實驗學校 陳婷婷

☉安徽省馬鞍山市外國語學校杭仁禮

由一道三角形面積題引發的研究性學習

☉安徽省馬鞍山市二中實驗學校 陳婷婷

☉安徽省馬鞍山市外國語學校杭仁禮

新課程改革的核心是課程改革，而課程實施的基本途徑是課堂教學.那種片面強調知識傳授的“填鴨式”教學既背離了培養創新人才的大方向，也低估了學生自身所蘊藏的學習的創新意識和積極性.其實，每一位學生自身都蘊藏著創新的潛能，這需要我們的培養和發掘，要發掘學生的創新思維和能力，就要整合教師、學生、內容和環境之間的關系.而研究性學習注意的是教師、學生、內容和環境四個方面的優化與整合.這樣的教學才是充滿活力的、生長性的、個性張揚的、和諧的課堂，才能真正把學生蘊藏的創新思維與創新能力發掘出來.學生也歡迎這樣的教學改革，因為他們從中可以學到分析和探究問題的能力，也得到研究和發現的樂趣.

一、例題呈現及解答

例題 已知△ABC的三邊長a=5，b=12，C=13，求△ABC的面積.

解：因為a=5，b=12，c=13，

不難發現52+122=132，

所以三邊滿足a2+b2=c2的關系，

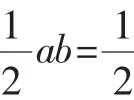
本題的設計意圖是想讓學生用勾股定理先判斷△ABC為直角三角形，再用三角形面積公式求解，同學們很快完成了任務.到這里，本應該結束，進入到下一題，但是隨著學生的一聲提問，使得問題的深度不斷加深.

學生1：如果△ABC的三邊不滿足勾股定理，構不成直角三角形，對于任意△ABC，能否用其三邊a，b，c來表示其面積呢？

二、對問題的一般性研究

1.引領歸納，探究新知

在對原來的問題進行研究之后，隨即對學生1進行了表揚，此時這位同學熱情十足，大家也紛紛思考起來.

在學生1總結歸納完之后，課堂上同學們議論著、探求著、思索著，有時聽到學生的歡呼——數學如此美麗！公式如此優美！

2.遷移類比，真假難辨

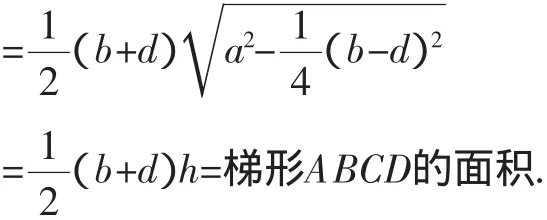
這次的驗證結果又一次支持了我們的猜想.但是，如果換成一般的梯形，結論又不成立了.這些對對錯錯的結果給我們虛虛實實的感覺，無法辨別真假，究竟我們從中能得到哪些啟示呢？由我們驗證的結果看，我們的猜想一定不是一般四邊形的面積公式，而是某一類四邊形的面積公式，考查我們驗證正確的矩形和等腰梯形，你能發現它們有什么共性嗎？

學生5：它們都是軸對稱圖形.

學生6：它們的各邊中垂線都相交于一點.

學生7：它們都是圓的內接四邊形.

三、歸納總結，課后反思

經過同學們課上和課下的討論和思考，得出如下結論，現整理如下：

這堂課本身是一堂預設與生成不一致的研究型學習案例，作為一名一線教師，應大膽鼓勵學生的這種探究精神，保護動態的課堂生成過程，為學生創設一個和諧的、可持續發展的、生機勃勃的課堂氛圍，為他們的思維活動留下發展的空間.這樣的教學也使得學生在相互探索、交流、小組活動中，彼此切磋解題技能，鍛煉思維能力，使學生在鼓勵中創新，在鼓勵中求變，從而實現互利雙贏的教學目標.FH