從一道檢測題審視數學試題的命制

☉江南大學附屬實驗中學 龐彥福

☉江南大學附屬實驗中學 潘海燕

☉江蘇省無錫市南湖中學 葛紅兵

從一道檢測題審視數學試題的命制

一、問題的提出

☉江南大學附屬實驗中學 龐彥福

☉江南大學附屬實驗中學 潘海燕

☉江蘇省無錫市南湖中學 葛紅兵

八年級期中考試的數學試卷上，一道選擇題引來同學們一陣熱議和爭論.筆者拿來試卷饒有興趣地看了一下，該題目是：

顯然，這是一道用來全面考查學生對全等三角形的幾種判定方法掌握情況的一個“不錯”的選擇題，考查的關鍵是根據圖形和條件，觀察、判別角與邊的位置關系是否符合判定的條件.對題目的評價，不僅教師有發言權，學生也會有自己不可小覷的看法.

二、學生的困惑

為此筆者找來了一位成績不錯的學生進行詢問.

筆者：數學考試的時候，同學們感覺試卷怎么樣？

學生：有一道題我覺得好像有問題似的？龐老師，您看就是這道題是不是沒有答案呀？浪費了我不少時間！

筆者：你認為呢？

學生：因為公共邊AD=AD，當∠ADB=∠ADC，BD= DC時，利用SAS可證明△ABD≌△ACD，所以B正確；當∠B=∠C，∠BAD=∠CAD時，利用AAS可證明△ABD≌△ACD，所以C正確；當BD=DC，AB=AC時，利用SSS可證明△ABD≌△ACD，所以D也正確；因此，排除下來就選擇A了.但是，細想想，選項A也能證明△ABD≌△ACD.

筆者：當初為什么選擇A呢？

學生：沒有SSA這個判斷方法，兩邊和其中一邊的對角對應相等的兩個三角形不一定全等.

筆者：你為什么又能夠說明選項A也能證明△ABD≌△ACD？

學生：連接BC，如圖2，由BD＝DC得到∠1＝∠2.

又∠3＝∠4，可以得到∠ABC＝∠ACB，所以就得到AB＝AC.

再利用SSS就可以證明△ABD≌△ACD.

……

從上述對話可以看出，學生的思考、認識和理解都是很清晰的，推理過程也是完全正確的.為了謹慎起見，筆者用幾何畫板進行驗證，當得到如圖3的情形時，顯然△ABD與△ACD不全等，但是這已經偏離了試題本身考查的本意.由這個圖形可以看出，從某種角度來考慮滿足選項A（即∠B＝∠C，BD＝DC）的條件可能會得出兩個圖形不全等，但并不能說明此題沒有問題.該題提供的是圖2的情形，通過添加輔助性，進行二次全等的證明確實能證明△ABD與△ACD全等.

筆者在網上搜索一下，找到了這道題目的“原型”，是2011年南昌市中考試卷的第10題，與期中考試的題目不同的是原題多了兩個字“直接”，原題是“不能直接證明△ABD≌△ACD的是”.僅兩字之差，意義已經不同，漏洞隨之產生，這充分體現了數學的嚴謹性.

三、試題命制的原則

《課標（2011年版）》在“評價建議”部分指出：“評價的主要目的是全面了解學生數學學習的過程和結果，激勵學生學習和改進教師教學.評價應以課程目標和課程內容為依據，體現數學課程的基本理念，全面評價學生在知識技能、數學思考、問題解決和情感態度等方面的表現.”考試是最常見的一種評價方式.數學試題的命制應遵循一些基本的原則，體現數學學科的特點和思想.關于數學題目，章建躍博士認為：“真正的數學題應該滿足一些基本條件，例如：反映數學本質，與重要的數學概念和性質相關，不糾纏于細枝末節，體現基礎知識的聯系性，解題方法自然、多樣，具有發展性，表述形式簡潔、流暢且好懂等.”

1.科學性

數學是嚴謹的科學，題目的編制與呈現應當遵循數學的原理和規律，準確把握試題的基礎性與科學性，不違背常理，體現數學的真正價值.命題應體現課標理念，科學性和嚴謹性是最基本的要求.根據考試的層次不同（如月考（有的學校或地方還有“周考”）、期中聯考、縣（區）級統考或調研測試、學期末測試、學年末測試、模擬、中考等），試題命制的要求和規格也會不同.階段性測試往往更重視基礎性、針對性、易錯點等.

譬如學習過等腰三角形之后，筆者設計了這樣一個題目：已知等腰三角形一腰上的高與另一腰的夾角為40°，那么這個等腰三角形的頂角度數為________.

設計這個題目不僅是為了考查學生對分類討論思想的理解，而且還要考慮到學生對等腰三角形的概念的理解及掌握情況.如果同學們對三角形的分類不能信手拈來的話，就未必能考慮到銳角等腰三角形和鈍角等腰三角形兩種情況（直角等腰三角形顯然不符合題意），從而出現漏解的現象，同時也能進一步固化鈍角三角形的高.數學學習打好基礎是很重要的，基礎是進一步學習和發展的基石，數學學習需要理解，需要學會思維的方法.

2.適宜性

學生是有差異的，學校不同、班級不同，命制試題的難易程度當然是有區別的.對于基礎好的學生做的試卷，如果拿來給基礎薄弱的學生當作考試卷，能不難嗎？基礎不一樣，接受的能力當然是有區別的，如果還用同一標準進行衡量、評價當然是不適宜的.《課標（2011年版）》明確指出：“評價結果的呈現和利用應有利于增強學生學習數學的自信心，提高學生學習數學的興趣，使學生養成良好的學習習慣，促進學生的發展.評價結果的呈現，應該更多地關注學生的進步，關注學生已經掌握了什么，獲得了哪些提高，具備了什么能力，還有什么潛能，在哪些方面還存在不足.”因此，階段性的測試考試試卷的命制與設計要充分考慮學生的實際情況，命制出合理的、適宜的、有針對性的試卷，才能有利于發現教師教學中存在的問題，有助于發現學生學習過程中的遺漏或制約因素，更好地為教師的教學及學生的學習提供改進的措施.

3.規范性

試題由題設到提問，作為一個整體，必須嚴謹無漏洞，不產生歧義，不存在邏輯上的錯誤，不會引起考生不必要的猜測和誤解，才能保證考試的正常發揮，否則會降低考試的功能和效度.數學試題的命制必須符合數學的規范要求.

4.導向性

考試試題的命制要有明確的指向性.考試是為了檢查過去的教與學，更是為了指向今后的教與學.

請看2012年麗水市中考數學試題填空題中的壓軸題：

如圖4，在梯形ABCD中，∠A=90°，∠B=120°，AD=，AB=6.在底邊AB上取點E，在射線DC上取點F，使得∠DEF=120°.

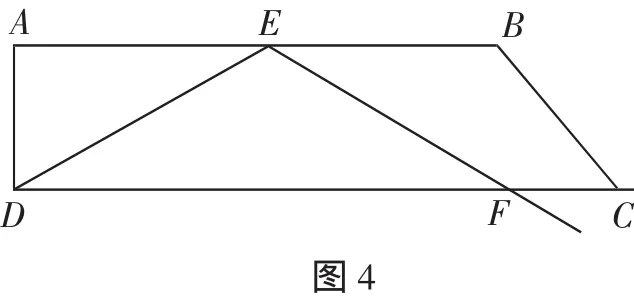
（1）當點E是AB的中點時，DF=________；

（2）若射線EF經過點C，則AE=________.

第（1）問比較容易得出.

解得x=2或5.故答案為2或5.

四、試題命制的方法

考試試卷上的題目來源是有多種渠道的，遴選和改編試題是命制試題的核心性工作.考題可以是教科書上的原題，可以是教材（包括教輔用書）內容、各地測試題、中考題的改編題，可以是命制者的原創題.無論是哪類題都要認真考慮，仔細推敲，避免出現科學性錯誤或與實際不相符合的表述.

1.制定雙向細目表

凡事預則立，無預則廢，試題命制也應如此.首先要從思想上認識到命制試卷的重要性，要明白“命題”和“組卷”的區別，命制試卷體現的是責任心，是業務水平.命制試卷時，應該先制定雙向細目表，依據課標、教材等教學內容與擬考試的內容有效地進行融合，將要考查的內容、知識點以最恰當的方式呈現出來.選題不能“眉毛胡子一把抓”，一份試卷題量有限，基本題，中等題，較難題比例要適宜，既要涵蓋學生應該掌握的主要知識點，又要把重要的核心知識點充分體現出來，把學生容易弄錯的地方暴露出來，把引領教學導向的思想方法彰顯出來.

2.精選原題

教科書選擇的題目基本上是教育教學專家及課程專家經過深思熟慮而選定的，具有一定的代表性、典型性和普適性，各種類型的考試都可以選擇一定量的教材中的原題作為考試試卷中的題目.譬如：

設AB、CD是⊙O的兩條弦，AB∥CD，若⊙O的半徑為5，AB=8，CD=6，則AB與CD之間的距離為_____________.

這是“圓”一章中的一個經典題目了，不同版本的教科書都曾出現過類似的“影子”，或是填空，或是選擇，或是解答.命制試卷選用這樣的經典題目對教學也是一種導向，意在引導我們的教學要重視課本，立足課堂，注重基礎.當然，作為選擇題或填空題時，要變化一下教科書中的數據，以免有的學生剛剛做過且記住了答案，就不思考了.

3.改編試題

改編試題的方法有很多，同樣一道題目經不同的老師改編后的結果也會各種各樣.但無論怎么變化，評價試題質量優劣的標準是該題的科學性、合理性以及有效性，其質量和水平是教師專業能力的體現.將已有的一些現成的好題經過適當改編形成新的試題，改編題可以來源于陳題、舊題，可以是課本上的例題、習題、資料典型題、熱點問題為主，力求“問題在書外，而根在書本”，讓人感到能在課本中找到問題的“影子”，也可選一些學生常常出現錯誤的題目.

下面是利用黃金分割改編的問題.

如圖5，已知AB=1，點C是線段AB的黃金分割點（AC＞BC）.

（1）試用一元二次方程的求根公式求出黃金比.

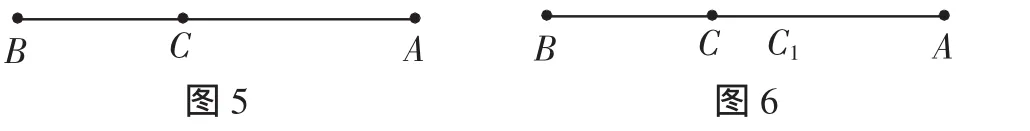
（2）如圖6，取線段AC的黃金分割點C1（AC1＞CC1），計算BC1的長度，并據此判別點C1是否為線段AB的另一黃金分割點.

4.原創試題

好的原創題往往是一份試卷的亮點，原創題的立意更為重要，一個立意好的原創試題，既能正確地診斷出學生在學習過程中存在的知識漏洞和認知方法上的欠缺，還能為學生參加大型考試積累過程性經驗，更能有效地引領學生的學習和思考.原創題要以學生已有知識經驗為基礎，立意新穎，著重考查學生發現和提出問題的能力、分析和解決問題的能力.

命制試題與課堂教學一樣，是一門藝術，而且是一門遺憾的藝術.對于平時的階段性考試或者是區域性的學業水平測試來說，有機會參與命題的老師，應該珍惜機會，做到細心思考、苦心經營、精心設計.在命制試題時，切實把握好數學的科學性、嚴謹性和實用性.因為一份考試卷既是考查學生的學情反饋，更是發展教師引領教學的風向標.

1.符永平，劉東升.命題應該追問“數學”［J］.中學數學（下），2013（7）.

2.章建躍.發展數學的內在力量，為學生謀取長期利益［J］.數學通報，2013（2）.

3.鐘珍玖，龐彥福.初三數學總復習策略再探——談二輪復習的選題原則、方法和評價［J］.中學數學（下），2013（11）.

4.中華人民共和國教育部制定.義務教育數學課程標準（2011年版）［M］.北京：北京師范大學出版社，2012.

5.龐彥福，鐘珍玖，武益燕.從解題策略審視運算錯誤［J］.中學數學（下），2013（8）.

6.龐彥福.教師寫作的素材從哪里來［J］.中學數學數學參考（中），2012（10）.FH

·江蘇省南通市符永平名師工作室·