讓解題思路來的更自然些——從兩道高考題說起

☉浙江省象山中學 祝益鋒

讓解題思路來的更自然些
——從兩道高考題說起

☉浙江省象山中學 祝益鋒

筆者在做2013年遼寧高考卷（理科），發現遼寧兩道壓軸題考生得分不高，筆者認為得分低的主要原因是學生未能較好的掌握通性通法，而這又是因為有相當一部分教師在教學或研究中有意或無意的顯示自己在解題方面的“特技”，不注重對學生通性通法的指導，使學生受到潛移默化的影響所致，學生看到這些題目時首先考慮的不是通性通法，而是特殊技巧，思路混亂，解題時一旦遇阻就毫無章法.借此筆者談談在數學解題中怎樣使解題思路自然而然地展開，少一些技巧，多一點自然.

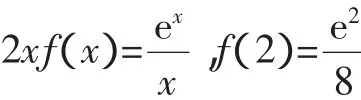
A.有極大值，無極小值

B.有極小值，無極大值

C.既有極大值又有極小值

D.既無極大值也無極小值

上述的解題思路說明一個道理：自然而然、水到渠成的解題過程，常常源自思維方法上的質樸！

（2）若f（x）≥g（x）恒成立，求實數a的取值范圍.

本文主要分析第（2）問，我們先看給的標準答案（摘錄部分）如下：

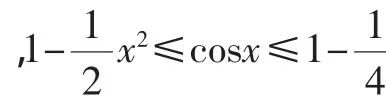
感悟：《數學新課程標準》明確指出：“注重提高學生的數學思維能力.”人們在解決問題時，經歷了猜想，再著手驗證的過程，從局部到整體，層次分明，逐次漸進，并且后者與前者有密切的邏輯聯系，就像爬坡一樣拾級而上.思路也隨著問題的出現而逐漸深入，但每步都是那么自然和順利成章.當我們遇到“難題”和新穎的試題而一籌莫展無從下手時，不妨先把問題簡化一下，以突出其關鍵信息，特別地“把一個比較復雜的問題，‘退’成最簡單最原始的問題，把這個最簡單、最原始的問題想通了、想透了”，然后再歸納、綜合而實現飛躍，“這是學好數學的一個訣竅”.解答任何一個有困難的數學問題都應該從簡單的情形開始！教育數學的先行者張景中院士一向主張為教育而數學，改造數學使之更適宜于教學和學習，解題數學何嘗不是這樣，讓解法是自然的，平易近人的.

但是，有些教師在解題中過于渲染解題技巧，至于技巧怎么來的，其中又蘊含著怎樣的數學思想方法，往往不作解釋，或語焉不詳，讓人只能停留在“欣賞”層面，不會產生心領神會的心靈共鳴.筆者認為從基本概念、原理出發，以基礎知識為依托、以基本方法為技能，按照既定的步驟，逐步推出問題和解答，解法思想順乎一般思維規律，其具體操作過程應該為多數學生所掌握.

題3（2008年浙江高考第8題改編）已知cosα+2sinα=，求tanα的值.

許多文章都對此題做了多種解答，不乏有精彩的，但又有些值得商榷，比如有導數法，左右兩邊求導得出，-sinα+2cosα=0，tanα=-2，馬上得出結果，解法之快，不得不佩服，但此方法是否具有“普適性”呢？請看下面同樣是浙江省的高考題：

如果用導數法，此方法在此題中就失靈了.這兩題都是考查基本的兩角和正、余弦公式，所以自然的想法就是逆用正、余弦公式，解法如下：

當然還有其他解法這里不再例舉.

正如著名數學史學家M.克萊因曾說，“把函數的連續性說成是一條可以用鉛筆不間斷移動所畫出的曲線，比起ε-δ的定義來，要容易掌握得多啊！”，“數學學科并不是一系列的技巧，這些技巧只不過是它微不足道的方面：它們遠不能代表數學，就如同調配顏色遠不能當作繪畫一樣.技巧是將數學的激情、推理、美和深刻的內涵剝落后的產物.”

用最簡單的、最直觀的方法說明最深刻的道理，才是數學之精髓，才是大道.

1.王芝平，王敬華.讓解題思路來的更自然一些［J］.數學通報，2013（2）.

2.章建躍.注重通性通法才是好數學教學［J］.中小學數學（高中版），2011（11）.