關注知識交匯 解析高考難題

☉重慶市梁平實驗中學 蔣明建

關注知識交匯 解析高考難題

☉重慶市梁平實驗中學 蔣明建

高考試題常在“知識網絡的交匯點、思想方法的交織線和能力層次的交叉區”內命題，2013年重慶高考數學理科卷選擇題中的壓軸題第10題便是經典一例.該題新穎別致，獨具匠心，注重能力立意，區分度好，是整個試卷中的一道難題、更是一道創新型試題，很有研究價值，本文將從多個角度作出解析，供讀者參考.

一、試題呈現

評注：這是一道向量（字母表示形式）條件下，求線段長度（向量模）取值范圍的試題，不但考查平面向量垂直、加法的幾何意義、兩點間的距離、不等式的性質等基礎知識，還交匯融合了代數、三角、幾何等多方面知識，同時考查了轉化思想、數形結合思想，及邏輯思維能力、綜合運用知識分析問題和解決問題的能力.

二、解法探究

向量綜合性問題與其他知識的聯系、融合交匯，往往通過向量的幾種不同表示形式來體現，換句話說，向量的不同表示形式關聯著不同數學內容、運算形式及思維策略，因此，對本題向量條件進行有效的分析及合理轉換，把內容與形式結合起來思考、把方法與概念轉化配合起來推進，能獲得廣闊的解題思路，多途徑求解本題.

1.向量運算法則下的解析

解析1：向量字母作伴，幾何法則運算：通常，題設中給出的向量表示法，就是我們解題的首選方法.本題給出的是字母表示法，因此，字母表示法就成了解題的首選.

2.與代數融合——向量坐標形式下的解答

評注：這是最近一些真題卷上最為多見的一種解答.這種解法中，求x2+y2的上界是運用基本不等式進行放縮變換，分別求得x2與y2的范圍后相加而得，將向量坐標運算與基本不等式有機融合一體.這里，運用基本不等式進行放縮變換對能力有較高的要求，一般不容易想到，會造成學生對運用這種解法的困難，筆者覺得這種解答并沒有真正體現出坐標法的優勢，有必要優化.

評注：挖掘發現點B1、B2在圓O：（x-x0）2+（y-y0）2=1上，從而利用圓方程的解析式確定點O（x0，y0）坐標的范圍，比解析2來得自然、容易些，使得解答得到一定程度的簡化，能有效考查學生觀察、聯想、轉化問題的能力.其實，解析2、解析3都囿于考慮動點O的坐標取值范圍，而范圍涉及到不等關系，對于不等關系的建立往往是學生感到困難的事情.能否不求范圍呢？還可以進一步優化.

評注：“增加思考量，減少運算量”是高考能力型試題對考生的要求，要尋找簡捷而高效的解決問題的方法，就要求考生能抓住問題的實質，能對試題提供的信息進行分撿、組合、加工.通觀各個代數式，整體代換得到2-，直接利用關系式求解，避免了解析2、解析3中求點O坐標范圍的繁難步驟，大大簡化了解題過程，充分顯現了向量代數運算簡便快捷的優勢，也培養了我們處理問題的整體意識和全局觀念.

3.與幾何交匯——幾何背景下的研究

蘇聯著名數學家柯爾莫戈羅夫說過：“只要有可能，數學家總是盡力把他們研究的問題從幾何上視角化.”平面向量“數”的特征，賦予向量具有數的良好運算性質，“形”則能體現向量的直觀位置特征.本題幾何背景明顯，可以從幾何角度解答.

解析5：回歸平面幾何 復雜問題簡單化：本題實質是在向量背景下的平面幾何問題，若將整個問題從向量背景中剝離出來，就是一個典型的平面幾何求線段長度取值范圍的問題，于是，可以直接運用平面幾何知識解決.

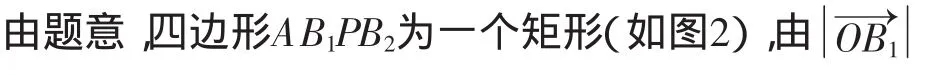
評注：將問題從向量背景中剝離出來，轉化為平面幾何問題，回歸到問題的本源，是一種以退求進的解題策略.它將一個上位問題轉化成了下位問題，把復雜問題化為了簡單問題，由處于上位水平的認知，居高臨下去認知一個下位的問題，使得我們對問題的認識更全面、更深刻、更本質，也使得我們對問題的解決變得更加自然容易，游刃有余.“把簡單的事做復雜是浪費，把復雜的事做簡單是貢獻”，我們要學會把復雜變成簡單，用智慧創造“簡單”，讓思維在探索變遷中不斷的優化和升華.

三、提煉升華

上面從多個角度，運用多方面知識與多種方法，對試題進行了探究解析，其中解析1、4、5中三次重現我們發現運用這一關系式所得到的解答顯得要更為簡潔.那么，這一關系式是本題特有結論還是蘊藏著某種一般規律？進一步探索發現，這竟是一個平面幾何中的一般結論：

定理：平面上一點到矩形一條對角線兩端點的距離平方和等于到這個矩形另一條對角線兩端點的距離平方和（證明略）.

（可類比推廣到三維空間得結論：空間中一點到矩形一條對角線兩端點的距離平方和等于到這個矩形另一條對角線兩端點的距離平方和）（證明略）.

由此，我們便揭開了本試題的神秘面紗，識得“廬山真面目”，它實際背景來源于平面幾何這個定理，只不過將這個定理“穿上了”平面向量這件美麗迷人的“外衣”.由于平面向量具有“形”“數”的雙重身份，它是聯系多個知識點的媒介，更是中學數學知識的一個交匯點，素有“與代數融合、與幾何交匯、與三角聯姻”的美稱，因而，經典幾何問題與富有“親和力”的向量有機融合，幻化而成了這道充滿無限活力與魅力的試題.表面上看，考查的知識點僅限于平面向量垂直、加法的幾何意義、兩點間的距離、不等式的性質等，實質上試題的綜合性很強，要得到正確解答，需要較強的能力支撐、思想積淀與智慧付出.對于功力深厚不乏靈感的考生，若能深入思考分析、挖掘出問題中隱藏的“定理”本質，捕捉到問題的“靈魂”，直接運用定理求解，則是件易如反掌的事情，因而，優生差生立可區分.如此看來，這道高考試題的確是命題老師的“用心良苦”之作，智慧之作，不失為高考試題中的上佳之品.

四、解題反思

數學高考命題注重學科的內在聯系和知識的綜合性，注重從學科的整體高度和思維價值的高度考慮問題，在知識網絡交匯點設計試題，旨在加強對能力和素質的考查功能，突出能力立意的導向作用，它要求考生對課程內容能夠融會貫通，把重點放在系統地掌握課程內容的內在聯系上，放在運用分析問題的方法和解決問題的能力上.因此，在平常的教學中，特別是在復習應考中，要重視基本能力與綜合能力的培養，切實做好“兩個抓住”，一要抓住知識的交匯：綜合能力的提高在于知識交匯處進行訓練，復習中應該特別關注知識內容的“交匯點”，重視其形成，理清其脈絡，分析其內涵、外延和交匯特點，將各部分知識縱向聯系起來認識問題、分析問題、處理問題，重視對綜合問題的強化訓練，在訓練中學會綜合，在綜合中提高能力，從而進一步增強我們綜合解決問題的能力；二要抓住問題的反思：對一些數學題目，特別是像本文中這樣典型的高考題目，要在解決問題的過程上下功夫，在“精”字上下功夫.解題后一定要做好對本題的回顧、反思、提煉和總結，回顧解題所用到的知識點，反思解題方法的遷移與推廣，總結問題內在聯系與區別，深挖細究，揭示問題的深刻本質，力求回歸到問題的本源認識問題等等.只有這樣，我們才能對問題透徹把握，才能做到舉一反三，才能讓我們的思維在靈活性、廣闊性、深刻性、創新性等方面得到充分鍛煉，培養綜合能力，實現“通過解有限道題來獲取解無限道題的那種數學機智”，增強對高考創新型試題的適應能力.

1.蔣明建.破解向量難題，挖掘潛在信息［J］.中學數學（上），2013（5）.

2.蔣明建.一道高三調研考題解答策略的探討與優化［J］.數學通訊，2012（11）.

3.吳祥成.2012年上海高考立體幾何填空題的解法探究［J］.數學通訊，2013（4）.