在解題中體驗成功 在解題中提升思維

☉江蘇省海安縣曲塘中學附屬初級中學 劉鳳蘭

在解題中體驗成功 在解題中提升思維

☉江蘇省海安縣曲塘中學附屬初級中學 劉鳳蘭

題目 （2013年江西卷）某數學活動小組在作三角形的拓展圖形，研究其性質時，經歷了如下過程.

（1）操作發現.

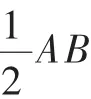
（2）數學思考.

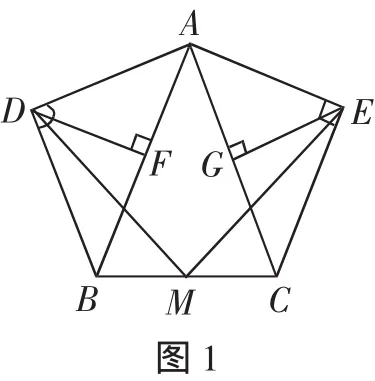
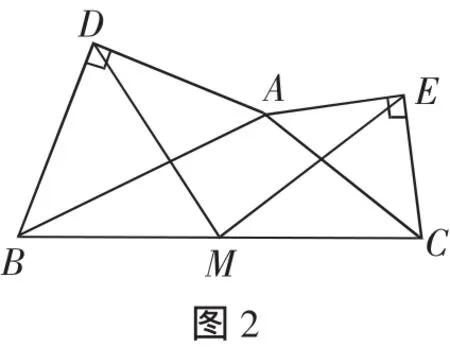
在任意△ABC中，分別以AB和AC為斜邊，向△ABC的外側作等腰直角三角形，如圖2所示，M是BC的中點，連接MD和ME，則MD和ME具有怎樣的數量和位置關系？請給出證明過程.

（3）類比探索.

在任意△ABC中，仍分別以AB和AC為斜邊，向△ABC的內側作等腰直角三角形，如圖3所示，M是BC的中點，連接MD和ME，試判斷△MED的形狀.

解析：（1）①②③④.

（2）MD=ME，MD⊥ME，

（Ⅰ）MD=ME.

如圖4，分別取AB，AC的中點為F，G，連接DF，MF，MG，EG.

所以MF=EG.

同理可證DF=MG.

因為MF∥AC，

所以∠MFA＋∠BAC=180°.

同理可得∠MGA+∠BAC=180°

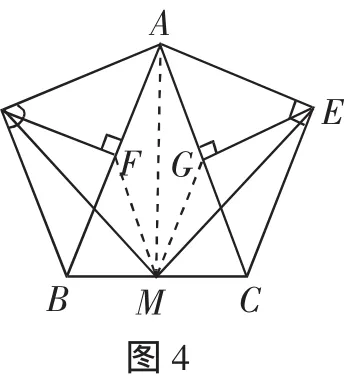
所以∠MFA=∠MGA.

又因為EG⊥AC，所以∠EGA=90°.

同理可得∠DFA=90°，所以∠MFA+∠DFA=∠MGA=∠EGA，即∠DFM=∠MEG.

又MF=EG，DF=MG，

所以△DFM≌△MGE（SAS），所以MD=ME.

（Ⅱ）MD⊥ME.

證法一：因為MG∥AB，所以∠MFA+∠FMG=180°.

又因為△DFM≌△MGE，所以∠MEG=∠MDF.

所以∠MFA+∠FMD+∠DME+∠MDF=180°，其中∠MFA+∠FMD+∠MDF=90°，所以∠DME=90°.即MD⊥ME.

證法二：如圖5，MD與AB交于點H.

因為AB∥MG，所以∠DHA=∠DMG.又因為∠DHA=∠FDM+∠DFH，即∠DHA=∠FDM+90°.

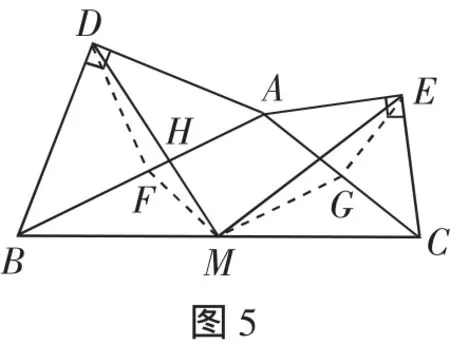
因為∠DMG=∠DME+∠GME，所以∠DME=90°，即MD⊥ME.

（3）等腰直角三解形.

評注：此題以課題學習為藍本，循序漸進、層層深入，形成問題串，考查學生合理猜想的數學感覺與構建數學模型，以及數學歸納、抽象、概括等能力.（1）由圖形的對稱性易知①、②、③都正確，④∠DAB=∠DMB=45°也正確；（2）直覺告訴我們MD和ME是垂直且相等的關系，一般由全等證線段相等，受圖1中△DFM≌△MGE的啟發，應想到取中點構造全等來證MD=ME，證MD⊥ME就是要證∠DME=90°，由△DFM≌△MGE得∠EMG=∠MDF，△DFM中三個角相加為180°，∠FMG可看成三個角的和，通過變形計算可得∠DME=90°.（3）只要結論，不要過程，由（2）合情推理知為等腰直角三解形.解決問題的關鍵是取中點，利用“三角形中位線”、“直角三角形斜邊上的中線等于斜邊的一半”創造條件，構造全等三角形，對能力要求很高.

解完此題，筆者不僅聯想到數學大師波利亞在《怎樣解題》一書中所寫：“沒有任何一個題目是徹底完成了的，總還會有些事情可以做.在經過充分的研究和洞察以后，我們可以將任何解題方法加以改進，而且無論如何，我們總可以深化我們對答案的理解.”你能在別的什么題目中利用這個結果或這種方法嗎？反思此題的圖形特征與解法，果有所獲，愿與大家分享.

1.拓展

再以BC為斜邊，向△ABC的外側作等腰直角三角形，會有什么結果？

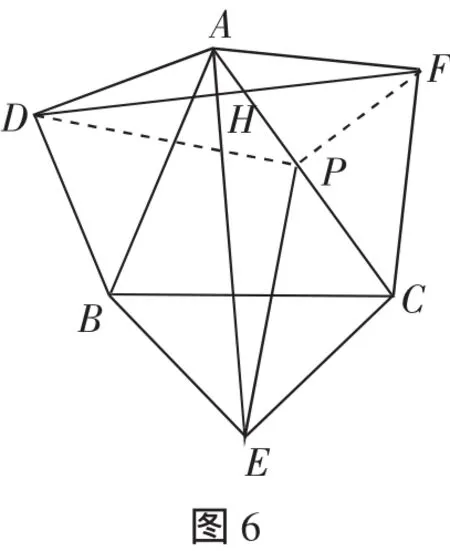
例1 如圖6，分別以銳角△ABC的邊AB、BC和AC為斜邊，向△ABC的外側作等腰Rt△ADB、等腰Rt△EBC和等腰Rt△FAC，求證：AE=DF，AE⊥DF.

證明：取AC的中點P，連接DP、EP.

仿上例可證PD=PE，PD⊥PE.

因為△AFC是等腰直角三角形，所以PF=PA.

因為∠DPF=∠APD+∠APF，∠APE=∠APD+∠DPE，又因為∠APF=∠DPE=90°，所以∠DPF=∠APE.

所以△DPF≌△EPA（SAS），所以AE=DF.

由△DPF≌△EPA，得∠DFP=∠EAP.

因為∠DFP+∠AFD+∠FAP=90°，

所以∠EAP+∠AFD+∠FAP=90°.

所以∠AHF=90°，即AE⊥DF.

2.推廣

將等腰直角三角形改為有一對角相等的直角三角形，會有什么結果？

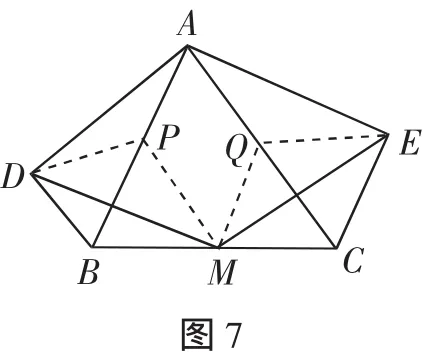
例2 如圖7，以△ABC的邊AB和AC為斜邊，向△ABC的外側作Rt△ABD和Rt△ACE，且使∠ABD=∠ACE=α，M是BC的中點，求證：DM=ME，∠DME=2α.

證明：分別取AB，AC的中點P，Q，連接DP，MP，MQ，EQ.

所以∠DME=∠DMP+∠PMQ+∠QME=∠MEQ+∠MQC+∠QME=180°-∠CQE.

而∠CQE=180°-∠QCE-∠QEC=180°-2α，所以∠DME=2α.

3.變式

將例2的圖形結構作些變化，又會有什么結果？

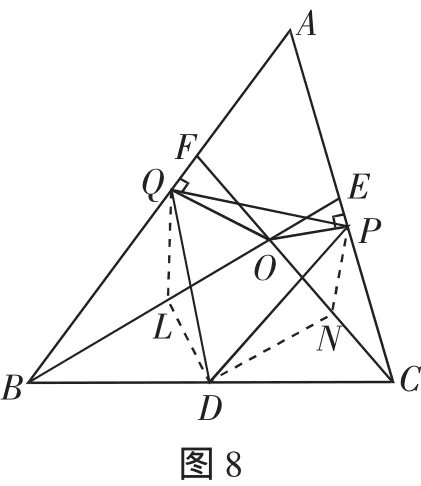
例3 如圖8，在△ABC中，D為BC的中點，點E、F分別在邊AC、AB上，并且∠ABE=∠ACF=30°，BE、CF交于點O.過點O作OP⊥AC，OQ⊥AB，P、Q為垂足.

求證：△DPQ為等邊三角形.

此題是例2的變式，僅僅是題目的表述作了些變化，證明方法相同，本文不再贅述，有興趣的讀者可參照圖8中的輔助線加以證明.

4.結語

本文的四道題既有一定的難度又有密切的關系，帶來的教學、解題啟示是：學習幾何一定要善于積累，解完題后對所做的題盡可能全方位、多角度反思，從變化中抓住不變因素，從復雜的背景中識別圖形特征，從紛繁的干擾中弄清問題的本質，進行歸納、分類，找出規律做好“積墊”，才能胸有成竹、遇題不慌，游刃有余地破解幾何難題，在解題中體驗成功，在解題中提升思維.FH