運算簡單往往要付出邏輯思維的代價——兼說“正難則反”的求解策略

☉河北省唐山市路南區中學教研室 李姝俠

運算簡單往往要付出邏輯思維的代價
——兼說“正難則反”的求解策略

☉河北省唐山市路南區中學教研室 李姝俠

近來關注各地2013～2014學年第一學期期末考試試題，雖然整體上仍然以迎合中考的拼湊中考題試卷為主，但也能見到一些地區命題者匠心獨具，設計出一些具有鮮明導向的優秀試題.本文挑選兩道有一定難度的考題，嘗試給出不同解法，并反思這類考題帶來的教學導向和命題思辨，與同行研討.

一、兩道“期末考題”的解法突破

下面結合兩個不同地區、不同年級的期末考題，講解不同解法，一起感悟不同解法的差異.

例1 （江蘇省某縣七年級2013～2014學年第一學期學業測試卷）一批樹苗按下列方法依次由各班領取：第一班取100棵和余下的110，第二班取200棵和余下的110，第三班取300棵和余下的110……最后樹苗全部被取完，且各班的樹苗都相等，求樹苗總數和班級數.

難點分析：問題要求的兩個未知量“樹苗總數”、“班級數”，如果只設一個未知數，該設哪個？方程的等量關系何在？這些都很困難.

第1種思路：設樹苗總數為x棵，可列出方程：

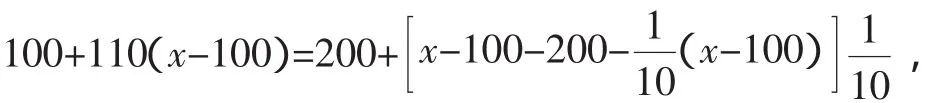
解得x=8100.

問題獲得突破.

解后反思：從上面的等量關系獲得一個繁雜的方程，促使我們繼續尋找其他的思路.

第2種思路：列表來簡化問題的文字表達：

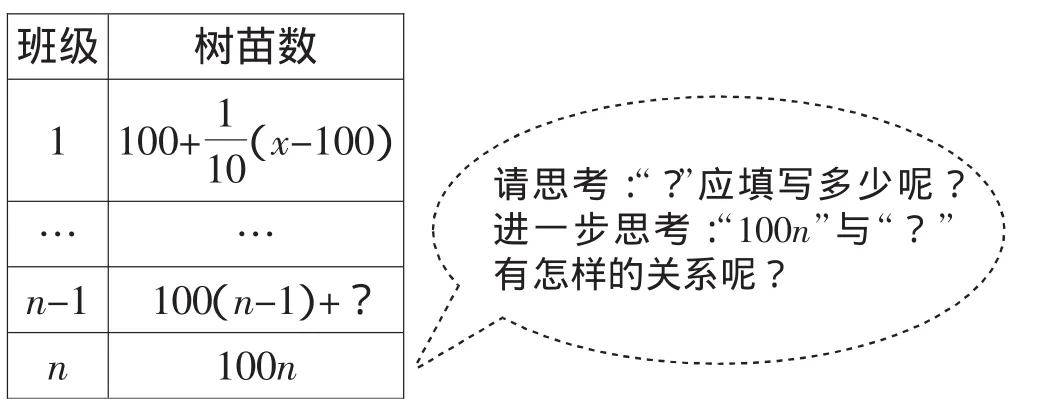
班級 樹苗數1 100+1 10（x-100）……n-1 100（n-1）+？n 100n請思考：“？”應填寫多少呢？進一步思考：“100n”與“？”有怎樣的關系呢？

經過上述分析，“？”應該是100，于是可設“？”為110m，且有100n=910m.

問題獲得貫通，即m=1000，100n=900.

所以n=9，x=8100.

解后反思：上述常規思路涉及較繁雜的數式運算與變形，需要對數式變形有較高的運算適應性，才能在高危害的考場環境下成功突破，對考生的心理、運算能力有一定的挑戰.考慮到本題中拋物線、圓均涉及對稱性，這會啟發我們嘗試簡化問題的求解，下面給出第二種思路.

第2種角度（基于對稱角度思考）：如圖4，由（2）知C是弧MN的中點.在半徑DN上截取EN=MG，又因為DM=DN，所以DG=DE.則點G與點E關于點D對稱.連接CD、CE、PD、PE，由圓的對稱性可得圖形PMC的面積與圖形PECN的面積相等.

由PC把圖形PMCN（指圓弧MCN和線段PM、PN組成的圖形）分成兩部分，這兩部分面積之差為4，可知△PCE的面積為4.

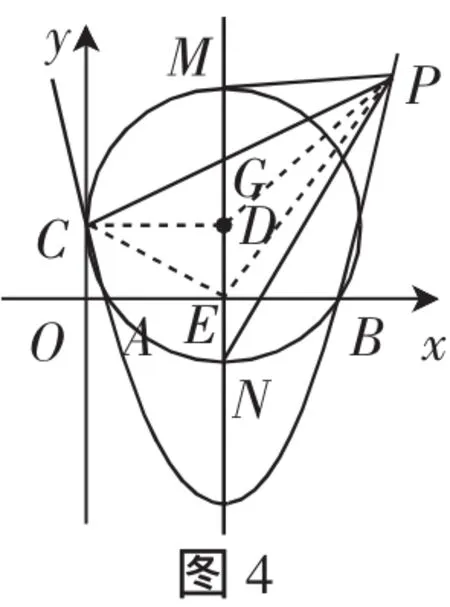
點評：第2種思路雖然較之第1種思路的步驟、運算大為減少，但是基于對稱啟示的輔助線（半徑DN上截取EN=MG）、△PCE的面積為4、S△CEP=2S△CDP等的洞察，都是有較高難度的，與例1一樣，解法的簡潔需要付出大量邏輯思維的代價.

二、兩點思考

1.“正難則反”的解題策略值得推介

先說一段數學史上關于“正難則反”的經典故事：歐幾里得的名著《幾何原本》中有一條公理，歷史上稱之為“第五公設”——同平面內一條直線與另外兩條直線相交，若在某一側的兩個內角的和小于180°，則這兩條直線經無限延長后在這一側相交.由于這個“公設”在敘述上不像其他公理那樣簡明，并且在書中證明第29個命題時才遲遲用到它，以后就再也不用了.這促使人們思考：第五公設能否用其他公理及前28個命題來證明？經過1000多年的努力，人類沒有成功，雖然曾有很多人宣布獲證，但是有錯誤的論證……1000多年的試證失敗，引起了許多數學家的思考：證明第五公設是可能的嗎？于是，許多數學家反設“第五公設”不成立，往前推，希望推出矛盾的結論.確實，否定“第五公設”導致了許多“怪異”命題，如三角形的內角和小于180°，矩形不存在，半圓的圓周角為銳角等，但它們與否定第五公設并不矛盾.實質上，這是另一種幾何—非歐幾何（高等數學的內容）.正面證明沒有成功，反而又否定不出矛盾，數學似乎走到了進退兩難的境地，其實不然，這將迎來了一場數學上的革命.1826年2月23日，俄國數學家羅巴切夫斯基在喀山大學物理數學系宣讀了他的論文《幾何學原理的扼要闡述暨平行線定理的一個嚴格證明》，宣告“第五公設”是能證明的，否定“第五公設”的另一種幾何（非歐幾何）是存在的.學習非歐幾何是大學的事，但非歐幾何誕生過程中的“正難則反”的思想卻處處有用.上文的兩個題例中的第二種“簡化思路”也體現了“正難則反”的求解策略.

2.高危害的考試中設置此類試題應慎重

《義務教育數學課程標準（2011年版）》關于“評價建議”有如下表述：“評價的主要是目的是全面了解學生數學學習的過程和結果，激勵學生學習和改進教師教學.”“評價不僅要關注學生的學習結果，更要關注學生在學習過程中的發展和變化.”作為平時學期內的學業水平練習或反饋，像上文中“例1”、“例2”這樣的考題設置，能啟發學生思考、改進教師教學，加強解題教學中的反思和優化取向，讓師生在測試后能得到后續的發展或改進.但是，在中考或“一考定終身”類的高危害考試中，設計這樣的試題需要慎重考慮，因為考生在應對此類問題時，一般都是以獲得常規思路貫通后即展開演算、表達，在很緊張的考試時間（我國數學考試的一個顯著不足：時間短、題量大）難以抽身做解法或思路的優化.這樣勢必造成這類問題設計的考查意圖、信度、效度降低，這事實上就涉及了“好題”往往并一定適合在考場上用的道理.

1. 史寧中.基本概念與運算法則——小學數學教學中的核心問題［M］.北京：高等教育出版社，2013.

2. 中華人民共和國教育部制定.義務教育數學課程標準（2011年版）［M］.北京：北京師范大學出版社，2012.