解讀蘇科版數學教材中“數軸”的意義

☉江蘇省宿遷市宿豫區教育局教研室 胡 濱

解讀蘇科版數學教材中“數軸”的意義

☉江蘇省宿遷市宿豫區教育局教研室 胡 濱

關于數軸的意義，義務教育數學課程標準（2011年版）沒有提出明確的教學要求，只是提出“能用數軸表示……”與“借助數軸理解……”等用數軸解決問題的一些具體要求.那么在教學過程中，數軸概念意義的形成與獲得過程是否就應該“弱化”處理呢？其實不然，經教育部審定后的最新蘇科版義務教育教科書七年級（上冊）中的《2.3數軸》教材中，數軸意義的內容呈現比修訂前更加細化、深化、強化了許多環節與內容.對此，我們解讀如下.

一、細化數軸意義的引入內容，突出數學基本觀念的把握

試一試（摘自原教材）：

在小學里，我們會根據直線上一個點的位置寫出合適的數，也會在直線上畫出表示一個數的點.

試把圖1中直線上的點所表示的數寫在相應的方框里.

圖1

這里的“試一試”有兩個作用，一是回顧經驗，二是激活經驗.因為我們的一切知識都是建立在經驗之上，而且最后是導源于經驗的.在已有的小學數學經驗上，我們認識到的數學對象有：根據直線上的一個點的位置寫出合適的數；這種直線上的點是依次排列的；可以在直線上畫出表示一個數的點；這樣的直線幫助我們認識自然數的大小關系.當借助數學經驗感知這些有一定層次的數學對象時，三個數學基本觀念——“直線”、“點”、“數”就隨即直觀地傳達于我們心中.再深入反思這三個基本觀念時，我們便獲得了清晰的“數軸”初步概念意義的層次：

直觀感知 直線 點 數深刻反思水平直線，有方向的直線.點布滿了直線，直線上每一個點都表示一個數.每一個數都可以在直線上找到相應的點，點或數的排列受原點和單位長度制約.

所以，在這里的“試一試”數學活動過程中，回顧已有數學經驗是認識數軸的基礎，感知數學對象、獲得基本觀念是數軸概念形成的核心，深刻反思是形成清晰數軸概念層次的關鍵.可以說，數軸概念的形成，得益于能從已有的數學經驗中獲得三個數學基本觀念——“直線”、“點”、“數”，直觀感知與深刻的心理活動是數學基本觀念形成的兩個重要途徑.因此，引入教材內容教學的重點在于，首先能從已有數學基本經驗中提煉出基本數學觀念，其次是能夠深入思考、記憶、整理與使用這些基本觀念，使得“數”在“形”上呈現出可見對象與直觀支撐，最后才能形成完整的數軸概念圖式.這就啟示我們的教學設計應當關注以下幾點：

1.由于圖形的實質是將相對抽象的“數”的思考對象“圖形化”，因此在激活小學數學經驗時，能畫圖時要盡量安排學生畫.

2.剛剛進入初中學習的小學生往往都把注意力消耗在觀察圖形（圖1）上，很少能仔細反省心中對數學對象的感知、以及對數學觀念的剖析上，要加強學習方面的引導與針對性的知識小結.

3.給學生做出“數學書應該這樣閱讀”的示范.即能理解數學對象、數學觀念、數學方法、數學經驗事實的精確含義，特別是隱藏在文字背后的含義，能善于在課文內容的字里行間中發現問題，并就這些問題的提出、分析、抽象、解決和引申作適當的探索.

二、深化數軸概念的表述，突出數軸的“表示”要義

在數軸上，我們看到了“點”可以表示“數”，如“數軸”上的點可以表示數-1，-2，-3，…可以表示數0，可以表示數1，2，3，…可以表示數-2.5，3.5，-1.5，-，，…這說明兩個道理，一是凡能寫成分數形式（m、n是整數，n≠0）的數，都在數軸上；二是數軸上表示有理數的點有“很多”.例如，數軸上兩點A、B，它們所對應的數分別是a、b，那么A、B的中點所對應的數值是，同理可以知道其他兩點的中點所對應的數值，這樣繼續找下去，雖然距離越來越小，但每兩點之間總有一個中點，而且這個中點所對應的數值可以計算出來，它也可以是分數形式.顯而易見，這些點是很稠密的排列在數軸上.

“數軸”上“點”與“數”的關系是相互對應的.這種對應表現為一種意識——面對數學問題能想到利用圖形來思考；其次表現為掌握一定的幾何直觀的畫圖技巧，能畫出數軸并借助數軸圖形進行思考的經歷和經驗，表現為一種能力；想不想畫出數軸、會不會畫數軸圖的問

做一做（摘自原教材）：

1.畫一條水平直線，并在這條直線上取一點表示0，我們把這個點稱為原點.

2.規定直線上從原點向右為正方向（畫箭頭表示），向左為負方向.

3.取適當長度（如1cm）為單位長度，在直線上，從原點向右每隔一個單位長度取一點，依次表示1，2，3，…從原點向左每隔一個單位長度取一點，依次表示-1，-2，-3，…

如圖2，像這樣規定了原點、正方向和單位長度的直線叫做數軸.

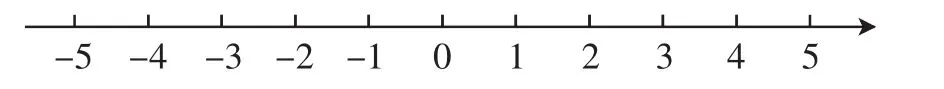
圖2

在數軸上，用原點右邊且到原點的距離是1.5個單位長度的點表示1.5，用原點左邊且到原點的距離是2.4個單位長度的點表示-2.4.

通過具體的“做一做”，得到了“像這樣規定了原點、正方向和單位長度的直線叫做數軸”的帶有操作程序性的意義.當你接受數軸意義內容就是數軸的三要素——原點、正方向、單位長度時，后來關于數軸的一切觀念，就會永遠建立在這個基礎上，至于對數軸意義的深刻理解，則可能是被動的.人類理解理論相關研究指出，人類智力的第一種能力，就在于接受印象，然而就在接受簡單的觀念時，大部分理解是被動的.因此，若想得到數軸的深刻意義，必須借助已經接受的簡單觀念來增進自己的思想能力，以增加自己的知識儲備，以便使自己在回憶、想象、推理和思考時，更能順利地使用數軸的意義圖式.

“數軸”的意義與“直線、點、數”三個數學觀念是相符合的，它的基本特征就是依托、利用圖形進行數學思考和想象.先把研究的“數”抽象為“圖形（點）”，再把“直線、點、數三個數學觀念之間的關系”轉化為“數與形之間的關系”，這樣就把研究“數”的問題轉化為“圖形的數量或位置關系”的問題，加以思考分析.這就是說，數軸知識是直覺的知識，直覺知識是最明白、最確定的，這種確定性完全依賴于直覺.因此，不需要記住它的什么意義、什么三要素，只要求能切實感知到它的直觀，深刻反思它的意義，靈活使用它來解決數學問題.

在這一段課文內容中，出現頻率最高的詞就是“表示”，就是說，數軸的重要作用在于“表示”.“表示”有“表述、表明、標記、借某種事物顯出某種意義”等含義，因此，把握數軸意義的重點在于，借助數軸的“表示”作用不僅能直接看到想要知道的東西，而且還能依托看到的東西進行思考、想象，即不僅看到了什么，而是通過數軸思考到了什么，聯想到了什么.這是一種十分重要而有價值的思維方式.題解決之后，不斷地運用，形成正向的動力定型，逐步會形成一種當遇到抽象理性的問題時，主動地退到適合的層面上去推動思維展開的思維方式.

要使得在具體的教學環節設計上產生預想的教學效果，應當關注以下幾點：

1.準確完成數軸的畫圖，既知道畫數軸的方法，更有嫻熟畫數軸的技能.

2.在數軸上能領悟到數的對立統一規律與數的排列規律.

3.欣賞數軸的和諧美，它把直線、射線、線段有機統一于一體，使有理數與無理數共存于其中，體現了數與形的完美結合.

三、強化無理數的引入過程，突出幾何直觀的重要作用

議一議（摘自原教材）：

面積為2的正方形的邊長a是無理數，如何在數軸上畫出表示a的點？

以原點為一個端點，在數軸上向右畫一條長為a的線段.

a應位于1.41與1.42之間.

做一做：

將邊長為a的正方形放到數軸上（如圖3），以原點為圓心、a為半徑，用圓規畫出數軸上的一個點A，點A表示的數就是無理數.

圖3

怎樣用數軸上的點表示圓周率π？

做一個直徑為1個單位長度的圓片，它的周長為

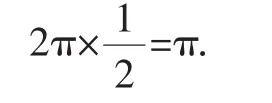
如圖4，把圓片上的點放在原點，并把圓片沿數軸滾動1周，點A到達點A′的位置，點A′表示的數就是π.

圖4

議一議、做一做兩段教材內容揭示了“數軸”與“實數”的關系，其主要內容有：

“數軸”上表示有理數的點，并未布滿整個數軸.數軸上的點還可以表示哪些數呢？如圖3中的點A和圖4中的圓周率π，它們都是無理數.我們若參照圖3，還可以構造出對角線長分別為1，1.5，3，3.5，…無數個正方形來，它們的邊長都是無理數，都可以在數軸上找到相對應的點來表示.就是說，數軸上表示無理數的點也有“很多”，它和有理數一起共同布滿了整個數軸.正如課文內容所表述的那樣：有理數和無理數都可以用數軸上的點表示；反過來，數軸上的任意一點都表示一個有理數或無理數.

“數軸”上并非有理數“多于”無理數.我們若以任一有理點為起點，向右移動與以單位長為邊所作的正方形對角線等長的距離，就可以得到和所有有理點“一樣多”的無理點.但是，我們還可以找出任意多的其他無理點，如以1與2分別為長和寬作一個矩形，其對角線的長為距離的點就是一個無理點，這樣的點還可以按照這種辦法找出很多.每找出這樣一個無理點，又可以再產生與有理點“一樣多”的無理點.這就是說，在數軸上，并非有理數“多于”無理數.

“數軸”上的點可以表示的數有兩類：一類是可以寫成分數形式的有理數，另一類是形如圖3中的點A與圖4中的圓周率π所表示的無理數，即數軸上點可以表示有理數和無理數，表示有理數的點是稠密的，表述無理數的點也是稠密的，它們共同布滿了整個數軸.至此，有關“實數”意義的基本觀念已十分清晰地呈現在我們的面前.對這段教材內容的分析，啟示我們的教學設計應關注這樣幾點：

1.計算無理數值的一般思想，是用有理數逐步逼近的.

2.從有理數出發，用作圖的方法可以得到龐大的無理數家族.有一個無理數a，就可以造出無窮多個無理數來，如2a，a+2等；有一個無理數π，同樣可以造出無窮多個無理數來.這些無理數不過是龐大無理數家族中小小的一支而已.

3.用“作圖”的方法在數軸上找到表示無理數的點，表明兩層意思：一是這種“實驗”是在想象中做的、是設想著做的、是在思想中進行的實驗，在數學中，我們常常使用思想實驗；二是這樣的點只是示意性的，其示意性突出表現在無理數形成的內在機理的數量關系，隨著學習不斷深入，我們會逐漸明白這種示意圖的準確意義.

1.楊裕前，董林偉.義務教育教科書數學·七年級上冊［M］.南京：江蘇科學技術出版社，2013.

2.王國生，張強.中學數學里的數軸［J］.數學通報，1957（2）.

3.［英］洛克.人類理解論［M］.北京：商務印書館，2012.