LTE/W iMAX片上變壓器的分析與設計

張華斌，蔡 敏，武海軍，李正平

(1. 華南理工大學電子與信息學院 廣州 510640；2. 電子科技大學中山學院 廣東 中山 528402；3. 廣州潤芯信息技術有限公司 廣州 510663)

隨著無線通信頻率的提高，集成電路中所使用的變壓器電感值正逐漸減小，從而為芯片中集成變壓器提供更大的可能性和現實性。變壓器由初、次級電感繞組耦合而成，由于耦合作用，其初、次級電感值及品質因子分別比單電感值高(1+k)倍[1]，所以集成電路中使用片上變壓器既可縮小電路的芯片面積，又可提高電路的系統性能。目前，變壓器正廣泛應用于低噪聲放大器、匹配網絡、混頻器、功率放大器等射頻電路中[2-5]。

最新的LTE/WiMAX四代通信芯片模塊開發將繼續縮小芯片面積、降低成本和提高產品性能，需要新的工藝和新的設計方法來滿足射頻電路的各項特性指標要求，但由于所采用的0.13 mm TSMC射頻和混合信號工藝庫中沒有提供相應的變壓器器件及其模型，這給設計工程師設計高性能、低成本的射頻通信芯片帶來很大的困難。鑒于這點，設計出滿足無線通信電路要求的高性能變壓器器件及其高精度模型成為研究的關鍵問題。

近年來，隨著對片上變壓器模型的研究不斷深入，變壓器模型精度隨之不斷提高。文獻[6]提出由兩個簡單的電感模型耦合而成，電感的模型用寄生集總電阻和電感的串聯，加上端口間寄生集總電容，以及與襯底之間的氧化層電容串聯硅襯底本身的電阻和電容的并聯網絡構成，該模型沒有考慮襯底的渦流效應、線圈繞線之間的鄰近效應和線圈本身的趨膚效應。文獻[7]對模型的初級和次級繞組中的寄生電阻加以改進，使其具有頻率相關性，這種變化使得模型包含了趨膚效應和鄰近效應。文獻[3]對模型進一步改進，在初、次級線圈中增加中間抽頭部分，使之成為雙p網絡，同時增加了四個互感系數和兩個端點之間交叉電容，該模型考慮了分布效應、趨膚效應、鄰近效應和襯底的渦流效應。在以后的模型設計中普遍采用雙p結構，該結構具有更高的模型準確性。

文中引用文獻[3]的片上變壓器等效模型，根據最新TSMC射頻和混合信號工藝的厚頂層金屬，高電導率，離襯底距離遠，低介電常數的特點，考慮片上變壓器的幾何圖形對其性能和芯片面積的影響，優化設計出幾款高性能的新八邊形變壓器，并給出了變壓器器件的設計過程、模型參數提取方法和模型參數，采用該方法將有助于無線通信集成電路中集成變壓器的實現。

1 變壓器器件分析

考慮片上變壓器的特點，如文獻[7]中描述有平行繞組(shibata)、交錯繞組(frlan)、疊層繞組(finlay)、同軸螺旋繞組結構。這些結構可分為兩種形式：一種是平面繞組變壓器，如平行繞組結構、交錯繞組結構和同軸螺旋繞組結構。其中平行繞組結構具有中等耦合系數，缺點是不對稱，初、次級端口距離非常近，容易引起串擾，所以這種結構不常用；交錯繞組結構能提供很好的1∶1匝比，中等耦合系數，且初、次級端口分布在版圖兩側，利于級聯；同軸螺旋繞組結構耦合系數很低(k ≈ 0.3～0.5)，插入損耗大，使用范圍有限。另一種是立體的繞組結構，如疊層繞組結構，它有高耦合系數，節省芯片面積，但繞組不對稱，電容相對大的特點。因而用于諧振頻率不高的場合，可有效降低芯片面積。

除了考慮繞組結構以外，設計片上變壓器還要考慮其形狀，不同的幾何形狀所包含的電學特性是不一樣的。片上變壓器幾何形狀主要有方形、六邊形、八邊形、圓形等。這些形狀在以往設計片上螺旋電感時已存在，因此設計片上變壓器時可利用這些圖形。由圖1[8]可知，在同一頻率時，對于具有相等電感值的不同螺旋電感，圓形的品質因子最大，其他八邊形、六邊形和方形的品質因子依次減小。由此推斷在設計片上變壓器時，為了提高該器件的品質因子，必須提高變壓器圖形的邊數，但實際上很多硅工藝都不支持圓形變壓器的設計。

因此，從繞組結構和幾何圖形這兩方面綜合考慮，設計變壓器時應選擇八邊形的幾何圖形和交錯繞組的平面結構。

圖1 固定電感值下不同形狀的品質因子與頻率的關系

2 變壓器等效電路模型和參數計算

2.1 片上變壓器的物理效應和電路模型

變壓器等效電路模型是在電感集總參數等效電路模型的基礎上，考慮初、次級繞組相互之間的耦合效應而建立起來的。片上八邊形變壓器物理效應等效原理如圖2所示，圖中，硅工藝變壓器的每個部分用理想的集總元器件來代替，這些元器件可以清楚地反映出由電場和磁場所引起的多種物理效應。如大量的導體與導體之間以及導體與襯底之間的由電場效應引起的電容；在繞線導體中代表趨膚效應、鄰近效應和渦流效應的頻率相關性的電阻和電感，可以用階梯電阻和電感代替；繞組與繞組之間的感應效應可以用耦合因子代替等。

圖3是片上變壓器SPICE等效電路模型，模型中使用兩個雙p電感等效電路以及感性和容性的耦合，每個電感采用梯型結構，模型具有很好的對稱性。由于模型的對稱特性，初級線圈和次級線圈的兩端間的元器件值相等(如：Cox3= Cox1, Csub3= Csub1，Rsub3= Rsub1)，初級與次級間的耦合系數以及耦合電容值也相等，因此對于這種片上變壓器的雙p等效電路模型，可以根據部分元器件及其參數的對稱性，而自然減少元器件提取的數目。

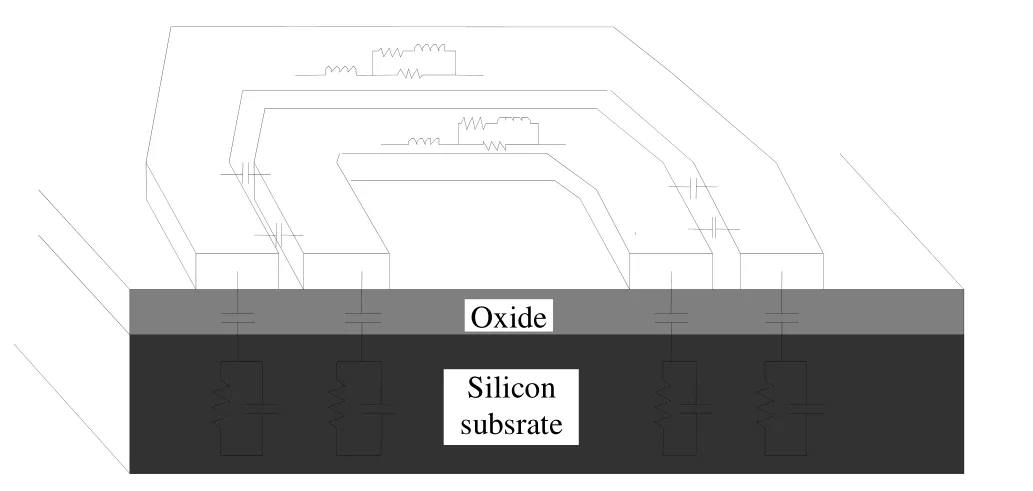
圖2 八邊形變壓器物理效應等效原理圖

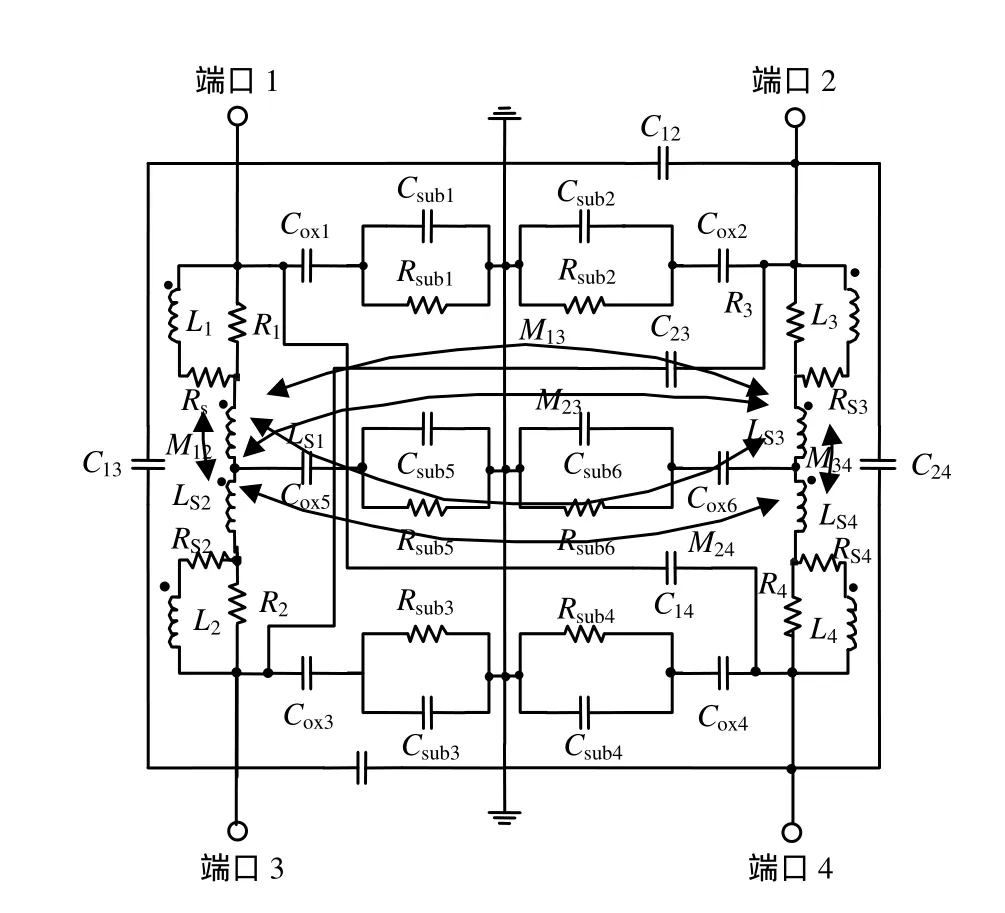
圖3 采用耦合電感模塊的變壓器電路模型(1和3代表初級繞組兩個端口，2和4代表次級繞組兩個端口)

2.2 梯形結構元器件和線圈間耦合系數的計算

變壓器模型中的元器件參數可以通過文獻[3]中提出的解析式計算，圖3中端口1和3之間的初級繞組包含趨膚效應和鄰近效應的梯形結構，端口2和4的次級繞組同樣也考慮趨膚及鄰近效應的梯形電路，模型中梯形結構的無源器件表達式為：

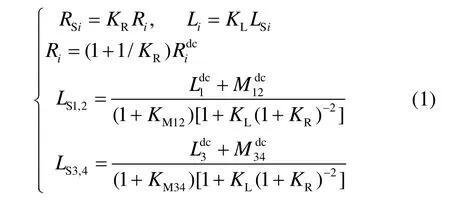
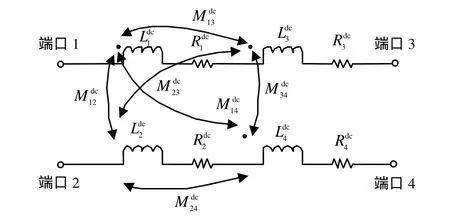
圖4 片上變壓器直流等效電路模型(端口1和端口3代表初級繞組兩個端口，端口2和端口4代表次級繞組兩個端口)

式中，m0為真空中的磁導率；d為平均直徑；w為金屬繞線的寬度；s為繞線間的距離；t為金屬繞線導體的厚度。

由于變壓器等效電路模型中的渦流、趨膚和鄰近效應的物理性質可以用電阻和電感的梯形網絡實現[9]，因此，直流條件下的互感系數KMij也同樣應用于高頻狀態的梯形網絡中。圖3中的變壓器等效電路模型有6個耦合系數，這6個耦合系數的計算方法可用直流狀態下的各個繞線導體間的耦合系數表示，有：

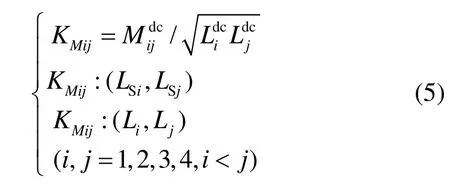
2.3 端口間自感、互感電容參數計算

變壓器中的寄生電容有兩種，一種是相鄰繞組間的繞線電容Cw-w，該電容通過半圈與半圈之間的電容進行計算，然后再累加。另一種是交疊電容Cov，它是兩種不同層的金屬繞線在此處交疊。在單個螺旋的建模中，繞線與繞線間的電容時常可忽略，但在多線圈的變壓器中它的值相對比較大，這是由于每兩個相鄰的繞組分別屬于不同的線圈(初級或次級)。

片上變壓器模型中的電容由自感電容和互感電容構成，分別表示為自感電容C13、C24，互感電容C12、C34、C23、C14，4個互感電容分別屬于初、次級不同的端口，計算時通過對端口處相連金屬導體進行區分。由于工藝尺寸持續縮小，電容計算時要考慮多種效應，圖5表示同一金屬層間兩個極板間的電容Cw-w，計算時除了考慮極板間垂直方向的電容外，還必須考慮邊際電場效應所產生的邊際電容，準確的單位長度電容Cw-w表達式為[10]：

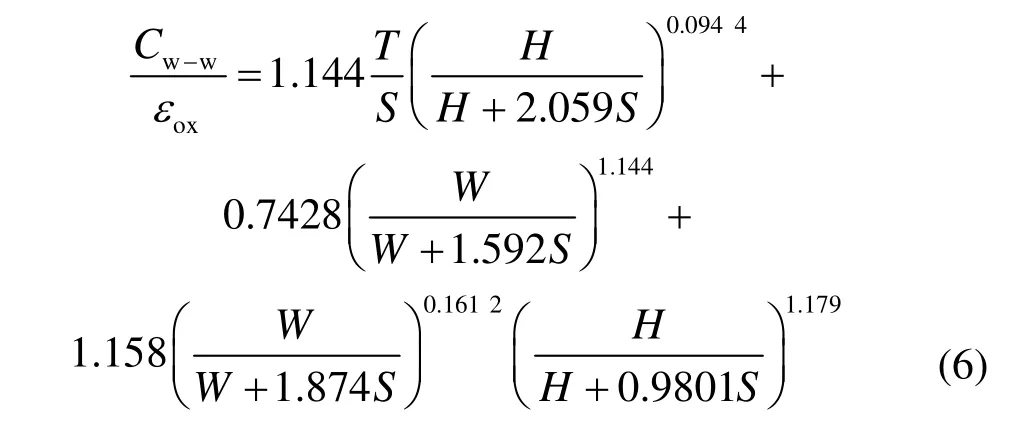
式中，T為金屬繞線導體的厚度；S為繞線間的距離，H為金屬繞線到地端之間的距離；W為金屬繞線的寬度。

不同金屬層間的單位長度的交疊電容Cov的計算，采用考慮邊際電容的極板電容公式：

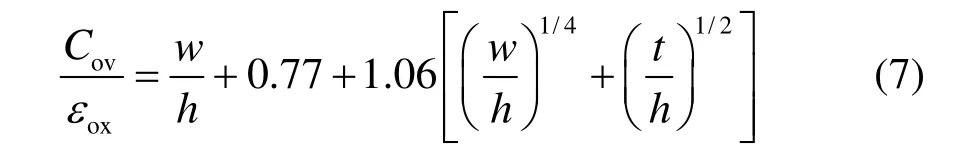
圖5 有限地平面上同層金屬與金屬之間的電容計算結構圖

3 模型驗證和結果分析

圖6為采用0.13 mm 1P8M CMOS射頻和混合信號工藝來制作應用于LTE/WiMAX的3個片上八邊形變壓器，圖中由左向右變壓器繞組線圈匝比分別為4∶4、5∶5和5∶5，通過設計該類型變壓器既可以驗證模型的精確性，又為特定電路設計提供SPICE仿真的參數。設計這些變壓器的關鍵幾何尺寸為：內徑ID，初級圈數Np，次級圈數Ns，線圈(金屬導體)的寬度W，以及線圈(金屬導體)之間的間距S。變壓器繞線層由頂層金屬M 8和次層M 7制作，金屬M 8層作為變壓器的初、次級繞組線圈，其厚度是次層金屬M 7厚度的4倍，有利于降低繞組線圈的電阻值，金屬M 7層由于其厚度相對較薄，電阻值大，僅作為變壓器繞線的交叉走線。

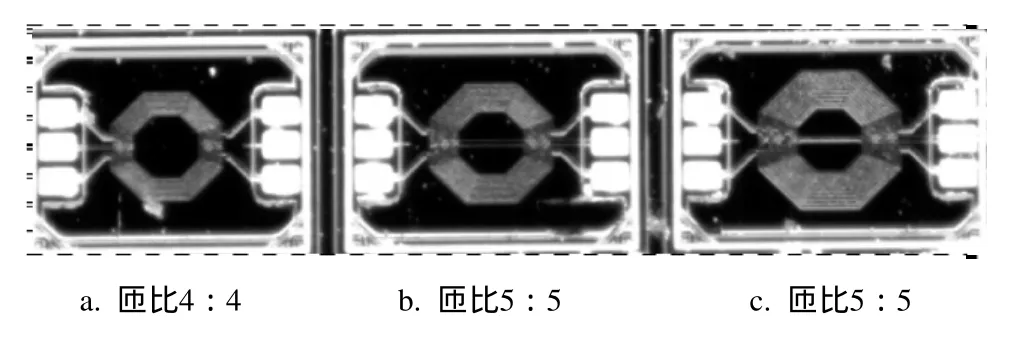
圖6 匝比為n∶n的3種不同自感系數的八邊形變壓器芯片

片上變壓器的測試系統由Cascade M icrotech 11000探針臺、安捷倫E8363B PNA網絡分析儀、以及G-S-G探針組成，測試裝置如圖7所示。在測量圖6中幾個變壓器的兩端口S參數時，為了得到有效的S參數，必須采用測試開路結構和短路結構去嵌的方法來去除原S參數中所包含的壓焊塊和互聯線寄生效應，從而得到準確有效的變壓器S參數[11-13]。

圖7 八邊形變壓器在片測試系統

根據變壓器流片的工藝參數和模型參數計算公式，提取了圖6b部分，變比為5∶5的變壓器模型參數，如表1所示。為了驗證模型的準確性，仿真數據必須與測量數據作全面的比較，對于變壓器器件來說主要考慮的特征參數有：初、次級繞組線圈的電感值，初、次級繞組線圈的品質因子和變壓器的耦合系數。關于這些特征參數，可通過對變壓器所提取的有效S參數進行處理，將之轉化為阻抗和導納參數，抽取變壓器中的初級和次級繞組線圈的電感值(L11、L22)、品質因子(Q11、Q22)以及變壓器的耦合系數(k)，并通過這些參數來評估所設計的變壓器總體性能。

表1 變比為5∶5的變壓器等效電路模型參數

圖6a所示的變壓器設計物理參數為：初、次級繞組線圈匝數比為4∶4，內直徑為134 mm，繞線寬度為4 mm，線間距為2.1 mm，其中，線間距為設計規則所允許的最小間距。圖8給出該變壓器的初、次級繞組線圈電感L和品質因子Q隨頻率變化的測量與模型仿真曲線，這些曲線表明其測試結果與模型數據在0～14 GHz頻率范圍內具有良好的一致性，從而驗證了變壓器模型的有效性。變壓器的初級直流電感值為5.48 nH，諧振頻率為5.57 GHz，品質因子在設計工作頻點處為10.16，幾乎與峰值10.17一致。變壓器的次級線圈Q值比初級稍高，表明次級線圈的阻值比初級線圈的阻值稍低，但變壓器初次級仍然顯示出較高的對稱性。

圖9b為初、次級繞組線圈的電感和品質因子與頻率關系的曲線圖。該變壓器繞組的匝比為5∶5，其他物理參數與樣品一相同。圖9給出在0～10 GHz頻率范圍內變壓器初、次級線圈電感和品質因子的模型和測試數據曲線，這些曲線表明設計的模型和測試數據的一致性。因此，設計所提供的模型在一定的頻率范圍內不僅能夠反映實際器件特性，而且可應用于電路中進行SPICE模型仿真。該變壓器的初級直流電感值為7.60 nH，諧振頻率為4.82 GHz，品質因子在設計工作頻點處為9.58，幾乎與峰值9.61一致，表明所設計的變壓器工作于最佳狀態。

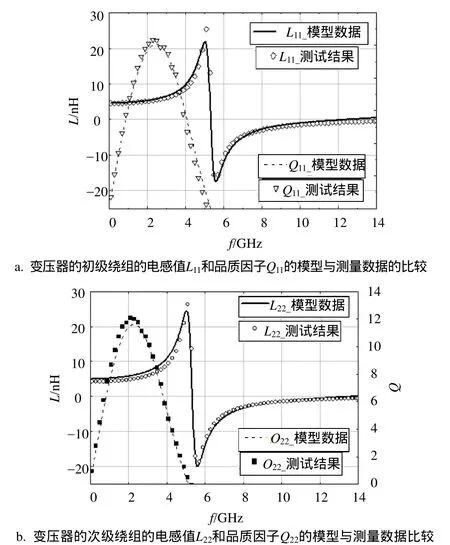
圖8 匝比為4∶4的變壓器的初、次級繞組線圈電感L和品質因子Q隨頻率變化的測量與模型仿真曲線

圖10是圖6a和圖6b所示的變壓器繞組線圈的耦合系數與頻率關系曲線，兩個樣品的模型數據和測試結果在頻率范圍內具有很好的一致性，表明該模型能夠準確地反映器件的物理特性。無論是圖6a所示的變壓器還是圖6b所示的變壓器，其耦合系數都隨著頻率的增加而增大，在頻率低于3.2 GHz時，圖6a所示的變壓器的耦合系數大于圖6b所示的變壓器的耦合系數，表明在同樣的圖形結構下，匝比4∶4的變壓器比5∶5的變壓器耦合系數大，磁耦合能力強。其中，在工作頻點上圖6a所示的變壓器的耦合系數為0.850，圖6b所示的變壓器的耦合系數為0.806。

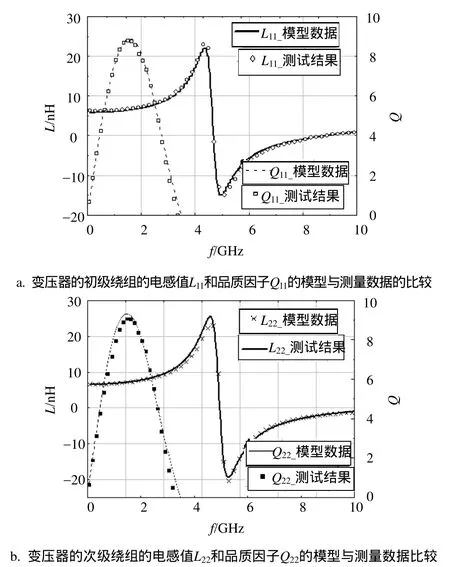
圖9 匝比為5∶5的初、次級繞組線圈的電感和品質因子與頻率關系曲線圖

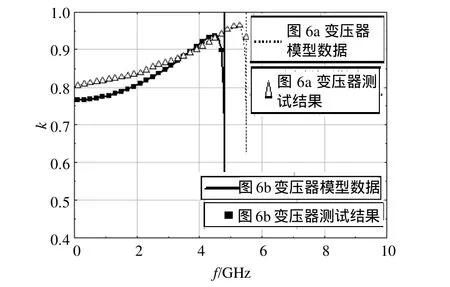
圖10 圖6a和圖6b的變壓器耦合系數模型數據和測試結果比較

4 結 論

本文針對TSMC 0.13 mm RF CMOS射頻和混合信號工藝器件庫中無變壓器器件，在考慮工藝設計規則和研究變壓器器件高性能的基礎上，開發出用于LTE/WiMAX射頻通信集成電路的八邊形片上變壓器，并提出了一種集總元器件變壓器等效電路模型。為了驗證器件的性能和等效電路模型的有效性，本文對變壓器器件進行了流片測試，測試結果與模型數據相比在0.1～10 GHz頻率范圍內，初、次級的電感系數、品質因子和耦合系數具有良好的吻合性。此外，在工作頻點變壓器的耦合系數達到0.80以上，表明片上變壓器具有良好的耦合效果。該片上變壓器設計成功，可以方便地將其用在SPICE射頻電路仿真器中，有助于4 G通信芯片的開發和應用。

[1] ALY A H, BEISHLINE D W, SHARAWY B E. Filter integration using on-chip transformers[C]//The 2004 IEEE M ITT-S International M icrowave Symposium Digest. Fork Worth: IEEE, 2004(3): 1975-1978.

[2] AHN H R. Modified asymmetric impedance transformers(MCCTs and MCVTs) and their application to impedance-transforming three-port 3-dB power dividers[J].IEEE Transactions on M icrowave Theory and Techniques,2011, 59(12): 3312-3321.

[3] GAO Wei, JIAO Chao, LIU Tao, et al. Scalable compact circuit model for differential spiral transformers in CMOS RFICs[J]. IEEE Transactions on Electron Devices, 2006,53(9): 2187-2194.

[4] JEN Yung-nien, TSAI Jeng-han, HUSNG Tian-wei, et al.Design and analysis of a 55~71 GHz compact and broadband distributed active transformer power amplifier in 90-nm CMOS process[J]. IEEE Transactions on M icrowave Theory and Techniques, 2009, 57(7): 1637-1646.

[5] 李萌, 余志平. 用于CMOS射頻集成電路中多級放大器級間耦合的片上變壓器的設計方法與2模型[J]. 清華大學學報(自然科學版), 2011, 51(3): 328-333．

LI Meng, YU Zhing-ping. Design methodology and modeling of an on-chip transformer for inter-stage coupling for multi-stage amplifiers in CMOS RFIC[J]. Journal of Tsing hua University ( Sci & Tech) , 2011, 51(3): 328-333．

[6] ZHOU J J, ALLSTOT D J. Monolithic transformers and their application in a differential CMOS RF low-noise amplifier[J]. IEEE Journal of Solid-State Circuits, 1998,33(12): 2020-2027.

[7] LONG J R. Monolithic transformers for silicon RF IC design[J]. IEEE Journal of Solid-State Circuits, 2000, 35 (9):1368-1382.

[8] MOHAN S S. The design, modeling and optimization of on-chip inductor and transformer circuit[D]. Stanford:Stanford University, 1999.

[9] NOBUHIRO S, TORU M, TAKAHIRO N, et al. Scalable transformer model based on ladder topological equivalent circuit for Si RFICs[C]//2010 Topical meeting on silicon monolithic integrated circuits in RF systems(SiRF). New Orleans: IEEE, 2010: 12-15.

[10] WONG S C, LEE T Y, MA D J, et al. An empirical three-dimensional crossover capacitance model for multilevel interconnect VLSI circuits[J]. IEEE Transactions on Semiconductor Manufacturing, 2000,13(2): 219-227.

[11] WANG Chuan, LIAO Huai-lin, LI Chen, et al. A w ideband predictive ‘double-π’ equivalent-circuit model for on-chip spiral inductors[J]. IEEE Transactions on Electron Devices,2009, 56(4): 609-619.

[12] KANG I M, JUNG S J, CHOI T H, et al. Five step(pad-pad short-pad open-short-open) de-embedding method and its verification[J]. IEEE Electron Device Letters, 2009, 30(4): 398-400.

[13] TIEMEIJER L F, PIJPER R M T, HEIJDEN E V D. Two multiport de-embedding methods for accurate on-wafer characterization of 60-GHz differential amplifiers[J]. IEEE Transactions on M icrowave Theory and Techniques, 2011,59(3): 763-771.

編 輯 稅 紅