映射觀下的組合問題

陳明

（遵義師范學院數學與計算科學學院，貴州遵義563002）

映射觀下的組合問題

陳明

（遵義師范學院數學與計算科學學院，貴州遵義563002）

排列組合是中學數學內容中學生普遍感到困難的部分，作者用現代數學語言給出其中組合的解釋和說明.

組合；映射；等價關系；陪集；商集；分類

排列組合在中學數學內容中，是學生普遍感到困難的部分．究其原因，有以下三個方面：首先，內容本身是教學難點；其次，在其定義及表述上難以理解；再次，解題思路及方法難以掌握．作者用現代數學的集合、計數、分類、陪集、商集與映射的觀點及方法，對組合問題作了一些分析、歸納，試圖對組合概念作較高層次的解釋、說明，希望能對中學數學該部分內容的教學有所幫助或提高．

文中所討論的集合均為有限集．為方便，記#A表示集合A的元素個數，Nn={1,2,…n}表示從1開始的n個自然數的集合，I(Nm,A)表示映集Nm到集A所有單射組成的集合．關于集合的映射計數法，可作如下定義

定義 若#A=n，當且僅當存在著一個雙射f:A→Nn．

普通高中數學教材中對組合概念的敘述：

從n個不同元素中，任取m(m≤n)個元素并成一組，叫做從n個不同元素中取出m個元素的一個組合．

如上敘述之關鍵，在于取出的m個元素不存在順序上的問題，并成一組即可．對此，我們設f∈(Nm, A)（其中#A=n），且f(Nm)=B，現如保持B而只改變其元間的順序，顯然，存在這樣的g∈(Nm,A)，且也有g(Nm)=B.這樣，我們給出如下的組合

定義I(Nm,A)中(#A=n)所有的以B為象的單射給出一個“從n事物中一次取m事物的組合”．

另外，若定義I(Nm,A)上的一個關系R，對于f,g∈I(Nm,A)，(m≤#A=n)，當且僅當f(Nm)=g(Nm)時，稱f與g有關系，表為f R g.顯然，關系R滿足自反性、對稱性與傳遞性，故關系R是集合I∈(Nm,A)中元間的一個等價關系．由近世代數知識（張禾瑞《近世代數基礎》28頁定理2）知此等價關系R決定了集合I(Nm,A)的一個分類，每一個類叫做I(Nm,A)的一個陪集，所有陪集作成的集叫做I(Nm,A)的商集，記為I(Nm,A)/R．而每個陪集的意義為“從A中取m個元的組合”．因而，商集I(Nm,A)/R中的每一元也就等價于“n個事物中取個m元的一個組合”．從而計算組合數就只需計算陪集的個數：#(I(Nm,A)/R)．

證明參見文獻[1]中定理1.

推論 在定理1中，當n=m時，#(I(Nm,Nm)=

為了計算組合數，我們首先證明商集I(Nm,A)/R中所有陪集的元素個數均相等．

設f是I(Nm,A)/R中的任一元，因f是I(Nm,A)中的一個單射，這里設f(Nm)=B，顯然，#B=m，且所有以B為象的單射個數，就等于B中m元的亂排數．故由定理1的推論知所有以B為象的單射個數為m！.這樣，我們就推得f所在的陪集fR的元的個數為#f R=m!.又因f是任意的，所以商集I(Nm,A)/R中所有陪集元的個數均相等且為m!.

另外，由分類的定義可知I(Nm,A)由所有兩兩不交的陪集之并集所構成，由前面知陪集的個數用表示．從而有

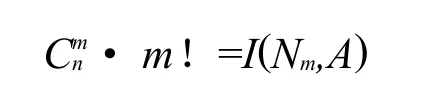
由定理1，有

這樣，我們得到了

定理2從n事物中取m事物的組合數為：

同樣，這與中學課本上的組合數公式也是完全一致的．

以上采用導入方式給出定理．反之，如給出定理讓其證明，那我們又可有如下的證法．

分析由定理2

因此，只需證明商集I(Nm,A)/R中，每一個陪集的元素個數都是m！即可．

證明當m=0時，因故關于模R僅有的陪集是自身．于是

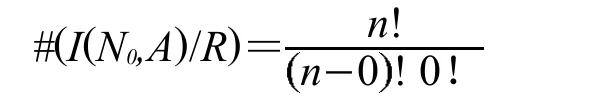
定理2成立．

若m＞0，由分析知，只需證每個陪集中單射的個數為m!即可．

為了證得#fR=m！，因#PermNm=m（!注：PermNm為Nm的全排列），故只需證#fR≈PermNm即可．為此，設法構造一個從fR到PermNm的雙射.

∵PermNm是Nm→Nm

為了達到這一目的，我們固定一個元h∈fR，若g是可逆的，則有

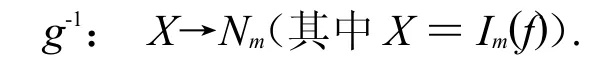
由圖1的線圖可以看出：

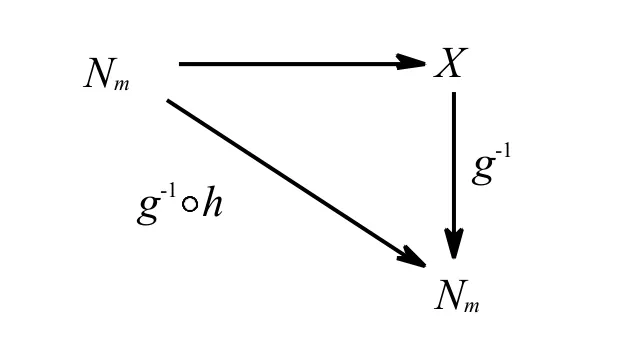
圖1

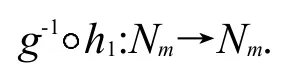
（1）∵g∈I(Nm,A)，∴g∶Nm→X是一對一的；

（2）又∵Im(g)=X∴g是在上的．

由（1）、（2）可推出：g∶Nm→X是一雙射．

故g可逆，即g-1是存在的．從而上面定義的也就確實有效了．

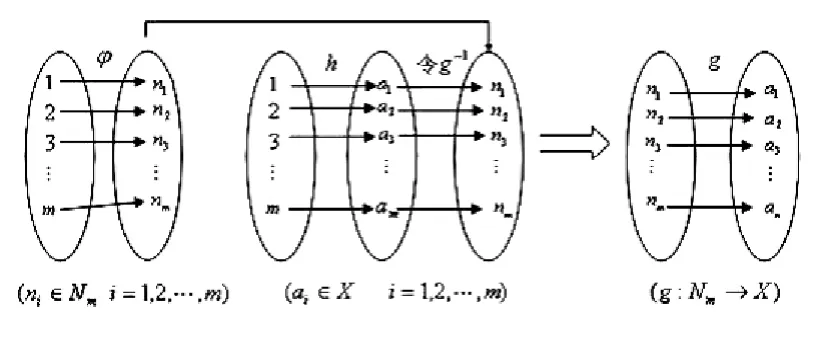
圖2

故由定理1之推論，有

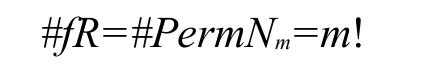
如前所述，這就證明了定理2．

至此，我們利用集合、映射、陪集、計數的觀點對組合進行了解釋和說明．

關于中學數學教材對這一問題所采用的處理方式，主要是出于以下兩方面的原因，一是學生的年齡特點；二是學生的知識結構．本文用現代數學的語言加以闡述，其目的是想說明現代數學與中學數學在這一部分內容上的內在聯系．

[1]陳明.映射觀下的排列問題[J].遵義師范學院學報,2012,14 (6)：81-82.

[2]張奠宙,鄒一心.現代數學與中學數學[M].上海：上海教育出版社,1990.

[3]陳明.排列組合之乘法原理探索[J].黔南民族師范學院學報, 2007,(6)：37-38.

[4]H B格里菲思,P U希爾頓.經典數學綜合教材[M].陳應樞,陳信傳譯.貴陽：貴州人民出版社,1986.

(責任編輯：朱 彬)

On the Combinatorial Problem from the perspective of Mapping View

CHEN Ming
(College of Mathematics and computing science,Zunyi Normal College,Zunyi 563002,China)

Permutation and combination are what high school students feel very hard in the maths contents of high school,and the author of this paper expounds the combination by modern mathematical expressions.

combination;mapping;equivalent relation;coset;quotient set;classification

O157

A

1009-3583（2014）-0104-03

2014-05-13

陳 明，男，貴州遵義人，遵義師范學院數學與計算科學學院副教授。