mBBM方程的含橢圓函數形式的精確解*

劉轉玲

（蘭州商學院信息工程學院，甘肅蘭州 730020）

引言

非線性偏微分方程是數學的一個非常重要的分支，常被用來描述過程控制、生態系統、經濟系統、化學循環系統和流行病學等問題.非線性偏微分方程描述上述問題能充分考慮到時間、空間、時間延遲及其他因素，所以更準確地反映了現實情況.

Benjamin －Bona－ Mahony 在水波研究中提出了 BBM 方程［1，2］，之后發展為 mBBM［3］方程，這個方程是弱非線性色散介質中長波單向傳播的重要模型，因而，對于mBBM方程的深入研究［4］，特別是對于有效地數值計算方法的研究，具有重要的理論和現實意義.

本文的目的是應用Painlevé直接截斷法對mBBM方程的精確求解作深入的探討.

1 直接截斷方法簡解

Painlevé直接截斷方法［5，6］是將Painlevé檢驗中的Laurent級數做有限截斷，其中假定奇性流形函數是具有某種特定的性質，最后，偏微分方程的精確解是通過確定截斷級數的系數來確定.這一方法簡潔直接，在一定范圍內具有相當的普適性.Painlevé直接截斷方法簡述如下.

對于給定的偏微分方程:

式中U（x，t）是一個關于x，t的多項式.假設方程（1）具有

2 橢圓函數的性質

如果f（ξ）和g（ξ）滿足以下橢圓函數的條件:

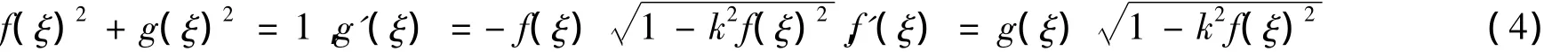
3 mBBM方程的含橢圓函數形式的精確解

4 結論

運用Painlevé直接截斷法，不僅可以求出mBBM方程的其他一些不同形式的精確解，也可求出其他一些偏微分方程的精確解.

［1］洪寶劍，盧殿臣，趙康生.Burgers－BBM 方程新的精確解［J］.應用數學，2007，20（1）:134 －139.

［2］汪裕才.周期邊界條件下B－BBM方程的整體吸引子［J］.應用數學，2004，17（2）:239－242.

［3］陳松林，侯為根.推廣的B－BBM方程和B－BBM方程的顯式精確解［J］.物理學報，2001，50（10）:1842－1846.

［4］郭鵬，張磊，王小云，等.mBBM 方程和Vakhnenko方程的顯示精確解［J］.量子電子學報，2010，27（6）:683－686.

［5］Zhao D，Luo H G，Wang S J，et al.A direct truncation method for finding abundent exact olutions and application to the one －dimensional higher－ order Schrodinger equation［J］.Chaos Solitons and Fractals，2005，24:533 －547.

［6］Zhao D，Luo H G，Chai H Y.Integrability of the Gross－ Pitaevskii equation with Feshbach resonance management［J］.Phys.lett.A，2008，372:5644 －5650.

［7］王明亮，李志斌，周宇斌.齊次平衡原則及其應用［J］.蘭州大學學報:自然科學版，1999，35（3）:8－16.