一維有限深方勢阱中束縛態存在條件的求解*

王 磊

（菏澤學院物理系，山東菏澤 274015）

在許多量子力學教材中，一維勢阱是比較簡單且較早處理的問題，作為量子力學課程的基礎問題曾被廣泛研究［1，2］.對于在一維有限深勢阱中運動的粒子，當其處于束縛態時，確定其能級的是超越方程.各類參考書籍大多用數值解法給出了在一維有限深方勢阱中存在束縛態的條件.本文將通過求解定態薛定諤方程，利用連續函數的零點定理完整地給出在一維有限深方勢阱中粒子能級存在的條件.所用方法與結果簡潔明了，對處理這類問題有普遍意義，既可培養學生綜合運用知識的能力，也可加深對這類問題的理解.

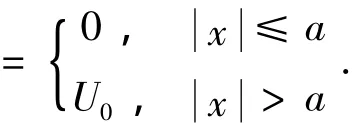
圖1 一維中心對稱勢阱

各分區的定態薛定諤方程［3，4］:

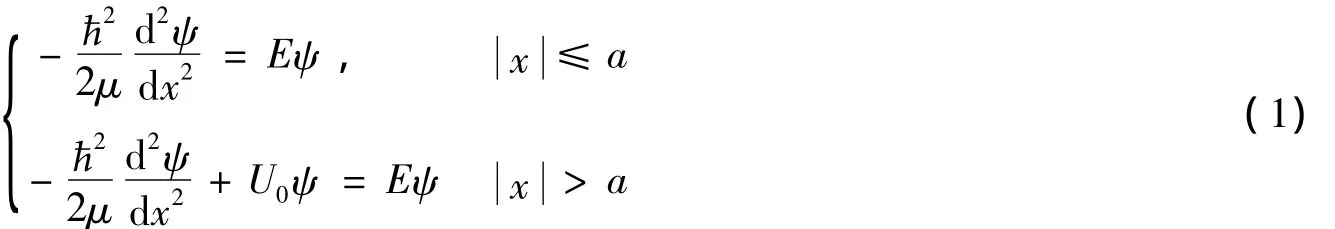
總之，我們通過求解一維中心對稱有限深勢阱中運動粒子的定態薛定諤方程，引入了一個在勢阱內部連續的函數，然后根據連續性函數的零點定理對勢阱中粒子存在束縛態的條件及數目進行了深入分析.方法簡潔明了，易于接受，并能夠鍛煉學生綜合運用所學知識解決問題的能力，加深對此類問題的理解.

［1］易其順.一維無限深勢阱內粒子概率密度演示儀［J］.物理實驗，2010，30（7）:24－26.

［2］符立亞，胡照文，任華蓀，等.一維無限深勢阱的擴展探討［J］.大學物理，2010，29（8）:36－38.

［3］曾謹言.量子力學導論［M］.第二版.北京:北京大學出版社，2008:57－60.

［4］周世勛.量子力學教程［M］.第二版.北京:高等教育出版社，2008:31－38.

［5］四川大學數學系高等教學研究室.高等數學（第1冊）［M］.第3版.北京:高等教育出版社，2006:85－92.

［6］四川大學數學系高等教學研究室.高等數學（第3冊）［M］.第3版.北京:高等教育出版社，2006:96－102.