真空包裝雞肉早餐腸中細菌總數生長預測模型的擬合優度比較

陳 睿，徐幸蓮*，周光宏，王 鵬

（南京農業大學 教育部肉品加工與質量控制重點實驗室，江蘇 南京 210095）

真空包裝雞肉早餐腸中細菌總數生長預測模型的擬合優度比較

陳 睿，徐幸蓮*，周光宏，王 鵬

（南京農業大學 教育部肉品加工與質量控制重點實驗室，江蘇 南京 210095）

為比較不同生長預測模型對真空包裝雞肉早餐腸中細菌總數生長情況的擬合效果，觀察在不同貯藏溫度（2～15 ℃）下，使用Baranyi、修正的Gompertz及修正的Logistic模型分別描述細菌總數隨時間變化的情況，以及使用Arrhenius方程與平方根模型描述一級模型所得參數隨溫度變化的情況。通過計算各模型的評價參數（均方誤差平方根RMSE、回歸系數R2、赤池信息準則與貝葉斯信息準則），參考模型所得特征值及貨架期殘差值，評價各模型的擬合優度，尋找最優組合。結果表明：Baranyi模型所得方程的評價參數最優，最大比生長速率（μmax）最大，所得產品貨架期殘差值較小；應用修正的Gompertz模型更有利于優化二級模型評價參數；而修正的Logistic模型擬合所得初始菌數N0值偏小，且將15 ℃貯藏組延滯時間λ計算為負值。因此Baranyi模型的擬合優度最高，其次為修正的Gompertz模型，最后為修正的Logistic模型。應用Arrhenius方程與平方根模型均能夠成功擬合，但未能得出擬合更優者。

預測模型；擬合優度；溫度；比較

微生物生長預測模型通過擬合軟件，根據產品中微生物數量變化狀況可建立數學模型來描述微生物生長。預測模型可分為一級模型、二級模型與三級模型[1]。其中一級模型為微生物生長模型，二級模型為微生物生長動力學模型，三級模型則是整合了一級模型與二級模型的應用軟件。微生物生長預測模型的建立不僅能夠監控產品在流通貯藏期的微生物生長情況，還可為產品貨架期預測模型建立提供重要依據，在食品生產與流通等領域具有廣泛的應用前景。

由于各級模型的函數種類繁多，而對于不同的產品及細菌種類，不同的函數擬合結果有所差異，而擬合優度[2]（goodness-of-fit）可通過比較模型均方誤差平方根（root mean square error，RMSE），回歸系數R2，赤池信息準則（Akaike information criterion，AIC），與貝葉斯信息準則（Bayesian information criterion，BIC）[3]等數值描述這些差異，從而對擬合模型的優劣程度進行評價。通過比較不同模型函數的擬合優度，選擇適合產品的預測模型函數十分重要。關于模型的擬合優度評價方法，國外已有許多經驗，如Slongo等[4]分析了回歸系數R2、均方誤差MSE、偏差因子Bf與準確因子Af的變化；Juneja等[5]比較了均方差、皮爾遜系數、BIC及AIC等數值的差異；Mataragas等[2]計算了殘差平方根和回歸系數等。但目前國內關于預測模型擬合優度的比較研究主要以畜禽生長曲線為對象，缺乏以微生物生長曲線為對象的比較研究[6-9]。

本實驗以雞肉早餐腸在2～15 ℃貯藏中細菌總數的變化情況為研究對象，通過計算模型特征值、影響因子及貨架期預測殘差值，分別比較修正的Gompertz模型、修正的Logistic模型和Baranyi模型的擬合優度；通過計算模型特征值與影響因子，分別比較平方根模型、Arrhenius方程的擬合優度，為產品選擇適合的預測模型函數，從而為估測產品貨架期提供更有效的幫助。

1 材料與方法

1.1 材料與試劑

雞肉早餐腸由江蘇某大型肉食品公司提供，100 g/袋真空包裝。

氯化鈉（分析純） 南京化學試劑有限公司；平板計數瓊脂、無菌拍打袋 北京陸橋技術有限責任公司。

1.2 儀器與設備

HVE-50型高溫高壓滅菌鍋 日本株式會社平山制作所；MP5002型電子天平 上海舜禹恒平科學儀器有限公司；SPK-250B-Z型生化培養箱 上海博迅實業有限公司醫療設備廠；DHC-964385-Ⅲ型電熱鼓風干燥箱上海新苗醫療器械制造有限公司；SW-CJ-2FD型潔凈工作臺 蘇凈安泰公司；拍打器、Scan1200型自動影像分析菌落計數儀 法國Intersicence公司；移液器 德國Eppendorf 公司。

1.3 細菌總數計數

無菌操作準確稱取2、6、10、15 ℃貯藏的樣品各25 g，移入無菌拍打袋，向拍打袋中加入225 mL已滅菌0.85 g/100 mL的生理鹽水，封口放入拍打器中，以中高速拍打2 min。取1 mL菌液進行10 倍梯度稀釋，選擇3 個合適的稀釋梯度，每個梯度做3 個重復，傾注平皿（平板計數瓊脂）。倒置平皿，于37 ℃培養箱放置48 h。使用菌落計數儀進行計數。

1.4 數據處理

采用Microsoft Excel進行數據整理，采用軟件Origin 9.0擬合模型的方程，采用軟件SPSS Statistic 20.0進行單因素方差分析（最小顯著差異法）。

1.5 一級模型的擬合

一級模型主要描述在特定環境或培養基條件下，微生物數量與時間變化的關系。根據一級模型擬合得到的方程可推算得出微生物生長動力學相關參數，包含最大生長速率、遲滯時間、初始微生物數量以及最大微生物數量。

1.5.1 修正的Gompertz模型

Gompertz模型屬于經驗模型，是美國農業部開發的病原菌模型程序（pathogen modeling program，PMP）和英國農業、漁業和食品部開發的食品微型模型 （food micromodel，FM）的基礎模型。其函數表達式為[10]：

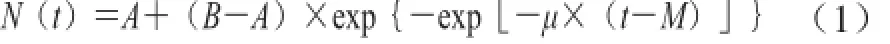
式中：N（t）是t時的微生物數量（lg（CFU/g））；A是當時間無限趨近于零時的漸進對數值（相當于初始微生物數量）（lg（CFU/g））；B是達到穩定期時達到的最大微生物數量（lg（CFU/g））；μ是在t = M時的相對最大生長速率/d-1；M是達到相對最大生長速率所需要時間/d。

根據以下公式，計算初始微生物數量N0，最大微生物數量Nmax，最大比生長速率μmax與遲滯時間λ：

式中：μmax是最大比生長速率/d-1；e = 2.718 2；λ是遲滯時間/d。

1.5.2 修正的Logistic模型

修正的Logistic模型表達式為[10]：

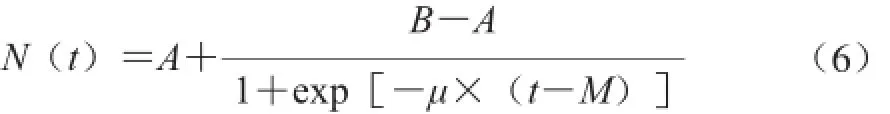
式中：N（t）是t時的微生物數量（lg（CFU/g））；A是當時間無限趨近于零時的漸進對數值（相當于初始微生物數量）（lg（CFU/g））；B是達到穩定期時達到的最大微生物數量（lg（CFU/g））；μ是在t = M時的相對最大生長速率/d-1；M是達到相對最大生長速率所需要的時間/d。

根據以下公式，計算初始微生物數量N0，最大微生物數量Nmax，最大比生長速率μmax與遲滯時間λ：

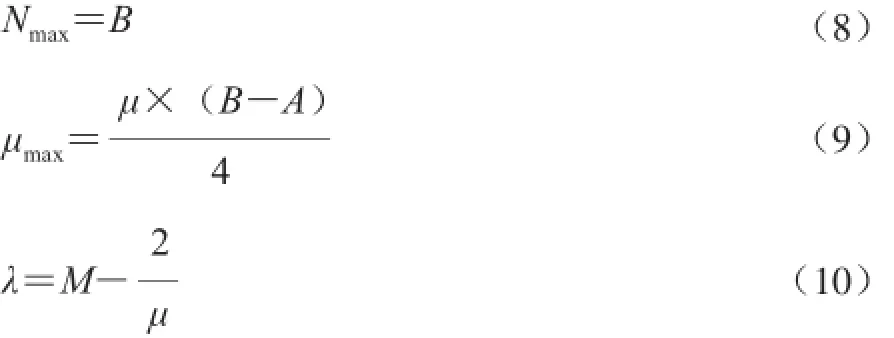
式中：μmax是最大比生長速率/d-1；λ是遲滯時間/d。

1.5.3 Baranyi模型

Baranyi模型屬于理論模型，是英國食品與環境研究院（the Food and Environment Research Agency，FERA）開發的Growth Predictor的基礎模型，其函數表達式[11]為：

式中：N（t）是t時的微生物數量（lg（CFU/g））；N0是t = 0時的初始微生物數量（lg（CFU/g））；Nmax是穩定期時達到的最大微生物數量（lg（CFU/g））；μmax為微生物生長的最大比生長速率/d-1；d0是最大比生長速率μmax與遲滯時間λ的乘積；t是時間/d。

1.6 二級模型的擬合

二級模型主要描述溫度等因素對微生物生長動力學參數的影響。

1.6.1 Arrhenius模型

Arrhenius模型[12]表達式如下：

式中：aμ是常數；Ea是活化能；R = 8.314 J /（mol·K）；T是開氏溫度/K。

1.6.2 平方根模型

平方根模型[13]表達式如下：

式中：T是貯藏溫度/℃；Tminμ為假設概念，指理論上微生物細胞能夠代謝的最低溫度/℃；bμ是回歸直線的斜率/（（d-1）1/2/℃）。

1.7 以比較參數進行的模型評價

使用均方誤差平方根RMSE、回歸系數R2[5,14-15]、赤池信息準則（AIC）與貝葉斯信息準則（BIC）[3]評價模型的擬合優度，以比較不同模型的擬合效果。其中RMSE、AIC與BIC值越小說明擬合優度越高，R2則是越接近1擬合優度越高。各參數表達式如下：

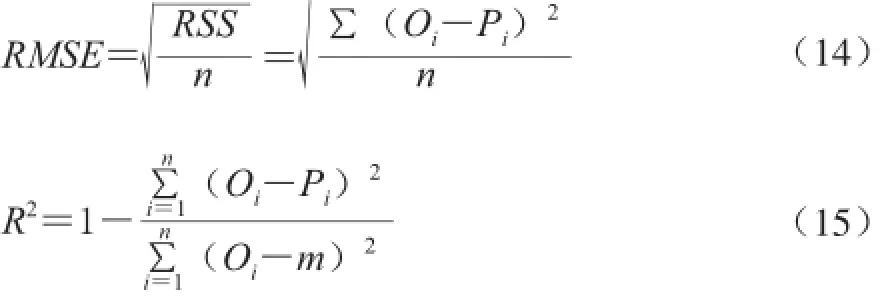
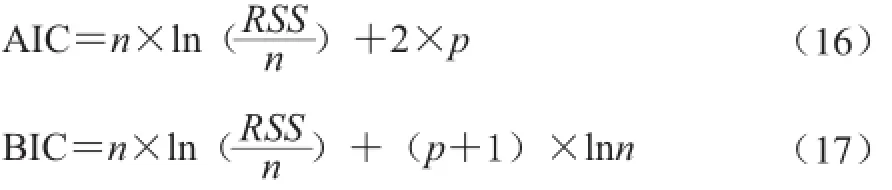
式中：RSS是殘差平方和；n是數據點數量；Oi是第i個數據點的實測觀察值；Pi是第i個數據點的預測值；m是平均值；p是模型的特征值數量，即自變量個數。

1.8 以比較貨架期進行的模型評價

通過比較表達式（18）所計算的預測值貨架期（shelf life，SL）與實測值（最小腐敗量N（t）=6.5（lg（CFU/g））時的t值）的殘差值，可得出貨架期預測模型的準確度。由于以不同的一級模型為基礎所計算的實測值與預測值均不同，所預測的貨架期準確度有所差異，可據此比較各一級模型的擬合優度。

在生長動力學模型的基礎上，SL以初始菌數增加到最小腐敗量所需要的時間來預測[18]。模型表達式如下：

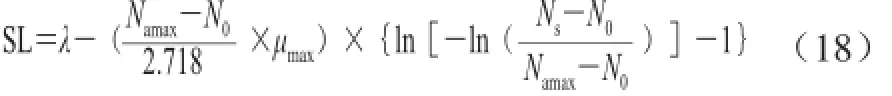
式中：SL是貨架期/d；Namax是各溫度下樣品最大菌數的平均值（lg（CFU/g））；Ns為最小腐敗量菌數（lg（CFU/g））。

2 結果與分析

2.1 一級模型的比較

表1 使用不同一級模型擬合所得特征值的比較Table 1 Eigenvalue comparison of the different primary models used for fitting the experimental data

表1是使用修正的Gompertz模型（mGM）、修正的Logistic模型（mLM）與Baranyi模型（BM）對實驗數據進行擬合所得的特征值。其中，mLM所得N0值的平均值（1.851 7（lg（CFU/g）））明顯小于mGM與BM（P＜0.05），并且與實測值（2.371 1（lg（CFU/g）））相差較大；3 個模型所得Nmax值的平均值無顯著差異（P＞0.05）。

由表1可知，在不同溫度下，mGM與mLM所得最大比生長速率μmax較為接近，均小于BM，這是由于在描述微生物生長由延滯期進入對數期的變化時，mGM與mLM函數的拐點較平滑，計算所得對數期初始生長速率偏大，導致最大比生長速率μmax偏小。不同模型所得延滯時間λ的數值差異較大，其中mLM將15 ℃貯藏組所得的延滯時間計算為負值，但微生物生長的延滯期λ不可能為負值，由此得出使用mLM擬合失敗。

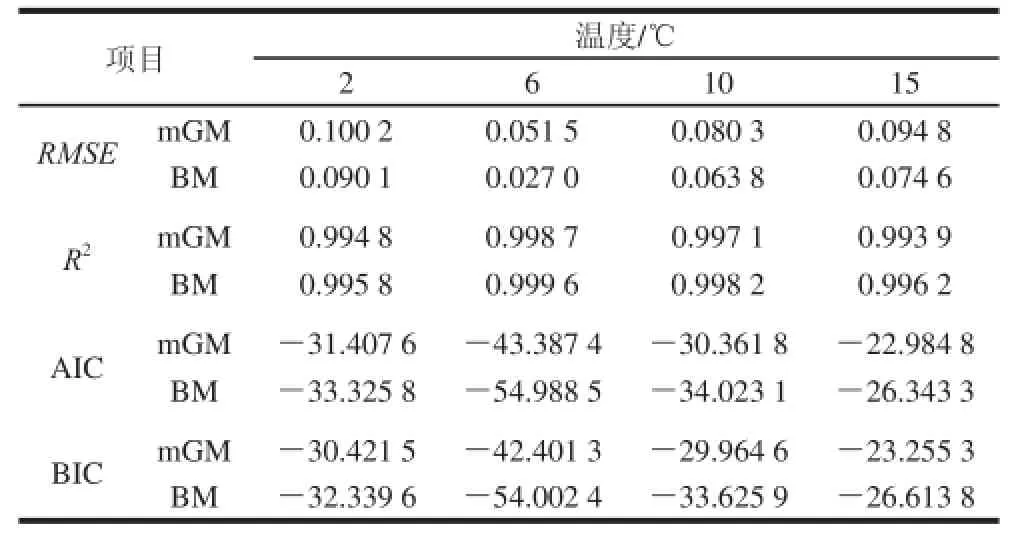
表2 不同一級模型擬合結果評價參數的比較Table 2 Statistical indices comparison of the different primary models used for fitting the experimental data

由表2可知，對于所有貯藏組，與mGM相比，BM所得方程的RMSE值均較小，R2值更接近于1，而且BIC、AIC值均較小，結合參數屬性能夠說明，在這3 種一級模型中，BM所得方程的評價參數較優，即擬合優度較高。

2.2 二級模型的比較

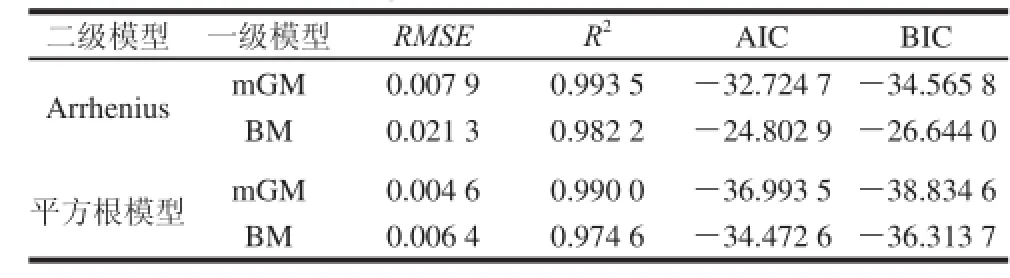
表3 不同二級模型擬合結果的評價參數Table 3 Statistical indices of the different secondary models used for fitting the experimental data

表3是使用2 種二級模型，針對不同一級模型擬合所得的統計學數據。Arrhenius模型與平方根模型均擬合成功。與平方根模型相比，Arrhenius模型擬合所得R2值更接近1，但RMSE值較小，而AIC值與BIC值的差異較小，無法得出哪個模型擬合優度更高。

由表3還可知，相較于BM，二級模型擬合時使用來自mGM的生長數據所得的R2稍接近1，RMSE值稍小，AIC與BIC值亦較小，說明這3 種一級模型中，應用mGM對優化特定二級模型（Arrhenius及平方根模型）的評價參數比較有利。

2.3 以比較貨架期進行的模型評價

表4 使用不同模型所得雞肉早餐腸貨架期Table 4 Shelf life (SL) of breakfast chicken sausage in days estimated by using different models

由表4可知，BM所得殘差值均在1 d左右，而mGM在6 ℃條件下的殘差值超過2 d，說明用于估測本產品貨架期時，BM優于mGM。

3 討 論

微生物生長曲線形狀與模型幾何特征均對擬合優度有影響[16]，Baranyi方程包含四部分：常數項、線性函數、指數函數及對數函數；Gompertz模型與Logistic模型均為S型曲線，分為漸增期、快增期與緩增期[17]。這使得擬合所得的特征值有所差異。

本實驗對于真空包裝雞肉早餐腸貯藏期間細菌總數變化的數學模型建立進行了研究，經分析后認為一級模型中Baranyi模型擬合優度最高，其次為修正的Gompertz模型，最后為修正的Logistic模型；二級模型中Arrhenius模型與平方根模型均能夠成功擬合。目前已有的研究結果中對Baranyi模型及Gompertz模型的比較結論存在差異，而Logistic模型則被普遍認為次優。其中Slongo等[4]比較了修正的Gompertz模型與修正的Logistic模型的擬合結果，認為前者擬合優度更高；Juneja等[5]使用幾種不同模型擬合沙門氏菌在雞肉貯藏中的變化情況，結果表明Baranyi模型擬合優度高于修正的Gompertz模型與Logistic模型；Xiong等[18]認為Baranyi模型比修正的Gompertz模型擬合優度高，擬合結果更穩定；這些報道均與本實驗研究結論相同，可能原因是Gompertz模型的S型曲線中不存在線性線段，但微生物的對數期變化軌跡呈現較好的線性，且S型曲線中的漸增期與微生物實際生長中存在的延滯期不符，出現了延滯期較短的對象。而Baranyi[5,11,19]方程以微生物生長的微分方程dM/dt = μM作為基礎模型，即是在理解了微生物生長規律后建立的，能夠從數學角度克服Gompertz模型存在的缺陷。但是，Mataragas等[2]對熟制肉中特定腐敗菌的生長情況進行擬合，認為修正的Gompertz模型擬合優度高于Baranyi模型及修正的Logistic模型，與本實驗結果不一致，這可能與微生物種群、環境及食品基質條件的差異有關[20]。

4 結 論

針對真空包裝雞肉早餐腸貯藏期的微生物生長狀況，以評價參數（RMSE、R2、AIC、BIC）為主要參考值，特征值及貨架期殘差值為輔助參考值，對不同預測模型的擬合優度進行了比較。其中Baranyi模型所得方程的評價參數最優，最大比生長速率μmax最大，所得產品貨架期殘差值較小；應用修正的Gompertz模型更有利于優化二級模型評價參數；而修正的Logistic模型擬合所得初始菌數N0值偏小，且將15 ℃貯藏組延滯時間λ計算為負值。因此Baranyi模型擬合優度最高，其次為修正的Gompertz模型，修正的Logistic模型擬合優度最低，與大多已知研究結論一致。但Arrhenius模型與平方根模型均能夠成功擬合，未得出擬合優度更高者。

[1] BUCHANAN R L. Predictive food microbiology[J]. Trends in Food Science & Technology, 1993, 4(1): 6-11.

[2] MATARAGAS M, DROSINOS E H, VAIDANIS A, et al. Development of a predictive model for spoilage of cooked cured meat products and its validation under constant and dynamic temperature[J]. Food Microbiology and Safety, 2006, 71(6): 157-167.

[3] QUINN G P, KEOUGH M J, 蔣志剛, 等. 生物實驗設計與數據分析[M].北京: 高等教育出版社, 2003: 144-145.

[4] SLONGO A P, ROSENTHAL A, CAMARGO L M Q, et al. Modeling the growth of lactic acid bacteria in sliced ham processed by high hydrostatic pressure[J]. Food Science and Technology, 2009, 42(1): 303-306.

[5] JUNEJA V K, MELENDRESB M V, HUANG Lihan, et al. Modeling the effect of temperature on growth of Salmonella in chicken[J]. Food Microbiology, 2007, 24(4): 328-335.

[6] 張海波, 段修軍, 張依裕, 等.白羽番鴨生長曲線擬合比較分析[J]. 中國畜牧獸醫, 2009, 36(2): 148-151.

[7] 朱志明, 強巴央宗, 朱猛進, 等. 藏雞生長曲線擬合和分析的比較研究[J]. 中國農業科學, 2005, 39(10): 2159-2162.

[8] 張浩, 吳常信, 李俊英, 等. 藏雞和低地雞種的生長曲線擬合與雜種優勢分析[J]. 中國畜牧雜志, 2005, 41(5): 34-37.

[9] 戴國俊, 王金玉, 王志躍, 等. 新揚州雞不同環境體重體尺生長曲線擬合研究[J]. 浙江農業學報, 2005, 17(6): 372-375.

[10] GIBSON A M, BRATCHELL N, ROBERTS T A. The effect of sodium chloride and temperature on rate and extent of growth of Clostridium botulinum type a in pasteurized pork slurry[J]. Journal of Applied Bacteriology, 1987, 62(6): 479-490.

[11] BARANYI J, ROBERTS T A. A dynamic approach to predicting bacterial growth in food[J]. International Journal of Food Microbiology, 1994, 23(3/4): 277-294.

[12] DAVEY K R. Applicability of the Davey (linear Arrhenius) predictive model to the lag phase of microbial growth[J]. Journal of Applied Bacteriology, 1991, 70(3): 253-257.

[13] RATKOWSKY D A, OLLEY J, MCMEEKIN T A, et al. Relationship between temperature and growth rate of bacterial cultures[J]. Journal of Bacteriology, 1982, 149(1): 1-5.

[14] CAYRé M E, VIGNOLO G, GARRO O. Modeling lactic acid bacteria growth in vacuum-packaged cooked meatemulsions stored at three temperatures[J]. Food Microbiology, 2003, 20(5): 561-566.

[15] ROSS T. Indices for performance evaluation of predictive models in food microbiology[J]. Journal of Applied Bacteriology, 1996, 81(5): 501-508.

[16] 李柏林, 郭劍飛, 歐杰. 預測微生物學數學建模的方法構建[J]. 食品科學, 2004, 25(11): 52-57.

[17] 崔黨群. Logistic 曲線方程的解析與擬合優度測驗[J]. 數理統計與管理, 2005, 24(1): 112-115.

[18] XIONG R, XIE G, EDMONDSON A S, et al. Comparison of the Baranyi model with the modified Gompertz equation for modeling thermal inactivation of listeria monocytogenes Scott A[J]. Food Microbiology, 1999, 16(3): 269-279.

[19] HUANG Lihan. Growth kinetics of Escherichia coli O157:H7 in mechanically-tenderized beef[J]. International Journal of Food Microbiology, 2010, 140(1): 40-48.

[20] 劉超群, 王宏勛, 侯溫甫. 低溫肉制品微生物控制與預測模型應用研究進展[J]. 食品科學, 2009, 30(21): 481-484.

Goodness-of-Fit Comparison of Growth Models for the Total Bacterial Count in Vacuum-Packaged Chicken Breakfast Sausage

CHEN Rui, XU Xing-lian*, ZHOU Guang-hong, WANG Peng
(Key Laboratory of Meat Processing and Quality Control, Ministry of Education, Nanjing Agricultural University, Nanjing 210095, China)

In order to compare the goodness-of-fit of growth models for the total bacterial count in vacuum-packaged chicken breakfast sausage, the primary models Baranyi, modified Gompertz and modified Logistic, and the secondary models Arrhenius and square root equations were chosen for conducting following studies, respectively. They were compared by calculating their indices (such as root mean square error (RMSE), R2, Akaike information criterion and Bayesian information criterion), and the characteristic values and residuals of the shelf life model. Results showed that the Baranyi model exhibited the best performance indices and the highest maximum specific growth rate (μmax) and provided smaller shelf life residuals, while the modified Gompertz model was better in optimizing the secondary model and the modified Logistic model presented the wrong characteristic values. Thus the goodness-of-fit of the Baranyi model was the best, followed by the modified Gompertz model, and the modified Logistic model showed the worst goodness-of-fit. The comparison of Arrhenius equation and square root equation did not draw a conclusion.

prediction model; goodness-of-fit; temperature; comparison

TS251.55

A

1002-6630（2014）15-0113-05

10.7506/spkx1002-6630-201415023

2013-07-17

江蘇省科技成果轉化專項資金項目（BA2009007）；“十二五”農村領域國家科技計劃子課題（2012BAD28B01-03）

陳睿（1990—），女，碩士研究生，研究方向為肉品質量安全控制。E-mail：yuxin_90214@yahoo.com.cn

*通信作者：徐幸蓮（1962—），女，教授，博士，研究方向為肉品質量控制。E-mail：xlxu@njau.edu.cn