x-11-ARIMA過程在痢疾疫情預測中的應用研究*

申銅倩劉文東胡建利朱葉飛鮑昌俊湯奮揚彭志行陳 峰Δ

x-11-ARIMA過程在痢疾疫情預測中的應用研究*

申銅倩1劉文東2胡建利2朱葉飛2鮑昌俊2湯奮揚2彭志行1陳 峰1Δ

目的探尋江蘇省痢疾疫情的季節分布規律，為及時采取預防措施提供理論依據。方法應用x-11-ARIMA過程分析江蘇省2000年至2012年的痢疾月度數據，采用SAS軟件將時間序列數據拆分成長期趨勢起伏T，季節波動S，不規則波動I三個部分。結果痢疾發病帶有一定季節性，每年重復進行，趨勢大體相同；每年的7、8月份為痢疾高發期，12月至次年的3月份處于發病低谷期；2000-2005年季節因子波動振幅較大，而后隨時間推移有減弱的趨勢。結論痢疾的發生比較穩定，x-11-ARIMA模型分析其季節分布規律有較好的科學性和實用性。

時間序列 x-11-ARIMA 季節分布 預防與控制

痢疾是《中華人民共和國傳染病防治法》中規定的乙類傳染病，是一種常見的急性腸道傳染病，多發于兒童和老人，嚴重影響居民健康和生活質量。研究痢疾的發病規律，對痢疾的疫情進行預測和分析，可以為痢疾的預防控制、資源配置提供科學依據。

痢疾發病人數的時間序列（time series）中通常包含大量的信息，是建模和預測的主要依據。痢疾的發病比較穩定，有規律可循，運用時間序列分析的方法，可以做出比較準確的預測。本文采用x-11-ARIMA過程對2000-2011年的數據進行分析，提取季節因子，趨勢循環因子，尋找痢疾的發生發展規律，服務于痢疾的防治工作。

資料與方法

1.資料來源

從江蘇省傳染病疫情網絡直報系統收集到2000年1月至2012年10月的痢疾病例數，由于江蘇省人口基數較大，且比較穩定，故選擇痢疾月發病數代替發病率來反映疾病的流行情況。

2.模型簡介

（1）x-11過程

x-11過程是美國國情調查局編制的時間序列季節調整過程。它的基本原理就是時間序列的確定性因素分解方法。x-11過程基于這樣的假定：任何時間序列都可以拆分成長期趨勢起伏（T），季節波動（S），不規則波動（I）和交易日影響（D）［1］。因此任何一個時間序列都可以如下分解：

乘法模型：xt＝Tt·St·Dt·It

加法模型：xt＝Tt＋St＋Dt＋It

x-11方法是基于移動平均法的季節調整方法，是通過幾次迭代來分解的時間序列的季節因子、趨勢循環因子和不規則因子等各因子成分，每一次對各組成因子的估算都進一步精化［2］。

x-11方法用一系列中心化滑動平均來估計季節成分，這些滑動平均對除起始和結尾處的所有觀測使用對稱權重，但起始處和結尾處只能用非對稱權重。非對稱權重可以導致季節因子估計不準，因而，有了新數據以后就可能造成大的更改。這種很大的更改并不常見，但這種情況還是有可能發生的，發生了這種情況就會降低x-11方法的可信度。

加拿大統計局開發了一種方法來處理這個問題。該方法稱為x-11-ARIMA方法，它先把原始序列（如需預調整先做預調整）用ARIMA模型預報一年或幾年，然后把這個延長了的序列進行季節調整，只不過這時在序列的原尾部用的就是對稱權重了，這種方法已經用大量加拿大經濟序列進行了測試，它確實能大大減少新數據加入時對序列的更改［3］。

（2）ARIMA模型

ARIMA（autoregressive intergrated moving average）是Box-Jenkins方法中的重要的時間序列分析預測模型，又稱為自回歸求和移動平均模型。它是將預測對象隨時間推移而形成的時間序列視為一個隨機序列，即除去個別的因偶然因素引起的觀測值外，時間序列是一組依賴于時間t的隨機變量。這組隨機變量所具有的依存關系或自相關性表征了預測對象發展的延續性，而這種自相關性一旦被相應的數學模型描述出來，即可以用時間序列的過去和現在觀測值預測未來，ARIMA方法以時間序列的自相關分析為基礎，對時間序列求其本身與不同滯后期的一系列自相關函數（autocorrelation function ACF）和偏自相關函數（partial autocorrelation function PACF），以此識別時間序列的特性。根據參數選擇的不同，模型可分為：ARIMA（p，d，q），ARMA（p，q），AR（p）和MA（q）［4］。建立ARIMA模型可歸納為4個具體步驟：數據的預處理（平穩化）；模型的識別、定階與模型的參數估計；模型的診斷檢驗［5-6］；序列預測。

本文采用x-11-ARIMA模型對此時間序列數據進行分析。其步驟是，先對原始序列（如需調整先做調整）用ARIMA模型預報一年，然后把這個延長了的序列運用x-11過程進行季節調整。

結 果

1.ARIMA模型

本文采用2000.01-2011.12的數據建立ARIMA模型，用2012年的數據進行預測，評價預測精度。

（1）原始序列

將每年痢疾病例數隨時間變化趨勢繪成圖［7］，可見每年痢疾發病趨勢大體相同，從1月份開始逐漸增多，7、8月份達到頂峰，而后逐漸減少。發現痢疾發病是有周期性的，且逐年減少，2004年尤其多；

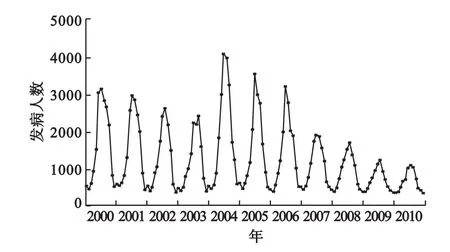
圖1 痢疾按月發病數序列時序圖

（2）數據預處理

痢疾發病存在趨勢性和明顯的周期性，為了使序列平穩化，對發病人數取對數值，然后采用一階差分來消除趨勢性，12步差分來消除季節性，差分后序列圖見圖2。對處理后的序列進行ADF檢驗，P＜0.001，說明序列已經平穩化。

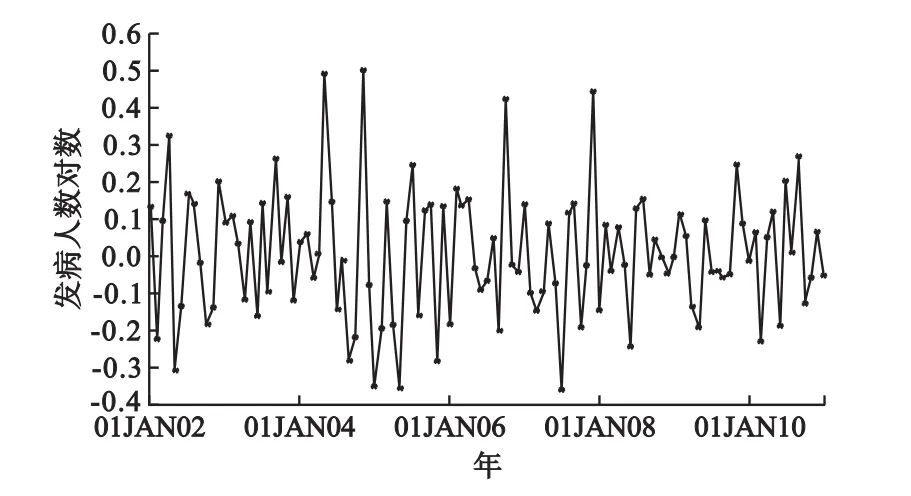
圖2 差分后痢疾發病數序列對數圖

（3）模型的識別、定階與參數估計

對ARIMA模型的階數識別及參數估計，立足于考察數據的樣本自相關、偏自相關函數［5］。由圖3可見，季節波動已經消除。在模型識別階段，我們采用1逐期差分和季節差分來消除趨勢性和季節性，故d＝1，D＝1，選用乘積季節模型（p，d，q）×（P，D，Q）S。

圖3 自相關、偏自相關函數圖

（4）參數估計與模型檢驗

SAS軟件自動選擇最優模型，方程為：

（1-B）（1＋0.36B12）lncaset＝（1-0.31B-0.23B2）（1-B12）εt

建立預測模型后，對其進行殘差自相關性檢驗，延遲各階LB統計量的P值均顯著大于α（α＝0.05），所以模型擬合成立，見表1。

（5）序列預測

模型擬合好之后，可以進行短期預測。我們采用此模型對2012.01-2012.10痢疾發病數進行預測，并對其預測精度做出評價［5］，見表2。

表1 序列白噪聲檢驗

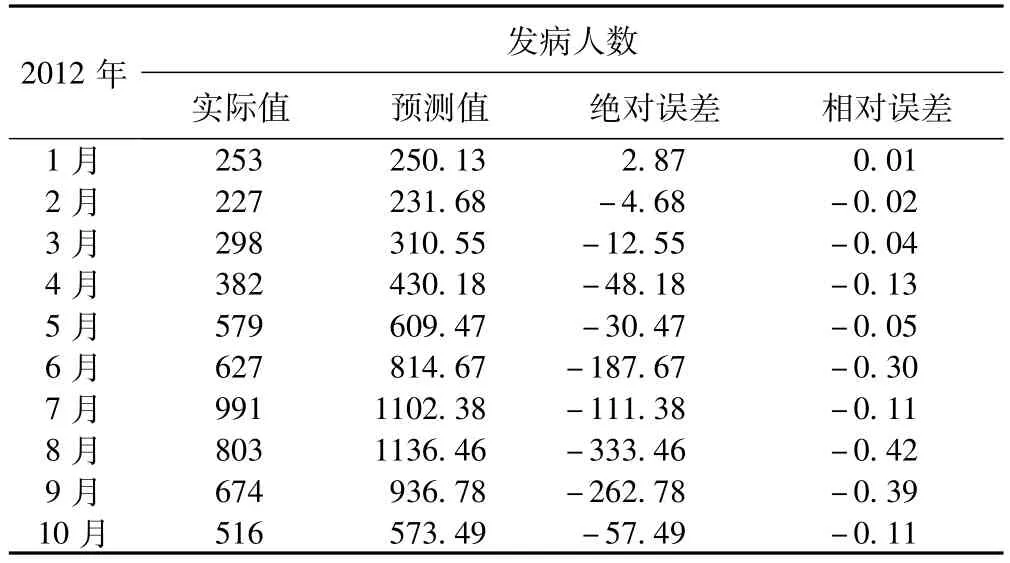
表2 ARIMA模型對2012年1月至10月江蘇省痢疾發病情況預測結果

（6）繪制擬合預測圖

圖4中，*表示觀測數據，曲線是根據預測值繪制而成以及95%可信區間。

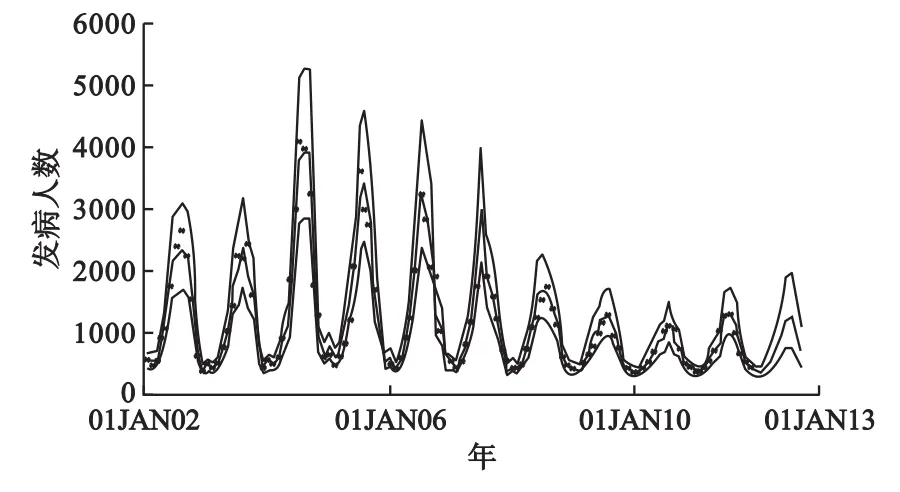
圖4 預測曲線及95%可信區間

2.x-11-ARIMA模型

x-11-ARIMA模型默認延長1年的數據，對延長后的序列（2000.01-2012.10）運用x-11過程進行季節調整。

（1）季節因子

以時間為橫坐標，以季節因子為縱坐標，將各時點數據繪成圖5，從圖5可以看出痢疾發病的季節分布特征，以及季節因子隨時間的推移而發生的變化。季節因子在12月到次年的3月較低，7月、8月最高；2000-2005年季節波動振幅較大，并隨時間的推移逐漸減小。

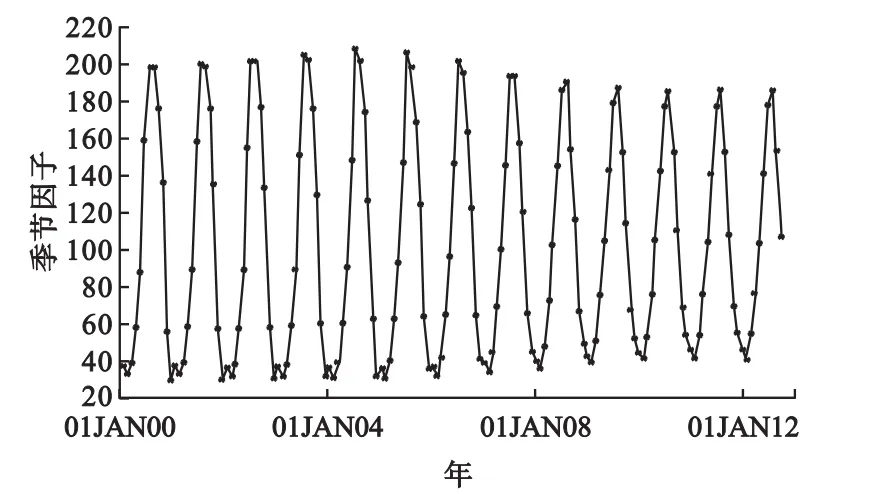
圖5 痢疾發病數時間序列季節因子

（2）趨勢循環

趨勢循環是從時間序列中過濾掉季節因子和不規則成分，將時間序列的長期變化趨勢暴露出來，趨勢循環包含了長期趨勢和周期循環。以時間為橫坐標，以趨勢循環因子為縱坐標，將各時點數據繪成圖6。痢疾的發病人數是以1年為周期性上下波動的，總體趨勢是下降的，2004年急劇上升達到頂峰，而后逐年下降達到近乎穩定狀態。

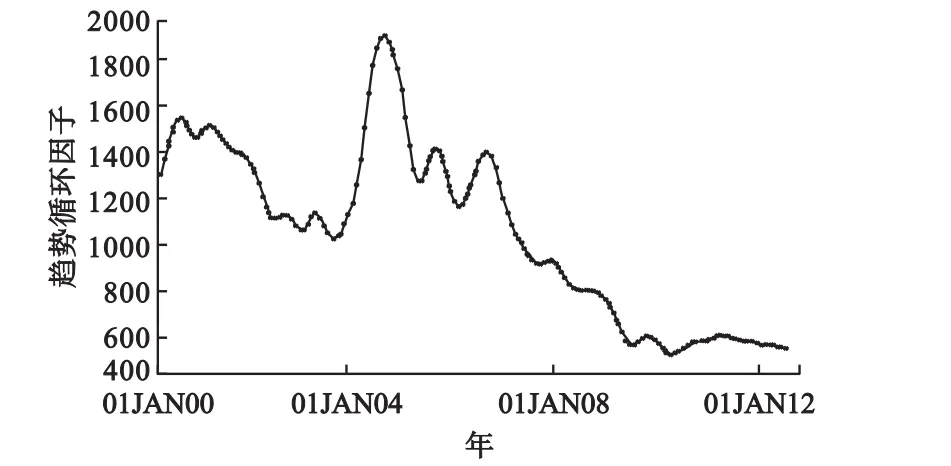
圖6 痢疾發病數時間序列趨勢循環因子

（3）不規則波動

時間序列的季節因子、周期趨勢起伏因子分離出來后，剩下的是不規則成分，包括各種因偶然因素所導致的痢疾發病人數的波動，見圖7。

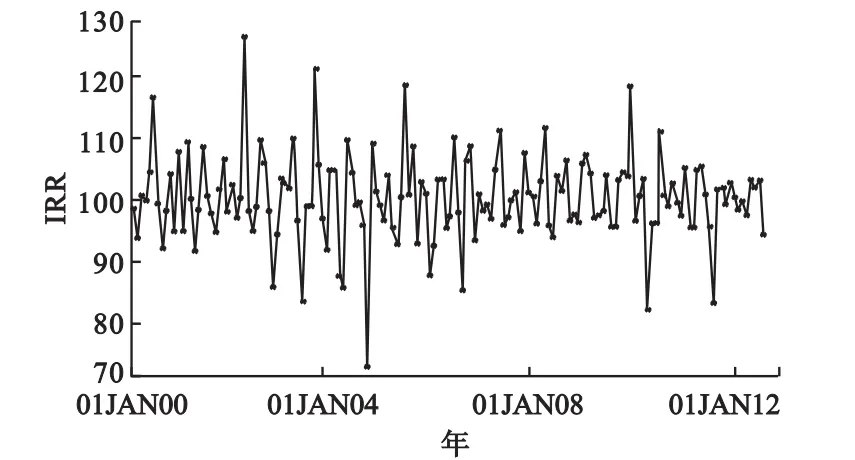
圖7 痢疾發病數時間序列不規則因子

討 論

痢疾是一種常見的急性腸道傳染病，是一個重大公共衛生問題，嚴重影響居民健康和生活質量。對痢疾發病情況的預測預報研究是公共衛生領域研究的重要課題之一。傳統的時間序列模型要求序列具有平穩的線性趨勢，但實際上痢疾的發病情況有著明顯的季節性和周期性，如果不考慮這些因素的影響，做出的預測往往不準確［5］。本文采用x-11-ARIMA模型來揭示痢疾多發于夏秋季節，其中7、8月份最高發，12月至次年的3月為低發期。其發病可能與氣候息息相關，溫度越高，越潮濕，越溫和的條件，越有利于疾病的發生。其中溫度是最主要的影響因素，它直接影響到病原體的繁殖速度和存活；另外氣候的變化會影響到人們的生活方式，比如飲食習慣，從而間接地對疾病的傳播起到一定的作用［8］。識別疾病的高發期，以便當地政府及時采取預防措施是很有必要的。

有文獻報道，痢疾多發于人口密度大但衛生設施不健全的地方［9］。2000年到2005年季節因子波動振幅較大，而后逐年減小也說明隨著國家經濟文化的發展、衛生條件的改善、政府對痢疾的預防和控制力度的加強以及人們對其發病情況預測的水平不斷提高，近年來痢疾的發病率總體上呈現一定的下降趨勢。既SARS之后，傳染病得到極大的重視，疫情直報系統逐步完善，國家投入大量資金開展傳染病的監測與防治工作。2004年痢疾發病人數呈現急劇增加，達到頂峰，之后逐年下降，基本達到穩定狀態。本文的預測結果與實際情況相吻合。

x-11過程產生漸變的季節成分，允許每年的季節效應各不相同，而季節指數法、指數平滑法、趨勢季節模型等方法只能計算得到唯一固定的季節成分，不如x-11過程靈活和接近實際情況。x-11方法沒有建立模型，不進行參數估計，也不用于預測，只是將各種因子分離開來。x-11-ARIMA是先對原始序列（如需調整先做調整）用ARIMA模型預報一年，然后把這個延長了的序列運用x-11過程進行季節調整，它充分結合了x-11與ARIMA模型的優點，使分析結果更可靠。

痢疾的發病原因比較復雜，是人類與環境綜合作用的結果，如：貧窮、水資源、氣候［10］。目前由于抗生素的濫用，缺少疫苗及有效的治療措施等原因，痢疾仍是危害人類的一大疾病。衛生統計工作與疾病預防控制工作相結合，做出可靠的預測，為疾病的預防控制提供依據是我們將來的工作方向。由于報告日期晚于發病日期，所以可能存在滯后現象。采用周數據可能會比月度數據預測結果更準確［8］。本文痢疾發病人數來源于江蘇省傳染病疫情直報系統，是報告病例數，為了避免報告偏倚的存在，數據收集的準確性與完整性也是我們努力的方向。

1.王燕主編.應用時間序列分析，第2版.北京：中國人民大學出版社，2008.

2.孫奕，覃世龍，嚴春香，等.X-11季節調整方法在醫院時間序列分析中的應用.中國衛生統計，2007，24（1）：71-73.

3.SAS Institute Inc..SAS/ETS（R）9.2 User′s Guide.USA：2007.

4.朱猛，祖榮強，霍翔，等.時間序列分析在流感情預測預警中的應用.中華預防醫學雜志，2011，45（12）：1108-1111.

5.彭志行，陶紅，賈成梅，等.時間序列分析在麻疹疫情預測預警中的應用研究.中國衛生統計，2010，27（5）：459-463.

6.Peter J.Brockwell and Richard A.Davis著，田錚譯.時間序列的理論與方法，第2版.北京：高等教育出版社，2001.

7.Quantitative M icro Software LLC.Eviews5 User′s Guide.USA：2004.

8.Zhang Ying，Bi Peng，Janet E.Hiller，et al.Weather and the Transm ission of Bacillary Dysentery in Jinan，Northern China：A Time-Series A-nalysis.Public Health Rep，2008，123（1）：61-66.

9.Guan P，Huang DS，Guo JQ，et al.Bacillary Dysentery Meteorological Factors in Northeastern China：a Historical Review Based on Classification Regression Trees.Jpn J Infect Dis，2008，61（5）：356-360.

10.Kelly-Hope Louise A，Alonso W ladim ir J，Thiem Vu Dinh，et al.Temporal Trends and Climatic Factors Associated w ith Bacterial Enteric Diseases in Vietnam.Environmental Health Perspectives，2008，116（1）：7-12.

（責任編輯：劉 壯）

The Application of x-11-ARIMA Process in Dysentery Prediction

Shen Tongqian，Liu Wendong，Hu Jianli，et al（DepartmentofEpidemiology＆Biostatistics，SchoolofPublicHealth，Nanjing MedicalUniversity（210029），Nanjing）

ObjectiveTo explore the seasonal distribution of dysentery in Jiangsu province，and provide a theoretical basis for disease prevention and control.MethodsThemonthly data between January 2000 to October2012 is collected，and we apply x-11-ARIMA to extract secular trend，seasonal fluctuation and irregular fluctuation from the distribution of dysentery.ResultsDysentery distributes w ith a season rule，and the trend is generally same every year.July and August is the peak，and the incidence is low during December to the follow ing 3 months.The season factor fluctuation amplitude is bigger in 2000-2005，then it has a dim inished trend over time.Conclusionthe distribution of dysentery is stable，and it is scientific and practical to apply x-11-ARIMA to analyze seasonal rule of dysentery.

Time series analysis；x-11-ARIMA；Seasonal distribution；Prevention and control

*：“十二五”國家科技重大專項（2011ZX10004-902），江蘇省自然科學基金重點項目（BK2010079），江蘇省科教興衛工程（ZX201109），江蘇省高校優勢學科建設資助項目

1.南京醫科大學公共衛生學院流行病與衛生統計學系（210029）

2.江蘇省疾病預防與控制中心

△通信作者：陳峰，E-mail：fengchen＠njmu.edu.cn