Cox比例風險Frailty模型簡介與軟件實現*

朱 玉梅 楊李 杰陳佰鋒姚應水△

Cox比例風險Frailty模型簡介與軟件實現*

朱 玉1梅 楊2李 杰1陳佰鋒1姚應水1△

目的介紹Cox比例風險Frailty模型的原理及其在SAS 9.3軟件中的實現過程。方法利用具體數據的分析過程介紹Cox比例風險Frailty模型在SAS 9.3軟件中的實現，并比較Cox比例風險模型與Cox比例風險Frailty模型的分析效果。結果Frailty項對數變換后的方差估計值為0.831，與0比較差異有統計學意義，有必要在Cox比例風險模型中加入Frailty項。結論Cox比例風險Frailty模型能夠揭示資料的異質性，準確地分析因素對結局變量的影響，獲得更為客觀的分析結論。

Frailty模型 Cox比例風險模型 Cox比例風險Frailty模型

以時間到事件（Time-To-Event）為結局變量的生存分析方法眾多，其中經典的分析方法是Cox比例風險模型。它的理論假設之一是研究對象間相互獨立，即研究對象間具有同質性，這暗示每個研究對象有相同的基線風險。在實際研究中，這種假設不易達到，由于未知因素或設計等原因，導致研究對象個體間或組別間存在異質性，研究對象表現出組內相關的特性，經典的生存分析不再適合分析這類型的數據。這時，需要對經典的生存分析的方法進行改進，引入Frailty項（異質性變量），發展為Frailty模型（異質性模型）。本文介紹加入Frailty項的Cox比例風險模型——Cox比例風險Frailty模型和軟件實現。

基本原理

以多中心臨床隨機化對照試驗為例，介紹Cox比例風險Frailty模型。中心i（i＝1，2，…，k），每個中心的研究對象j（j＝1，2，…，ni）。在介紹Cox比例風險Frailty模型之前，先回顧下Cox比例風險模型。

1.Cox比例風險模型

Cox提出比例風險模型［1］如下：

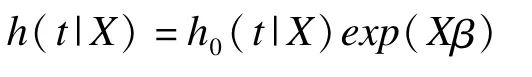
其中h0（t｜X）稱為基線風險函數，h（t｜X）表示在協變量為X條件下的風險函數，exp（β）為風險比（hazard ratio，HR）。Cox比例風險模型最突出的優點在于，對參數β的估計并不依賴于基線風險函數的取值。但是，它要求研究對象相互獨立，即研究對象具有同質性。

2.Cox比例風險Frailty模型

當分析多中心臨床隨機化對照試驗的數據時，每個中心的基線風險可能不一致，需要對Cox比例風險模型進行如下改進，發展為Cox比例風險Frailty模型［2-7］，如下：

其中γi為中心i（i＝1，2，…，k）的隨機效應，其它同Cox比例風險模型。常對γi做如下假設：

上式改寫為下式：

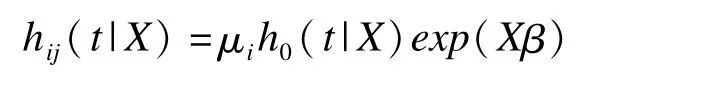
其中μi被稱為Frailty項（異質性變量），μi是相互獨立同分布的，其期望是1，方差為未知參數θ2，通常還假設其與X相互獨立，當μi＝1時Cox比例風險Frailty模型蛻變為Cox比例風險模型。此外，Elbers和Ridder［8］證明了在Frailty項的期望為1的條件下，模型是可估的。

當μi＞1時說明中心i內的研究對象傾向于加速失效（事件發生）；當μi＜1時說明中心i內的研究對象傾向于減速失效（事件發生）；當μi＝1時說明中心i內的研究對象的失效風險（事件發生）是正常風險。

為了估計未知參數，需要對Frailty項的分布做出假設。原則上期望為1和具有有限方差的任一正連續分布都可以作為Frailty項的分布。在應用中常采用的分布有伽馬分布、逆高斯分布和對數正態分布等。方差θ2的估計方法有限制性最大似然估計（residual maximum likelihood，REML）和最大似然估計（maximum likelihood，ML）。

實例分析與軟件實現

下面結合SASPROC PHREG過程和SAS help中提供的數據介紹Cox比例風險Frailty模型的應用和軟件實現［7］。

1.數據簡介

該數據來源于一項關于糖尿病患者眼睛失明的研究，共包含197例糖尿病患者，他們的眼睛有很高的失明風險，每個研究對象的兩只眼睛中隨機選擇一只眼睛接受激光光凝治療，研究的目的主要是探索激光光凝治療有沒有延緩眼睛失明的進程。因為青少年和成年糖尿病有不同的發展過程，所以同時檢查發病年齡和眼睛失明時間有無關聯。每個患者是一個“群（clusters）”，類似于上文提到的“中心”，因為左右眼睛沒有生物學差異，我們假設它們有相同的基線風險。變量（id）表示患者編號，變量（time）是患者眼睛失明時間，變量（status）表示眼睛失明狀況（是二分類變量，“0”代表沒有失明，“1”代表失明），變量（age）表示患者的發病年齡（是二分類變量，“0”代表發病年齡≤20，“1”代表發病年齡＞20），變量（treatment）表示眼睛接受治療的方法（是二分類變量，“0”代表其他治療，“1”代表激光光凝治療）。用數據步建立數據集blind，見表1。

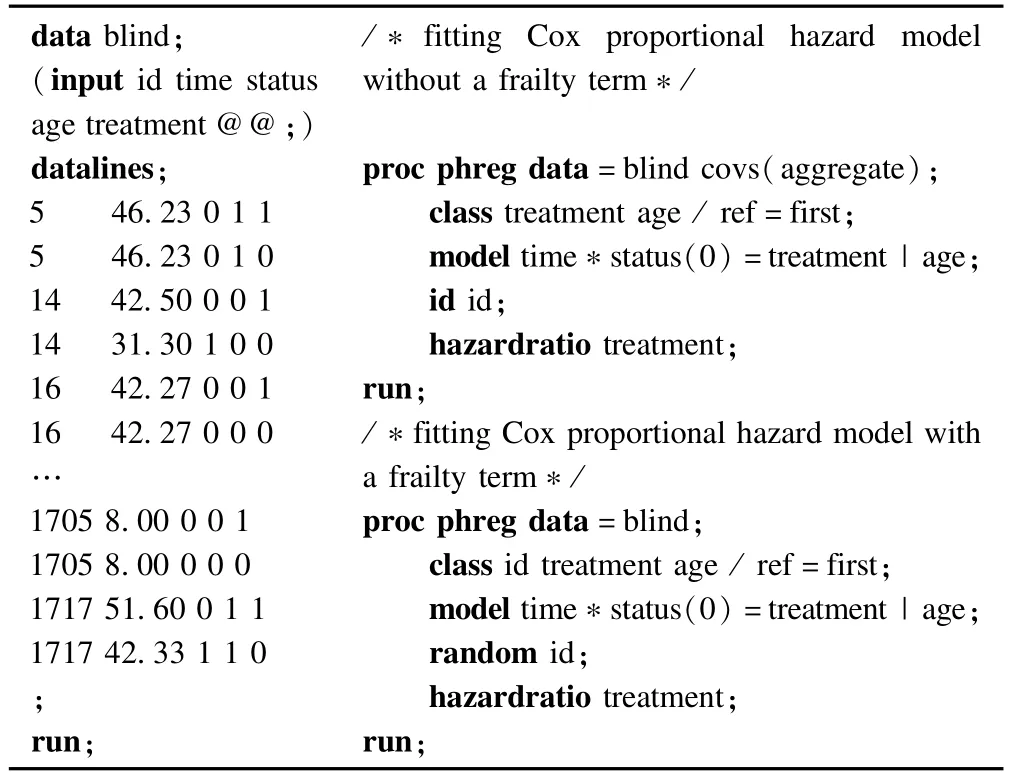
表1 建立數據集和數據分析的程序

2.語句介紹

在SAS 9.3版本的PROC PHREG過程中加入了分析Frailty模型的語句——Random語句。Random語句規定Frailty項服從對數正態分布，即γi～N（0，σ2），其中σ為未知參數，需要估計。Random語句的結構和功能如下：

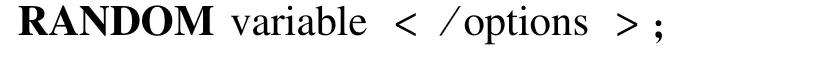
Vaiable是用來指定“群”，它必須是分類變量，即是class語句中的變量。options有如下：

Abspconv＝r，是規定Frailty項對數變換后方差估計時迭代的收斂準則，如果迭代收斂。

Alpha＝value，是規定隨機效應的（1-α）可信區間，默認值是0.05。

Method＝reml｜ml，是規定方差參數估計的方法，默認方法是rem l。

Noclprint，控制在輸出時不打印隨機效應的分類信息表。

Pconv＝r，是規定Frailty項對數變換后方差估計時迭代的收斂準則，如果迭代收斂。

Solution，規定顯示正態分布的隨機效應估計值，同時也顯示對數正態分布的估計值，即Frailty的估計值。

Initialvariance｜initial＝value，規定Frailty項對數變換后方差估計的初始值，默認為1。

3.分析與結果

首先不考慮Frailty項，建立含有變量treatment、age的主效應和交互效應的Cox比例風險模型，然后模型再加入Frailty項，分析程序見表1。為了方便對比，把主要結果列于表2、3。

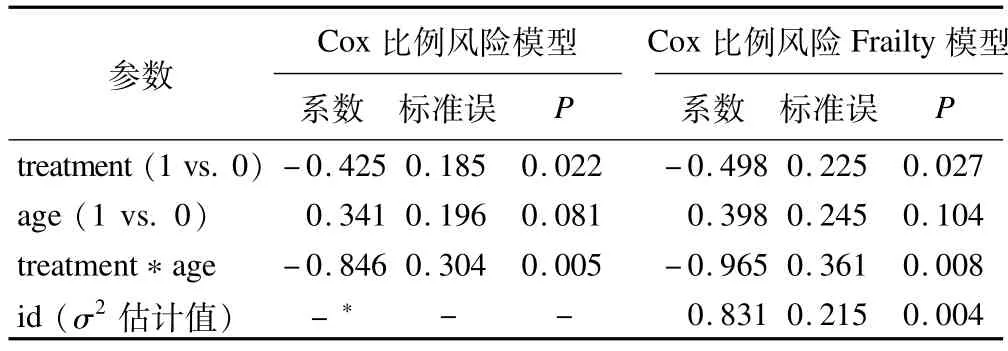
表2 Cox比例風險模型與Frailty模型的參數估計

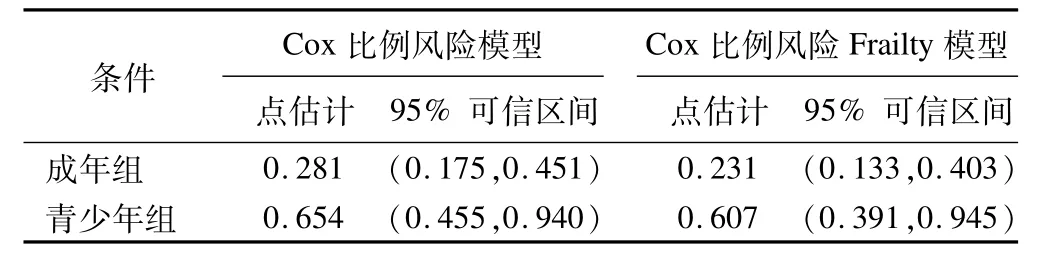
表3 兩個模型的激光光凝治療相對于其他治療的條件風險比估計

從表2可見，Frailty項對數變換后的方差估計值為0.831，與0的差異有統計學意義，提示分析時需要考慮個體間的異質性，有必要在Cox比例風險模型中加入Frailty項。兩個模型的參數估計值相近，Cox比例風險模型比Cox比例風險Frailty模型要保守，在檢驗水準為0.05的情況下，都提示治療方法與發病年齡間存在交互作用。表3給出了不同發病年齡下激光光凝治療相對于其他治療的風險比，從中可看出激光光凝治療方法可延緩眼睛失明進程，并且成年組延緩眼睛失明進程的效果要好于青少年組。

討 論

本質上，Frailty模型是在經典的生存分析的基礎上加入了一個隨機效應，以控制研究對象個體間或組別間存在的異質性。雖然產生異質性的變量也可以通過設置啞變量或用固定效應分析，但固定效應分析方法不是最優的分析方法。按照異質性產生的單位不同，把Frailty模型分為個體Frailty模型、共享Frailty模型兩種。個體Frailty模型假設研究對象個體之間具有異質性，基線風險隨著個體而改變；共享Frailty模型假設組別間具有異質性，基線風險隨著組別而改變，同一組別內的個體享有相同的基線風險。研究對象個體間或組別間存在的異質性是不能忽略，有文章也指出［9-10］：如果有異質性存在，而沒有考慮，會導致效應低估，這點在本文中也有體現——Cox比例風險模型比Cox比例風險Frailty模型要保守，但是兩者的意義是不同的，考慮異質性時效應是條件的效應，不考慮異質性時，效應是邊際效應，在預測時需要注意這點。

與在Cox比例風險模型中引入Frailty項類似，也可以在其它生存分析方法——Weibull回歸模型、加速失效模型中引入Frailty項，擴展生存分析的分析方法。

關于“Frailty模型”的翻譯，有學者譯為“脆弱模型”，但筆者認為有不妥之處。雖然“Frailty”有“脆弱、虛弱等”之意，但是“脆弱模型”所表達出來的意思不能反映“Frailty模型”的本質。結合“Frailty模型”的產生原因與形成思想，筆者反復斟酌，認為譯為“異質性模型”更合適。在沒有規范的譯名情況下，使用“Frailty模型”是最恰當的。

1.Cox DR.Regression models and life tables.JR Stat Soc Series B Stat Methodol，1972，34（2）：187-220.

2.M cGilchrist CA，Aisbett CW.Regression with frailty in survival analysis.Biometrics，1991，47：461-466.

3.Therneau TM，Grambsch PM.Modelling survival data：extending the cox model.Springer：New York，2000.

4.Ha ID，Lee Y，MacKenzie G.Model selection for multi-component frailty models.Stat Med.2007，26（26）：4790-807.

5.Andersen PK，Klein JP，Knudsen KM，et al.Estimation of variance in Cox′s regressionmodel with shared gamma frailties.Biometrics，1997，53（4）：1475-84.

6.Elbers C，Ridder G.True and spurious duration dependence：the identifiability of the proportional hazard model.Review of Econom ic Studies，1982，49（3）：403-40.

7.SAS Institute Inc.SAS/STAT?9.3 User′s Guide.Cary，NC：SAS Institute Inc，2011.

8.Elbers C，Ridder G.True and spurious duration dependence：the identifiability of the proportional hazard model.Review of Economic Studies，1982，49（3）：403-9.

9.Gail MH，W ieand S，Piantadosi S.Biased estimates of treatment effect in random ized experimentsw ith nonlinear regressions and om itted covariates.Biometrika，1984，71（3）：431-44.

10.Yashin AI，Iachine IA，Begun AZ，etal.Hidden frailty：myths and reality.Research report，2001，34，48 pages.

（責任編輯：郭海強）

安徽省自然科學基金（090413126）

1.皖南醫學院預防醫學系（241002）

2.南通出入境檢驗檢疫局

△通信作者：姚應水，E-mail：yingshuiyao＠163.com