三種重復測量資料的統計分析方法比較研究*

秦正積沈 毅△王燕南肖 靜何 書

三種重復測量資料的統計分析方法比較研究*

秦正積1沈 毅1△王燕南2肖 靜1何 書1

目的運用方差分析、多變量方差分析和混合效應線性模型方法探討重復測量資料的統計學分析方法，比較三種方法的統計分析效果。方法用實驗法收集資料，使用excel軟件進行繪圖分析，用SAS軟件進行統計分析。結果GLM多組重復測量方差分析離子種類和鍍金方式及其交互作用有統計學意義、不同時間離子析出差異有統計學意義（所有P＜0.0001）；多變量方差分析離子種類、鍍金方式及其交互作用有統計學意義（所有P＜0.0001）；混合效應模型應用多種方差-協方差結構進行參數估計，以“不規則方差-協方差結構分析”結果最為合理（-2 Res Log Likelihood、AIC、AICC及BIC統計量均最小，分別為894.9，914.9，916.7，930.8），模型顯示離子種類和鍍金方式及其交互作用有統計學意義、不同時間離子析出差異有統計學意義（所有P＜0.0001）。結論三種分析方法各有所長，在運用時應結合資料的特點和實際可行性，擇優選擇分析方法，也可聯合使用，使分析結果更加準確合理。

多組重復測量方差分析 多變量方差分析 混合效應模型

重復測量（repeated measure）是指對同一觀察對象的同一觀察指標在不同時間點進行多次測量。重復測量設計可對觀察指標進行動態觀察或監測，采用較少的樣本含量，能夠控制個體變異，分析更加符合臨床試驗、藥理學及毒理學的特點。重復測量資料的統計分析方法有其廣泛的應用前景［1-5］。

本研究通過分析鍍金對中熔樁核析出離子的影響數據，用三種方法分析離子析出與時間、離子類型的關系，探討重復測量資料的統計分析方法。

對象與方法

本研究以中熔樁核為對象，研究鍍金對中熔樁核析出離子的影響。將18個試件隨機分成3組，每組6個，第1組為對照組，第2組為噴砂鍍金組，第3組為拋光鍍金組。浸泡于人工唾液中，于第1個月，第2個月，第6個月，第8個月分別測其鎳離子、銅離子的濃度，比較3組不同時間離子析出是否不同。

采用excel軟件進行圖表分析，使用SAS統計軟件進行統計分析。

模型簡介

1.多組重復測量資料方差分析

按2個受試者間因素和1個受試者內因素設計的資料的方差分析模型為：

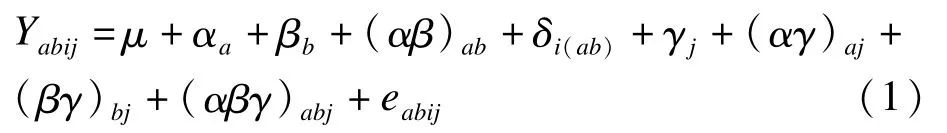
式中Yabij為隨機反應變量，觀察值為yabij。下標a＝1，…，m；b＝1，…，q；i＝1，…，ng；j＝1，…，p。模型中各參數的意義是：μ為總體平均值；αa為因素A在a水平的效應；βb為因素B在第b水平的效應；（αβ）ab為因素A和B在（ab）水平上的交互作用；δi（ab）為第i個受試者在（ab）水平上的效應；γj為重復測量因素C（時間點）在點j的效應；（αγ）aj、（βγ）bj分別為因素A、B與時間點的交互作用；（αβγ）abj屬三因素交互作用；eabij為誤差項［1］。

2.多變量方差分析

具有兩個受試者間因素和一個重復測量因素資料的多變量方差分析模型為：

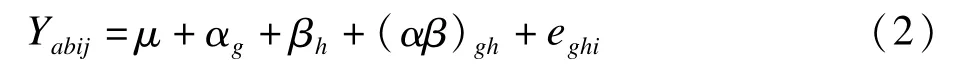
式中：Yabij為隨機變量，它的觀察值為yabij。模型中各參數的意義是：μ為總體平均值；αg為因素A在g水平的效應；βh為因素B在第h水平的效應；（αβ）gh為因素A和B在（gh）水平上的交互作用；eghi為誤差項［1］。

3.混合效應模型

在重復測量模型中，單次測量可視為低水平，個體為高水平，建立混合效應線性模型如下：

Yi是第i受試者的pi×1維反應變量向量。xi為pi×q維已知固定效應設計矩陣。β為q×1維未知的固定效應參數向量。zi為pi×r維已知隨機效應設計矩陣。ri為r×1維未知的隨機效應參數向量。eI是pi×1維隨機誤差向量。［1，6-8］

分析結果

1.概貌分析

（1）各組統計描述

表1 三組試件各月份析出值（±s，μg）

表1 三組試件各月份析出值（±s，μg）

鎳離子銅離子對照 噴鍍 拋鍍第一月6.21±0.73 5.77±1.20 4.44±0.72 9.48±1.78 4.91±1.16 7.38±1.對照 噴鍍 拋鍍47第三月13.82±1.95 12.95±2.75 12.57±2.08 14.00±2.75 7.04±1.61 8.31±1.65第六月144.20±22.96 44.72±8.78 33.52±5.41 373.58±74.78 45.75±10.43 47.20±9.34第八月228.33±34.84 76.67±14.68 56.25±8.95 677.92±134.43 126.67±27.64 138.33±27.49

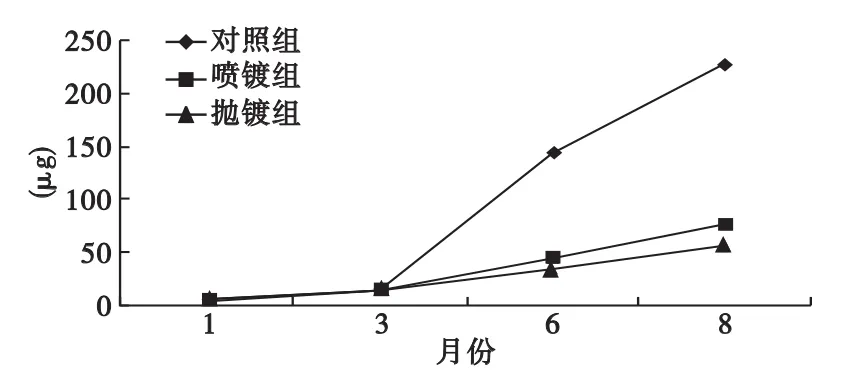
圖1 鎳離子各月份析出趨勢統計圖

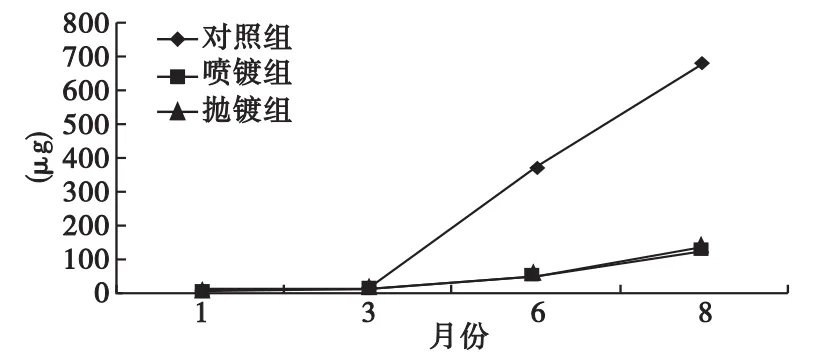
圖2 銅離子各月份析出趨勢統計圖

由表1及圖1、圖2可見，各組鎳離子隨時間增加，析出量在1～3月相差不大，三月到八月離子析出量顯著增加。對照、噴鍍、拋鍍各組鎳離子析出量不同：對照組最多，噴鍍組次之，拋鍍組最少。各組銅離子析出隨時間增加，在1～3月相差不大，三月到八月離子析出量顯著增加。對照、噴度、拋光各組銅離子析出量不同：對照組最多，拋光組與噴度組相差不大，拋鍍組略多于噴鍍組。

2.單變量多組重復測量GLM方差分析

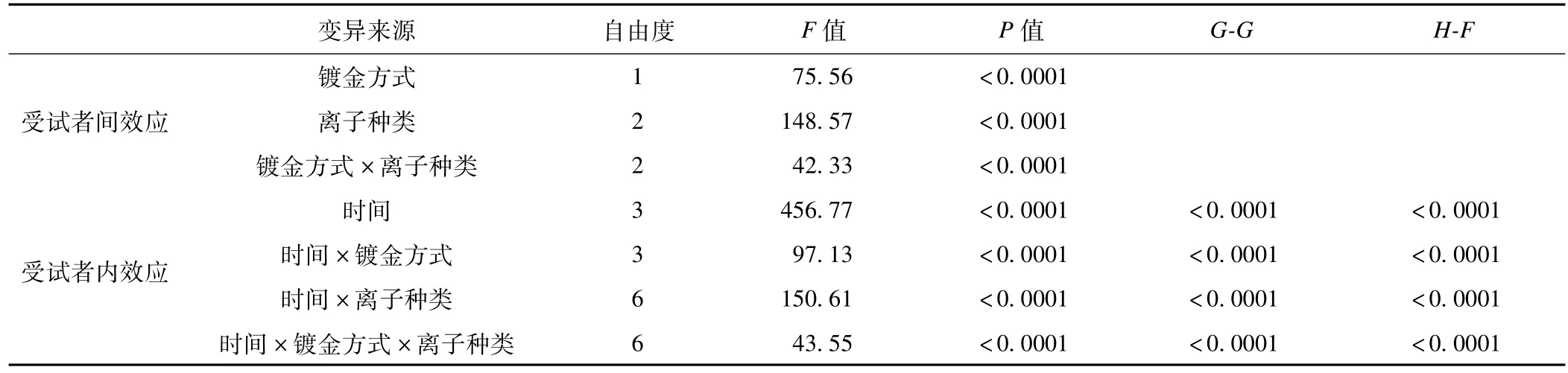
表2 單變量多組重復測量GLM方差分析結果

SAS輸出的Mauchly球性檢驗結果為P＜0.0001，拒絕球性假設，故采用H-F校正概率做出統計學推斷。由表2可知，鍍金方式、離子種類及其交互作用有統計學意義（P＜0.0001）；時間、時間與鍍金方式、時間與離子種類、時間、鍍金方式和離子種類三因素間交互作用有統計學意義（P＜0.0001）。

3.多變量方差分析［1］。

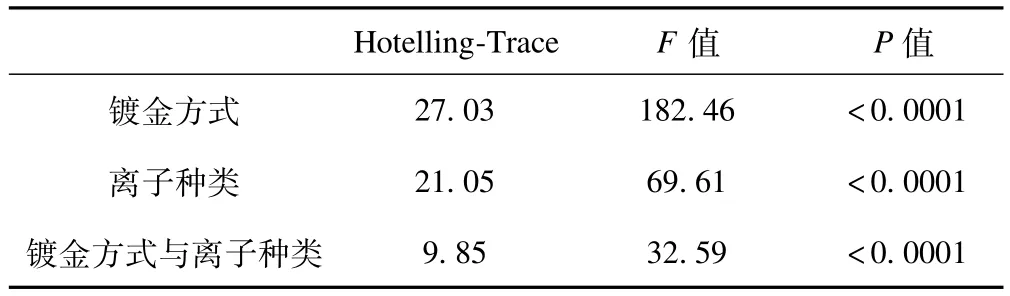
表3 MANOVA全模型分析

用SAS中的GLM過程MANOVA選項完成全模型分析顯示，鍍金方式、離子種類及其交互作用有統計學意義（P＜0.0001）。

4.混合效應模型

在配合混合效應模型時，要選擇合適的協方差結構。

選擇協方差矩陣結構的方法是，在相同模型結構下，選擇幾個不同結構的協方差矩陣，從中選出似然比統計量（-2 Res Log Likelihood）、AIC及BIC較小的一個。如果這些統計量很近似，則選取含參數個數最少的一個。通常以AIC為主要判斷指標［1］。

本模型選用UN，CS，SP（POW），UN（1）和AR（1）五種協方差結構。用SAS計算有關協方差矩陣信息，整理后得到不同協方差的各種檢驗統計量（見表4）。

混合效應模型為：

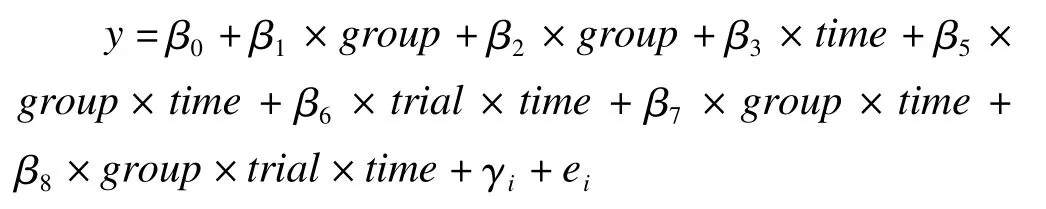
其中，group為離子分組，trial為鍍金方式，time為鍍金時間，γi為隨機效應，ei為隨機誤差，βi（其中i＝1，2，3表示單獨效應的系數，其余為交互效應）為擬合的固定效應系數。

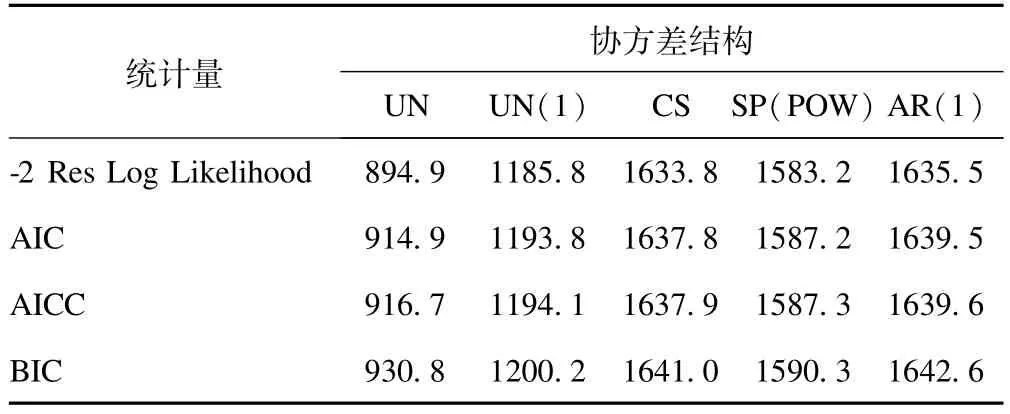
表4 不同協方差結構下的各種檢驗統計量

由表4可知，以UN結構的各種統計量值最小，故選用它作為最適結構。相應的協方差矩陣的第一個區塊結構及協方差參數的WaldZ檢驗結果見表5、表6。

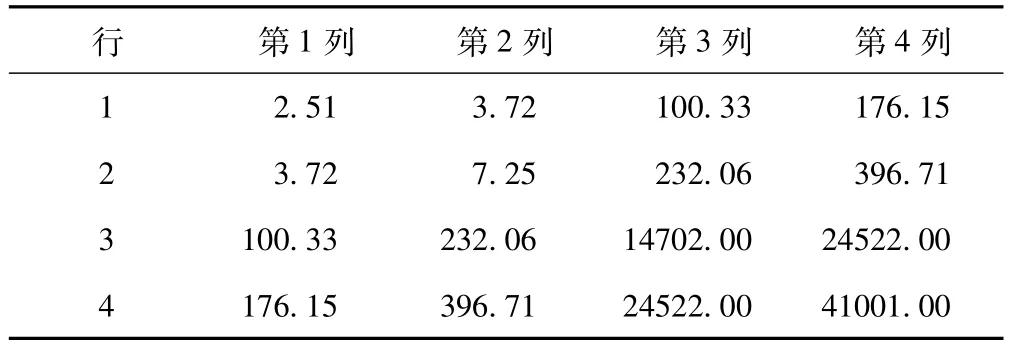
表5 第一個個體的估計R矩陣

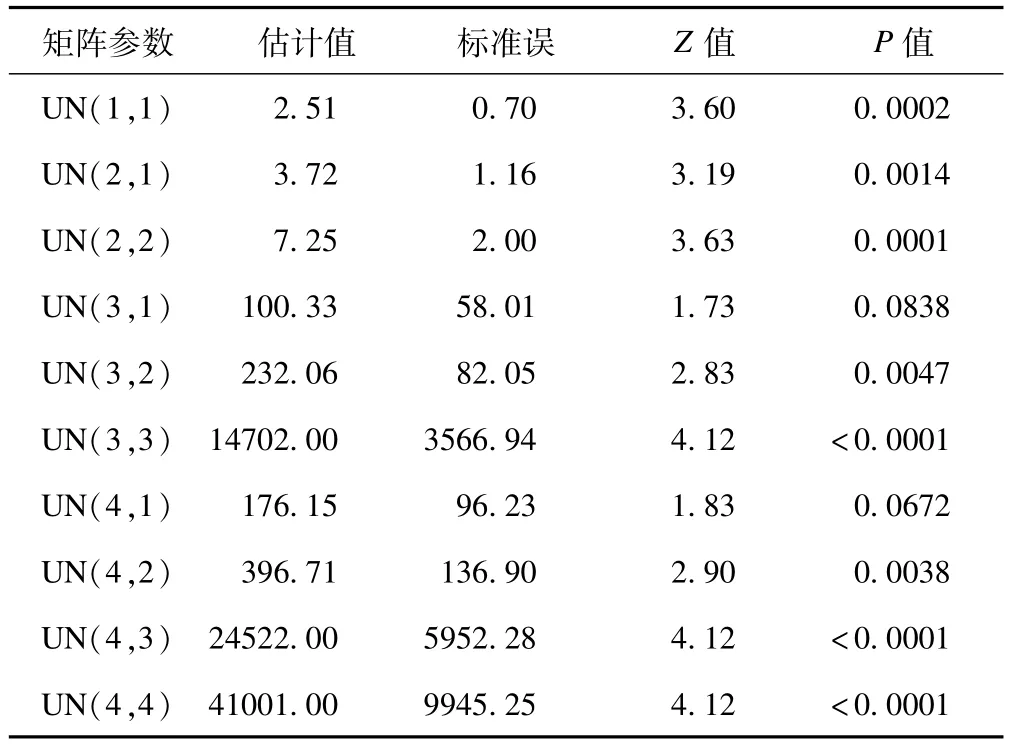
表6 協方差矩陣參數估計值

用UN結構計算的各種固定效應的假設檢驗結果見表7。

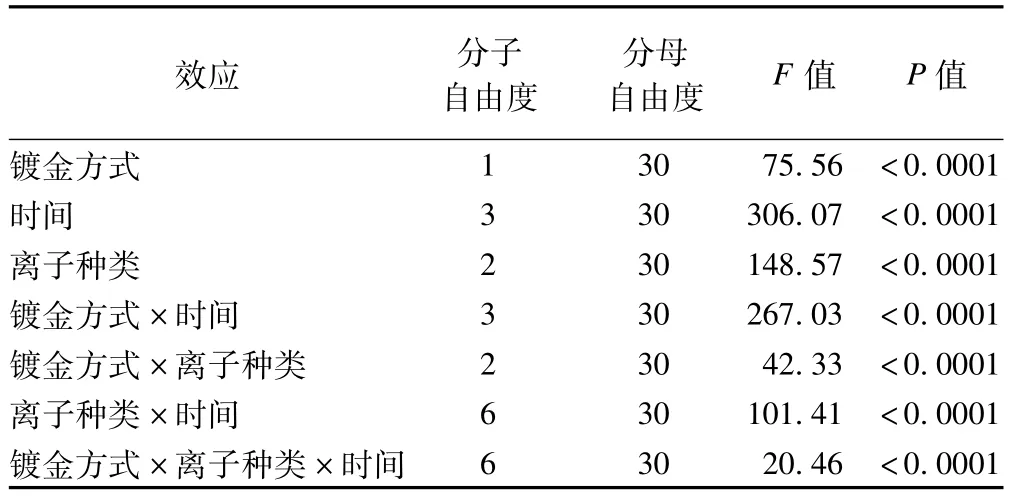
表7 固定效應的檢驗結果

鍍金方式、時間、離子種類、鍍金方式與時間、鍍金方式與離子種類、時間與離子種類、鍍金方式、時間及離子種類、三因素交互作用有統計學意義（均P＜0.0001）。

5.分析結果小結

由上述分析結果可知：采用單變量GLM多組重復測量方差分析，研究得出離子種類、鍍金方式、時間及其三者間的交互作用有統計學意義；多變量方差分析從整體分析出發，未分解時間效應，研究得出鍍金方式、離子種類及其交互作用有統計學意義；混合效應線性模型先進行估計方差-協方差結構參數并評價，然后選用合理的方差-協方差分析得出離子種類、鍍金方式、時間及其三者間的交互作用有統計學意義。

討 論

1.不同模型的分析特點

由前述分析可知：單變量GLM多組重復測量方差分析從固定效應出發，分解出時間效應、受試者間效應和受試者內效應；多變量方差分析從整體分析出發，未分解時間效應；混合效應線性模型先就方差-協方差結構參數進行估計并評價，然后選用合理的方差-協方差分解出固定效應和隨機效應。比較分析結果，可以看出各種分析方法均能得到有關影響因素的效應，但是多變量分析不能得出時間的效應。

2.三種方法的應用探討

（1）單變量多組重復測量方差分析

單變量分析方法對協方差結構有嚴格的要求。在球形結構下只有一個協方差參數，在復合對稱性結構下只有兩個協方差參數，在H型條件下，也只有少數幾個協方差參數。在應用前一定要進行球性檢驗。如不滿足球型條件，建議進行校正。在研究中，GLM模型提供了離子種類、鍍金方式、時間及其三者間的交互作用，結果理論較簡單，容易解釋，而且各大統計軟件如SAS、SPSS、Stata等均能提供單變量重復測量方差分析的結果，信息豐富。因此，在滿足球性檢驗的條件下，應該首選單變量方差分析［1］。

（2）多變量方差分析

多變量方差分析是單變量方差分析的擴展，對協方差結構沒有要求，要估計盡可能多的方差及協方差參數。同時對多個反應變量進行方差分析，累積多個反應變量的信息從而得出統一的統計學結論。它著重分析受試者在多個反應變量基礎上的整體信息，而不是個別反應變量的單獨信息。當我們把重復測量資料在p個時間點上的反應變量測量值看作p個反應變量時，就是一種多變量資料，因此可以用多變量方差分析模型來分析重復測量資料而不存在任何理論問題。

多變量方差分忻因為對協方差矩陣完全無限制，理論上應用范圍更廣。但這一特點也使臨床試驗千差萬別的試驗數據的復雜關系失去意義，只能得到各時間點數據的整體結論。在研究中，僅提供了鍍金方式、離子種類及其交互作用的效應，沒有提供時間的效應［1］。

（3）混合效應線性模型

基于似然函數法原理的混合效應線性模型分析方法，是一般線性模型的擴展。它允許資料存在某種相關性及協方差矩陣的多樣性，從而能更好地適應重復測量資料的特點［8］。其次，一般線性模型只能分析固定觀察時間點數目相等的資料，不能分析觀察時間點不等的資料。此外，在一般線性模型中，對具有缺失觀察值的受試者是完全舍棄不用的，丟失了資料信息。而混合效應線性模型也能充分利用具有缺失觀察值的受試者資料［5］。

混合線性模型在其應用上具有如下特點：

（1）對固定效應參數進行更準確的估計：混合線性模型考慮到了數據的聚集性問題，并用了相應的迭代方法，可以獲得回歸系數的有效估計，提供正確的標準誤，從而假設檢驗的結果更加準確。它比傳統方法更“保守”，后者的標準誤是通過簡單的忽略聚集的存在而獲得，往往并不準確。

（2）重復測量資料的分析及規律探討：傳統模型也可以對重復測量資料分析，要求數據是平衡的。但在實踐上，測量次數常是不規則的，此時傳統模型的估計可能有誤。而混合線性模型可以處理任何測量模式的數據，并提供無偏的參數估計。因此其分析的準確性得到提高［7］。

混合線性模型可以處理不同形式的協方差矩陣，對時間因素的效應且內部關系又極為復雜的研究極為有用［8］。由于引入了隨機效應，結果更具有外推性［4，6］。本研究中，既能得到固定效應，又能分析出隨機效應，同時能得到時間效應的變化規律，使研究結果更可靠。

綜上所述，三種分析方法各有所長，在運用時應結合資料的特點和實際可行性，擇優選擇分析方法，也可聯合應用使分析更豐富、更準確、更合理。

附 件：有關SAS程序

1.余松林，向惠云.重復測量資料分析方法與SAS程序.北京：科學出版社，2003，1-2.

2.陳峰，任仕泉，陸守曾，等.非獨立計量資料的內部相關性研究.現代預防醫學，1998，25（3）：269-271.

3.任仕泉，陳峰，楊樹勤，等.非獨立數據及其協方差結構表達.中國衛生統計，1998，（4）：4-8.

4.陳峰，任仕泉，陸守曾，等.非獨立試驗的組內相關與廣義估計方程.南通醫學報，1999，19（4）359-362.

5.黃坤.混合線性模型在臨床試驗中重復測量資料的應用.現代預防醫學，2005，32（11）：1584-1585.

6.張文彤.SPSS11統計分析教程.北京：北京希望電子出版社，2002，65-76.

7.王超.混合效應線性模型與單因素方差分析在重復測量數據中的應用比較.數理醫藥學雜志，2006，19（4）：355-357.

8.Cnaan A Laird N M，Slasor P.Using the general linear m ixed model to analyze unbalanced repeatedmeasures and longitudinal data.Statistics in Medicine，1997，16：2349-2380.

（責任編輯：郭海強）

*：南通大學校自然（03041051）；教改課題（2013B116）

1.江蘇南通大學公共衛生學院流行病與醫學統計學教研室（226019）

2.浙江寧波市鄞州區章水社區衛生服務中心

△通信作者：沈毅，E-mail：stata70＠sohu.com