互聯電力系統可靠性評估

何向剛，蔣澤甫，唐學用

(貴州電網公司電網規劃研究中心，貴陽 550002)

互聯電力系統可靠性評估

何向剛，蔣澤甫，唐學用

(貴州電網公司電網規劃研究中心，貴陽 550002)

基于隨機網流模型的多域互聯電力系統可靠性評估方法，以系統元件限制的最大網流模擬實際電力系統的潮流，能有效進行多域互聯電力系統可靠性的評估，提高計算速度。然而，多域互聯電力系統結構復雜、元件繁多，狀態枚舉困難，面臨維數災問題。本文以隨機網流模型為基礎，提出邊際容量、遞增搜索等概念，用于多域互聯電力系統可靠性評估中。算例分析表明，改進方法極大地減少了枚舉狀態數，提高了可靠性評估效率；并驗證了所提出的方法的有效性和正確性。

可靠性；邊際容量；遞增搜索法；隨機網流法

0 前言

為了實現資源互補和提高電力系統的運行安全性，將中小型電網通過聯絡線互聯形成多域互聯電力系統是非常必要的。目前我國各大區及省間已逐步實現了聯網，聯網形式也從簡單的雙邊聯網轉為復雜的互聯形式。電力系統互聯后，各系統可以通過聯絡線從其它系統得到電力，實現互聯各子系統之間的相互支援，獲得了水火電互濟，錯峰和互為備用等效益。從而提高整個大區的可靠性水平。

國內外許多學者對電力系統可靠性計算進行了大量研究工作[1-6]，但對互聯電力系統可靠性計算研究文獻較少。Billinton[7-11]等人提出的支援容量法，即在考慮各種約束條件下，將外部系統等效為一個多狀態的發電機-負荷組，然后重點研究包含發電機-負荷組的自身系統的可靠性水平。文獻 [12]考慮了互聯系統負荷的錯峰及同時率、聯絡線容量及其可用率、各系統的容量及電量約束等問題，提出了評估兩系統互聯的可靠性效益的算法。

文獻 [13]提出了一種改進的分塊法，可以解決環型聯結的互聯系統的可靠性評估問題，但計算工作量較大。文獻 [14]提出了基于元件強迫停運率的區域發電可靠性指標靈敏度表達式，能夠根據靈敏度的大小判斷對系統可靠性影響較大的關鍵環節和薄弱環節。文獻 [15]采用以路徑為基礎的隨機網流法，研究任意網絡結構的多域互聯電力系統的可靠性，把握住網絡拓撲和支路輸電容量這兩個關鍵的因素，解決了電力系統中交流與直流潮流計算時不考慮支路的允許載流量而造成計算結果不一定可行的問題，計算快捷，取得較好的效果。但是，文獻 [15]只考慮了某一參考點t在互聯以后的可靠性，沒有給出整個電網的可靠性指標，直接利用其進行系統可靠性評估時，依然面臨狀態數多、可能造成維數災的問題。

文中以隨機網流法為基礎，提出邊際容量概念，利用遞增搜索法以減少多域互聯電力系統可靠性評估的狀態數、提高系統可靠性評估效率。充分考慮各系統內部電力及能量約束、機組計劃檢修、聯絡線的容量約束及隨機故障等影響，進行多域互聯電力系統高可靠性評估。

1 隨機網流法的數學模型及算法

1.1 網的定義

網是由有容量限制的支路構成的圖[6]。參與互聯的各個電網稱為子系統，忽略系統內部電網結構的影響，認為系統內的發電機并聯連接于一個節點，且與聯絡線直接相連。聯絡線支路代表子系統間的連接，包括一條或多條聯絡線。各子系統的等效負荷等于各個子系統的內部負荷總和。

圖1所示，圖中有N個子系統，N個等效負荷；設互聯系統中有Nb條聯絡支路，有相應的容量CK，對應聯絡線某狀態的容量；子系統與虛構的發點S通過虛擬支路S1，S2…SN相連，各虛擬支路容量與相應子系統某狀態的容量相等；系統中負荷都用與虛構的收點T通過虛擬支路D1，D2…DN相連，各虛擬支路容量與相應的負荷大小相等。圖1中的總支路數NT為：

整個互聯系統總負荷為DL

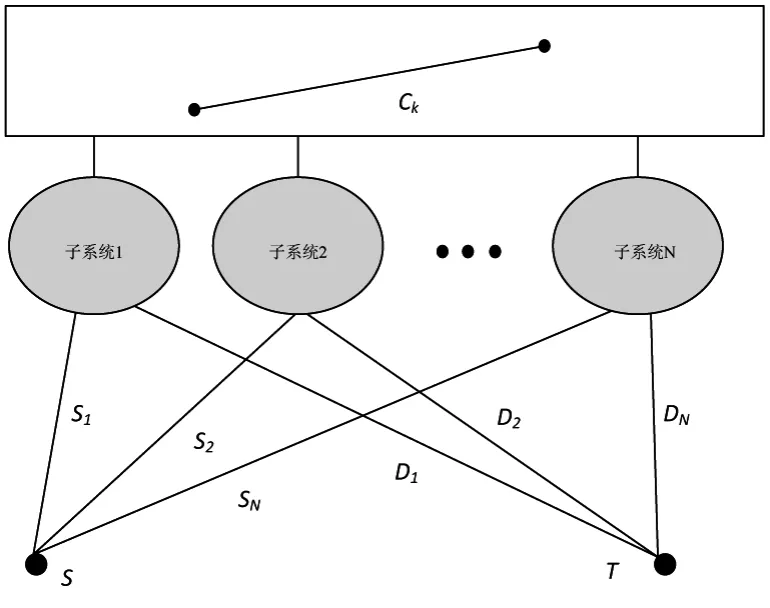
圖1 互聯電力系統網絡模型

1.2 隨機網流法

隨機網流法[16]即用系統中各元件容量限制下的網絡最大流來代替實際電力潮流。在可靠性評估中，網絡最大流表示網絡的最大傳輸能力。網絡最大流的計算如下：

設從S到T的最小路集為L={L1，L2··· Lm}，其中m為最小路數；列舉互聯子系統的一種狀態和互聯支路的一種運行狀態，根據列舉的運行狀態，比較各最小路元件的傳輸容量，得到各最小路的最大流 {f1，f2，···fi···fm}。則該狀態下網絡最大流為DT，即

2 互聯系統可靠性評估及其改進

失負荷概率 (LOLP)和失負荷功率(EDNS)為電力系統可靠性評估的兩個重要指標，下面介紹互聯電力系統可靠性評估中上述兩個指標的計算模型。

2.1 子系統和聯絡線裕度表

設已知元件的各種運行狀態的確切概率P(Xi)(i=0，1，2···n)；n為元件的狀態數。

設Va和Vb分別為元件a、b的容量，裕度表按一定步長ΔX給出，則有

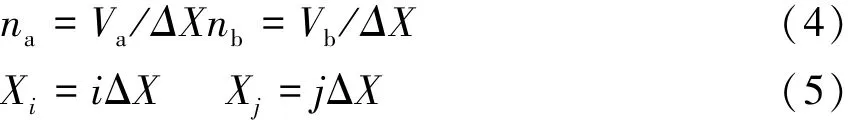
na和nb分別為元件a、b的狀態數；Xi和Xj分別表示元件a、b的狀態，為了簡便起見，下面的敘述中將用i代表Xi，用j代表Xj。

當兩個元件并聯組合時，組合元件的裕度容量等于兩個元件裕度容量之和。因此組合元件c在Xk的確切概率可以表示為[17-18]：

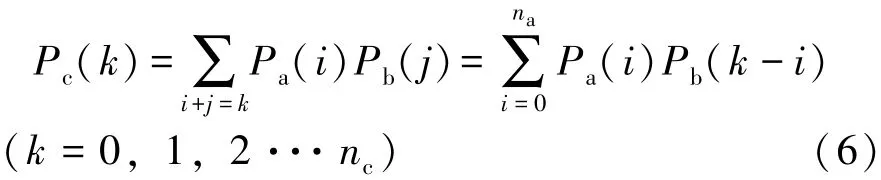
組合元件c的狀態數為nc=na+nb。

按照上述方法可以形成并聯元件的裕度表，由于各子系統中發電機之間、子系統間聯絡線之間都屬于并聯關系，所以可以按上述方法分別形成各子系統和聯絡線裕度表。

2.2 系統可靠性指標的計算

失負荷的概率 (LOLP)、系統失負荷功率(EDNS)可由下面的式子求得

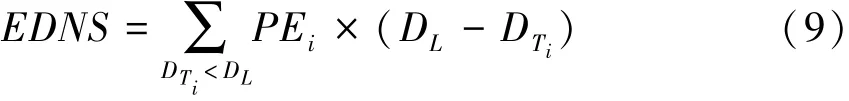
式中：NM為聯絡支路與子系統裕度表總數；PEi為第i種運行狀態的概率；DTi為第i種運行狀態下可滿足的負荷。

在此基礎上，互聯發輸電系統的可靠性指標可按圖2所示流程圖求出。

2.3 互聯系統可靠性計算的改進

隨著互聯子系統數目的增加，互聯線路回數的增多以及互聯結構日趨復雜，用上述計算方法枚舉所有的運行狀態，計算量很大，甚至達到無法計算的程度。為了減少枚舉的狀態數，本文提出了邊際容量的概念和遞增搜索算法。

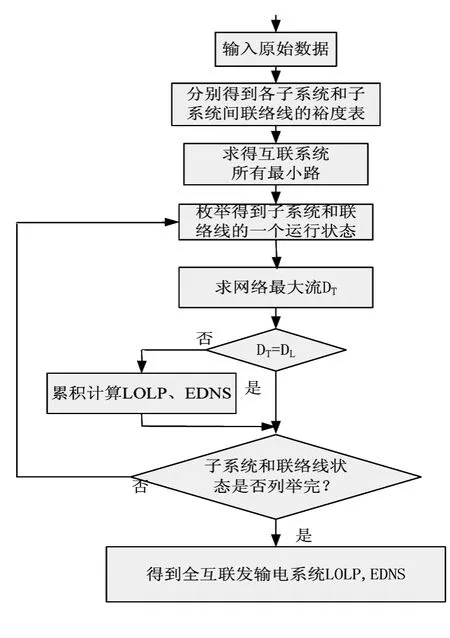
圖2 求解可靠性指標流程

2.3.1 邊際容量

由于機組強迫停運率很小，在并聯卷積得到的子系統裕度表中，確切概率隨故障階數的相對變化比裕度容量隨故障階數的相對變化要快，所以決定失負荷大小的主要因素是確切概率。減少計算量的情況下盡量不影響計算精度，可以忽略發電機高階故障，從而引入了邊際容量 (MC，Marginal Capacity)的概念，邊際容量根據故障階數來確定，繼而確定計算范圍。如果考慮某子系統的最高階故障為HS階，則取MC為該子系統中容量最大的HS臺機組容量之和，設該子系統總容量為TC，則只需計算裕度大于等于TC-MC的裕度狀態。同理，可以確定聯絡支路邊際容量。

又由于裕度表中隨故障階數的增加確切概率變小，逐漸提高故障階數，可靠性指標變化會越來越小。考慮到各子系統和各聯絡支路分別高一階故障的情況，如果兩次計算的結果相差不大，說明選取的故障階數合理。相差大小的判據視需要的計算精度而定。

2.3.2 遞增搜索法

為了減少枚舉的狀態數，本文提出了遞增搜索算法。下面以一個多元不等式方程求解為例，來說明遞增搜索算法的原理。

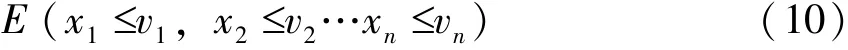
式中：x1，x2…xn為函數變量；F表示x1，x2…xn之間的函數關系，且F對每個變量均單調遞增；E為一定值；v1，v2…vn均為定值。求該多元不等式方程的自然數解集。將n個變量編號，用一個n位數來表示一組變量的解，這個n位數各位上的數字代表變量的值。設n個變量中取值范圍最大的為vi，則取[vi]為該n位數的進制。將這個n位數從小到大遞增，可以得到該不等式方程的所有自然數解集。

在遞增的過程中，由于函數F對每個變量均單調遞增，當枚舉到一組自然數不滿足不等式方程時，n位數各位均高于該組自然數的自然數集都不滿足不等式方程，可以跳過這些自然數集的枚舉，減少枚舉數組，從最低位開始尋找非零位，如該非零位上一位不為最大值，則上一位進1，該位及比該位低的數位上的數字歸零，如上一位對應的自然數為最大值，則繼續向上尋找對應的自然數不為最大值的位，找到后在該位加1，比該位低的數位上的數字歸零，直到大于n位數的最大值，求得該多元不等式方程的自然數解集。

表1 需要計算的數組

利用上述遞增搜索法實現的步驟如下。假設有Nl條聯絡支路，NS個子系統，總的裕度表個數NM為Ns+Nl，則各個裕度表狀態的組合便是整個互聯系統的狀態。將NM個裕度表編號，用一個NM位數各位上的數字代表對應編號的裕度表的狀態。設NM個裕度表中狀態數最多的狀態數為nmax，則取nmax-1為該NM位數的進制。將這個NM位數從小到大遞增，可以枚舉所有需要評估的網絡狀態。枚舉到一種運行狀態滿足負荷要求時，比它大的裕度狀態亦都可以滿足負荷要求，跳過這些裕度狀態的枚舉，直到大于該NM位數的最大值。

3 算例

為了說明文中提出的方法使得多域互聯電力系統的可靠性計算達到了實用的程度，表3分別列舉了包含4、5個子系統的互聯電力系統的分析。其中系統元件和可靠性參數如表2所示，通過該算例可以看出，本文提出的方法與完全枚舉所得的可靠性指標誤差均在1.4%以內，評估次數減少了百萬次以上，從而大大減少了評估所需要的時間，提高了計算的效率。

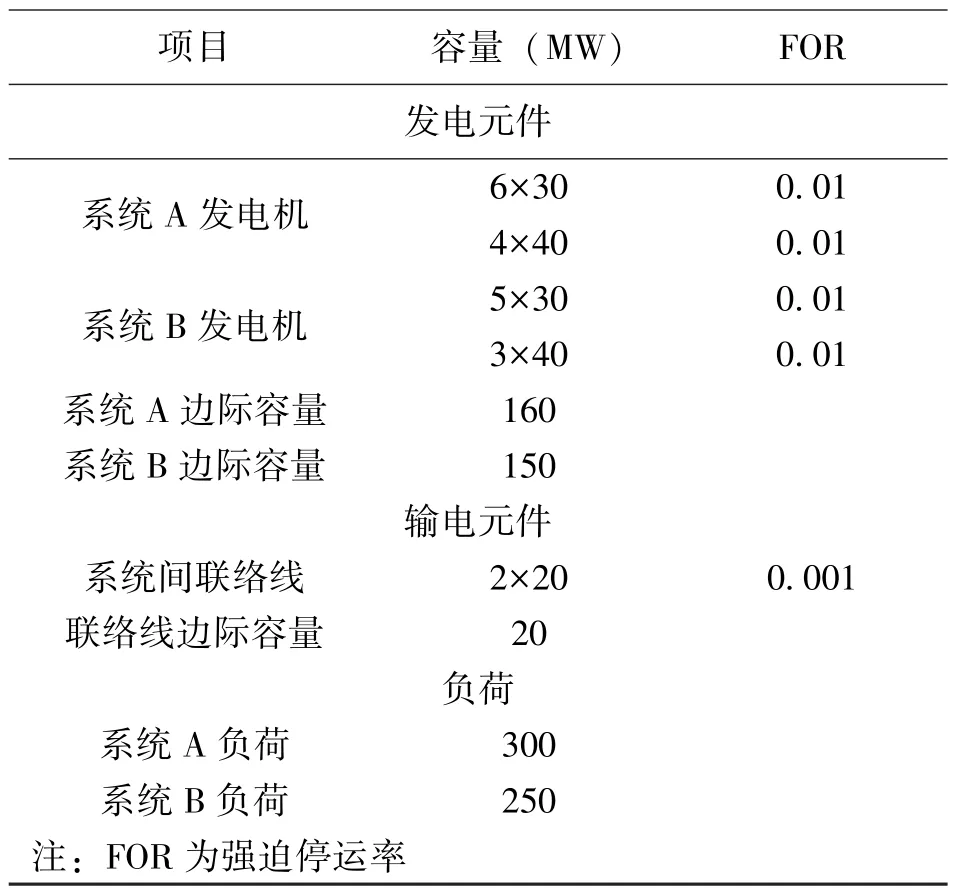
表2 發電元件和輸電元件參數

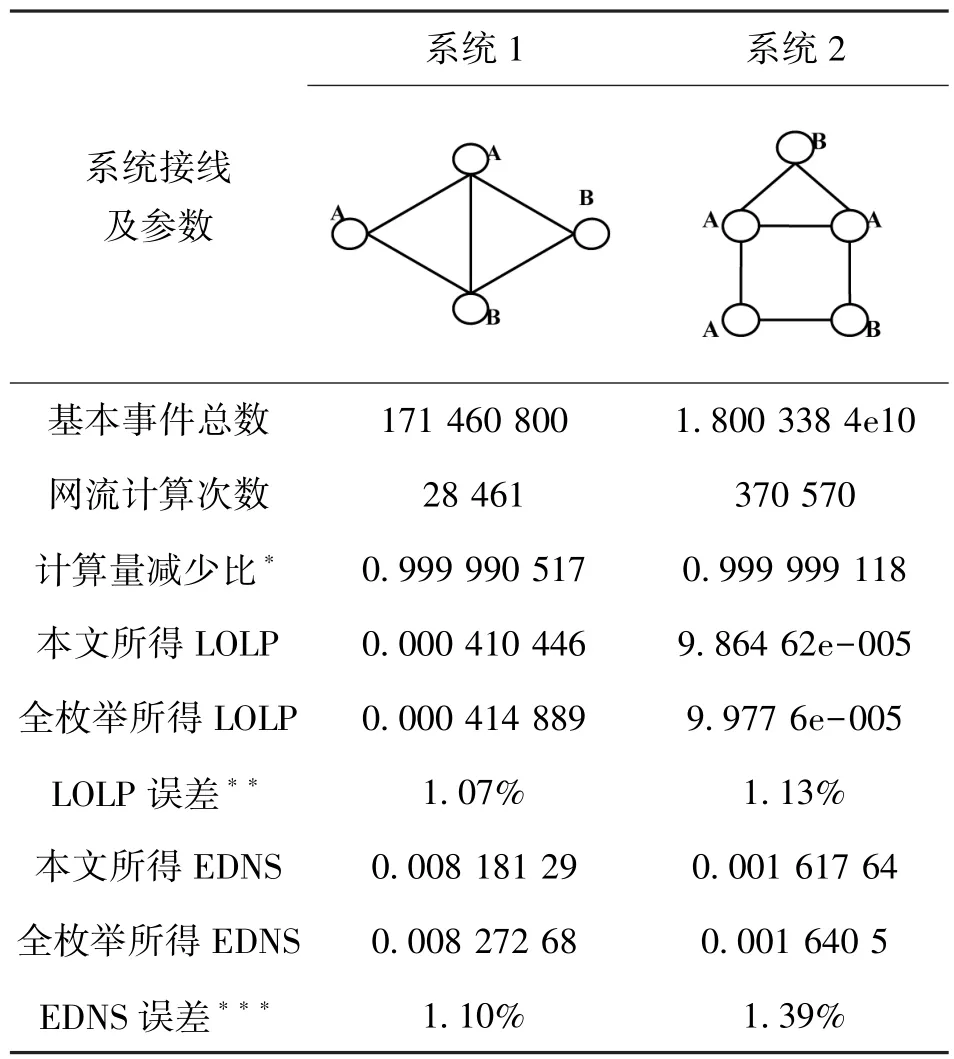
表3 兩個數字算例的計算結果

4 結束語

文中采用隨機網流模型進行多域互聯電力系統可靠性的評估，解決了以往的互聯可靠性分析計算方法只能解決鏈型或輻射型連接的問題，有效地處理了環網可靠性分析困難的問題，可得到全網的可靠性指標。同時，為了提高可靠性評估的效率，本文引入邊際容量以在合理的精度范圍內忽略發電機和聯絡線高階故障；提出并利用遞增搜索法，極大地減少了枚舉次數。理論分析和實際算例證明了該模型有效性及正確性。

文中只采用該模型對整個系統的可靠性進行了分析，對于多域互聯電力系統來說，分析各子系統在互聯以后可靠性得到的提高，互聯所帶來的效益，也具有實際的意義。今后對此問題應進一步研究。

[1] 郭永基.電力系統及電力設備的可靠性 [J].電力系統自動化，2001，25(17)：53-56.

[2] 王景辰，李孝全，楊洋，等.基于交叉熵的蒙特卡洛法在發電系統充裕度評估中的應用 [J].電力系統保護與控制，2013，41(20)：75-79.

[3] 王勇，韓學山，丁穎.計及站內接線的電網可靠性評估的蒙特卡羅方法 [J].電力系統保護與控制，2012，40 (5)：53-58.

[4] 劉文霞，蔣程，張建華，等.一種用于序貫蒙特卡羅仿真的風電機組多狀態可靠性模型 [J].電力系統保護與控制，2013，41(8)：73-80.

[5] R N Allan，R Billinton，A M Breipohl，et al.Bibliography of the application of probability methods in power system reliability evaluation 1987-1991[J].IEEE Transactions on Power Systems，1994，9(1)：41-49.

[6] R N Allan，R Billinton，A M Breipohl，et al.Bibliography of the application of probability methods in power system reliability evaluation 1992-1996[J].IEEE Transactions on Power Systems，1999，14(1)：51-57.

[7] Roy Billinton，Mahmud Fotuhi-Firuzabad，Lina Bertling.Bibliography of the application of probability methods in power system reliability evaluation 1996-1999[J].IEEE Transactions on Power Systems，2001，16(4)：595-602.

[8] Nurul A，Chowdhury，R Billinton.Assessment of spinning reserve in interconnected generation systems with export/import constraints[J].IEEE Trans.on Power Systems，1989，4 (3)：1102-1109.

[9] M E Khan，R Billinton.Composite system spinning reserve assessment in interconnected systems[J].IEE Proc.Gener. Transm.Distrib，1995，142(3)：305-309.

[10] Roy Billinton，Wei Zhang.An adequacy equivalent approach for composite power system reliability evaluation[J].IEE Proceedings on Power and Computing，1995：163-168.

[11] Roy Billinton，Wei Zhang.Enhanced adequacy equivalent for composite power system reliability evaluation[J].IEE Proceedings on Generation，Transmission and Distribution，1996，143(5)：420-426.

[12] 王秀麗，曹成軍，王錫凡.互聯系統可靠性效益評估方法[J].電網技術，2000，24(7)：1-5.

[13] Li Y，Singh C.A directed method for multi-area production simulation.IEEE Trans on Power Systems，1999，14(3).

[14] 萬軍平.基于元件強迫停運率的互聯系統可靠性指標靈敏度分析 [J].電力系統保護與控制，2009，37(21)：15-20.

[15] 王錫凡，孫啟宏.研究多域互聯電力系統可靠性的網流法 [J].西安交通大學學報，1984(4)：41-52.

[16] 王錫凡.電網可靠性評估的隨機網流模型 [J].電力系統自動化，2006，30(12)：1-6.

[17] 王錫凡.電力系統優化規劃 [M].北京：水利電力出版社，1991.

[18] 郭永基.電力系統可靠性原理和應用 [M].北京：清華大學出版社，1986.

Research on Improved Reliability Evaluation For Multi-area Interconnected Power System Based on Probabilistic Network-flow Model

HE Xianggang，JIANG Zefu
(Power Grid Planning and Research Center，Guizhou Power Grid Corporation，Guiyang，550002，China)

Probabilistic network-flow model is presented in evaluating reliability of multi-area interconnected power system.Compared with actual power flow，the presented model can solve the reliability evaluation of multi-area interconnected power system more effectively.To avoid the curse of dimensionality caused by the state-enumeration of multi-area interconnected power system with many elements，the conceptes of marginal capacity and incremental search are proposed to assess the reliability of multi-area interconnected power system based on the probabilistic network-flow model to reduce the enumerated state number.Practical results confirm the proposed method is valid in assessing overall reliability of multi-area interconnected power system.

reliability；marginal capacity；increased search method；probabilistic network-flow

TM744

B

1006-7345(2014)06-0026-05

2014-12-16

何向剛 (1982)，男，碩士，工程師，貴州電網公司電網規劃研究中心，從事電力系統規劃、電力系統可靠性分析研究工作(e-mail)525153231＠qq.com。

蔣澤甫 (1977)，男，博士，工程師，貴州電網公司電網規劃研究中心，從事電力系統規劃與可靠性、風電集成及系統可靠性等方面的研究工作 (e-mail)jiangzefu＠126.com。