一種基于CMAC神經網絡的板形模式識別新方法

李 艷，張自立，呂建紅

(1.軍械工程學院信息工程系，河北石家莊 050003;2.石家莊學院計算機學院，河北石家莊 050035)

板形模式識別是冷軋帶鋼生產的核心。其主要 任務就是將檢測到的板形應力分布離散值，經過一定的數學方法進行適當的模式分解，得到板形特征參數值，為控制系統提供控制策略。

隨著板形識別和控制精度要求的提高，提出了板形模式識別的模糊分類方法和神經網絡板形模式識別方法，其中應用最廣的方法是神經網絡方法。目前，神經網絡用于板形識別的嘗試是將帶鋼沿寬度方向所有測量區的板形缺陷值作為輸入送入神經網絡，輸出為對應板形缺陷基本模式的隸屬度。這種方法需要的輸入量多，網絡結構復雜，加大了網絡學習的工作量，而且對于不同寬度的帶鋼需要不同的網絡拓撲結構，因而通用性和實用性不強［1］。

為此建立了一種新的CMAC(小腦模型聯接控制器)網絡識別模型。該網絡模型在訓練中引入了動態學習率來調整權值。這種模型有效地解決了傳統板形識別模型的不足。仿真結果表明，這種模型大大提高了板形識別的精度和速度。

1 基于CMAC的板形模式識別模型

1.1 板形識別的基模式

軋后板形表現為縱向殘余應力δ(y)的橫向分布。此殘余應力滿足其自相平衡的條件，即沿板寬的積分值為零，如式(1)所示。

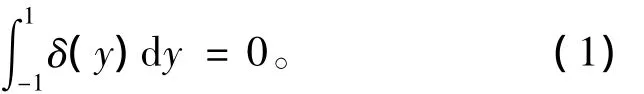
式(1)中y為橫向相對坐標，從板的一邊到另一邊，y從－1變化到+1。式(1)稱為板形的基本性質。

由于控制方法的限制，工程上常見的板形識別信號基本模式包括左邊浪、右邊浪、中間浪、雙邊浪、右三分浪、左三分浪、四邊浪、邊中浪等。每一種模式所對應的殘余應力仍然需要滿足式(1)。對上述8種模式的殘余應力分布進行歸一化處理，將其定義為板形的基模式。選用一次、二次、三次、四次勒讓德正交多項式表示上述4對兩兩互反的8種板形基模式所對應的殘余應力分布［2］，如圖1所示。

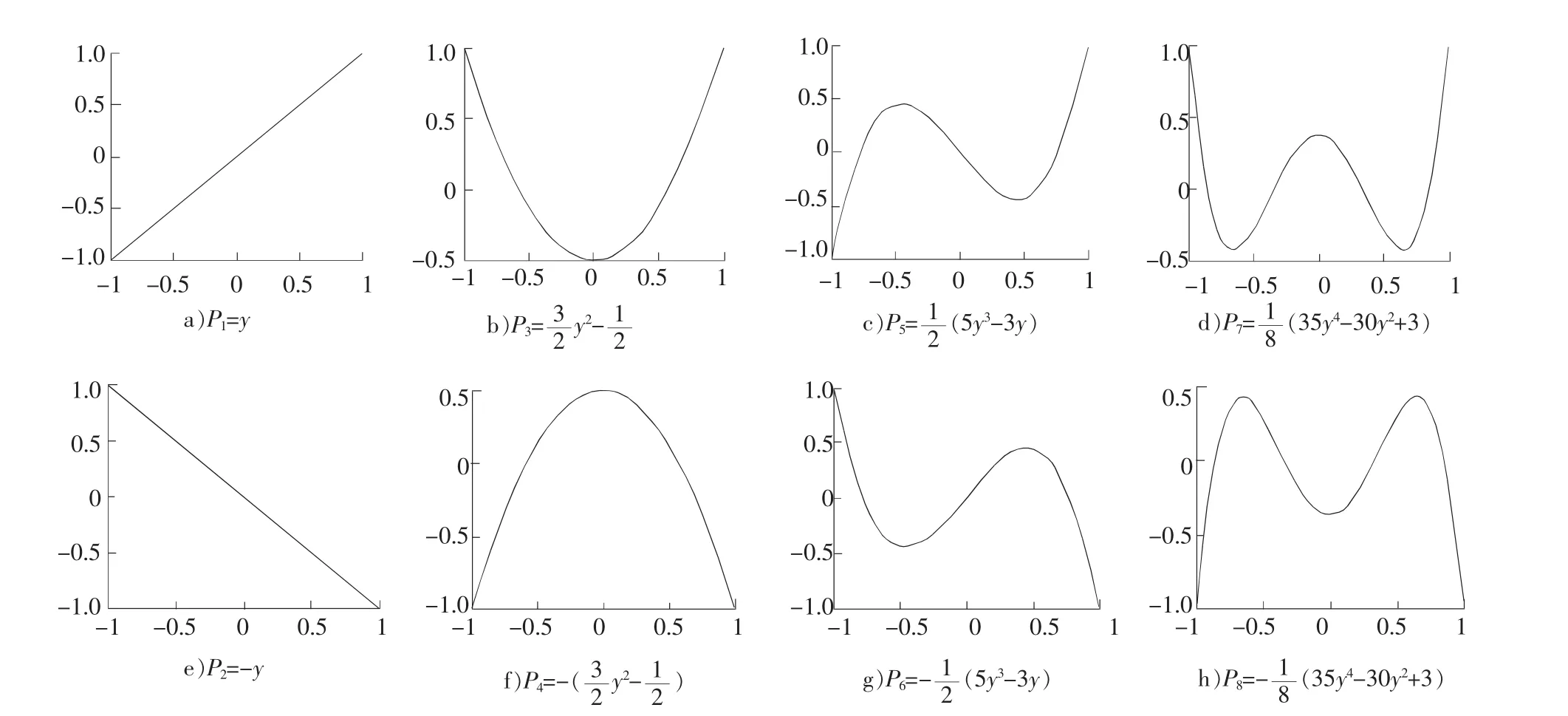
圖1 板形基模式應力圖Fig.1 Basic patterns of flatness

圖1所示的板形基模式曲線，均滿足式(1)表示的板形基本性質。所以選用勒讓德正交多項式表示板形是較合理的。一般地，軋后板形可表示為基模式板形的線性組合，如式(2)所示。

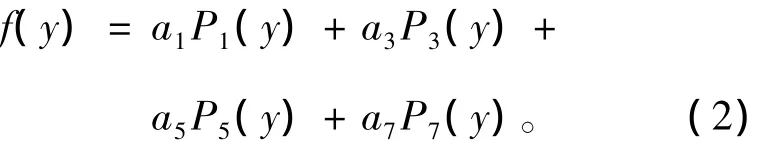
其中P1，P3，P5，P7分別表示一次、二次、三次、四次勒讓德正交多項式。a1，a3，a5，a7分別表示板形的線性特征系數、二次特征系數、三次特征系數和四次特征系數。

可見，板形識別實際上是經過數學運算，提取出板形的基模式系數或特征系數 a1，a3，a5，a7。由于a1，a3，a5，a7均可為正或負，故可分別表示上述8種板形基模式分量的大小。

1.2 基于CMAC網絡的板形模式識別模型輸入神經元的確定

傳統的板形識別模型在識別板形時，直接將n個實測板形應力信號作為網絡的輸入，所以網絡的拓撲結構是由軋件的寬度決定的。然而，對于寬帶冷軋機，需要有多個不同拓撲結構的神經網絡才能完成板寬變化時的識別任務。為了解決這個問題，近年來的識別模型中采用了基于歐式距離［2］的神經網絡板形模式識別方法。它將待識別樣本與基本模式的歐式距離作為網絡的輸入，則網絡輸入節點的數目由基本模式的數目決定。由于現階段冷軋帶鋼的基本模式數目通常由實際生產決定，因此輸入節點的數目是確定的，網絡結構固定，較之多點板形應力信號值作為模型輸入的思想，大大減少了輸入節點的個數，簡化了網絡結構，在精度及控制的復雜程度上都取得了非常大的進展。

待識別樣本y與第k個標準樣本的歐式距離如式(3)所示。

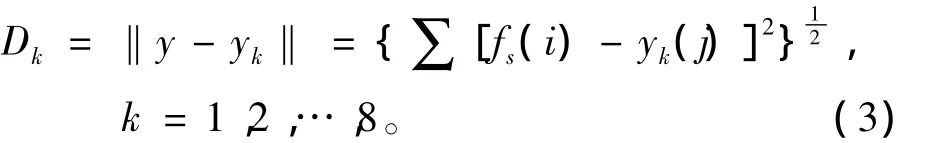
式中:y=(fs(1)，fs(2)，…，fs(n))表示實測的待識別樣本歸一化函數;yk=(yk(1)，yk(2)，…，yk(n))為8個標準樣本歸一化函數。

將Dk歸一化得

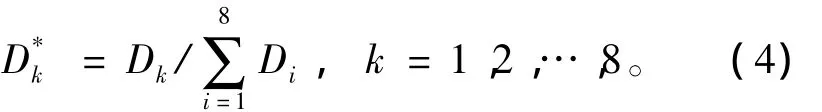
DDi為待識別樣本與一對互反的基本模式之間的歐式距離的差，如式(5)所示。

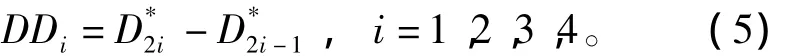
1.3 CMAC網絡模型輸出神經元的設置

板形缺陷的8種基本模式中包括4對兩兩互反的模式，根據軋制過程中軋件板形的實際情況，識別出的板形基本模式中互反的2種模式不能同時存在，因此CMAC神經網絡的輸出層采用4個輸出節點就可以準確地表達出各種基本模式的隸屬度。當輸出值為正數時，分別表示左邊浪、中浪、右三分浪和正四分浪;當為負數時，分別代表的則是右邊浪、雙邊浪、左三分浪和反四分浪。

1.4 CMAC板形識別模型

小腦模型聯接控制器CMAC神經網絡是1972年由ALBUS提出的［4］。它是一種具有局部學習能力的前饋神經網絡，其結構簡單、學習速度快，具有一定的泛化性等特點，能較好地完成非線性映射。CMAC神經網絡的基本思想在于學習系統特征的近似值，然后產生合適的控制信號［5］。CMAC神經網絡已經被成功的應用在很多領域，比如機器人控制、信號處理、模式識別等。

為了提高板形識別的精度和速度，本文提出了一種CMAC板形模式識別模型。本識別模型利用歐式距離差作為網絡的輸入，各種基本模式的隸屬度作為網絡的輸出，是一種4輸入4輸出的識別模型。這種CMAC神經網絡識別模型是一種聯想存儲網絡。其傳輸函數類似于一種查表函數。本模型是一種兩層聯想神經網絡模型［6］，其包括兩個基本的映射函數X→A和A→Ap。CMAC板形識別模型的結構如圖2所示。

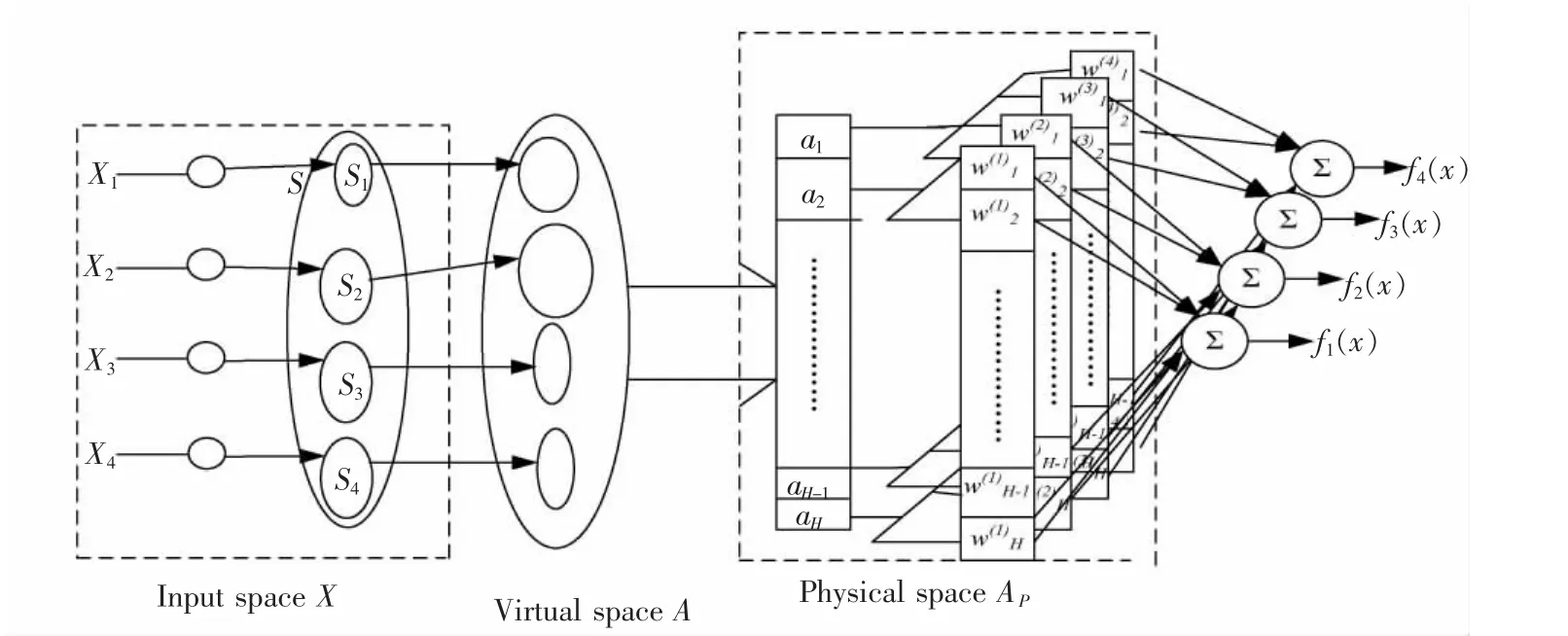
圖2 CMAC板形模式識別模型結構Fig.2 Structure of CMAC flatness recognition model

對于映射X→A，輸入空間X中的每個細胞單元首先被量化，然后分別與虛擬空間A中相對的項相聯合。在大多數多輸入的情況下，由于A會變得很大，因而不能實現網絡的功能［7-9］。因此為了壓縮虛擬空間A到一個較小的物理空間Ap，實現映射A→Ap，模型采用了哈希代碼［10-13］。

在整個映射過程中，輸入量x首先被量化到S，其量化數為R，Si是輸入量被量化的R維的量化參數。然后在物理空間Ap中，由映射得到一組相適應的權值wi(i=1，2，…，H)。CMAC網絡的輸出如式(6)所示，其中fi(x)表示輸出變量。

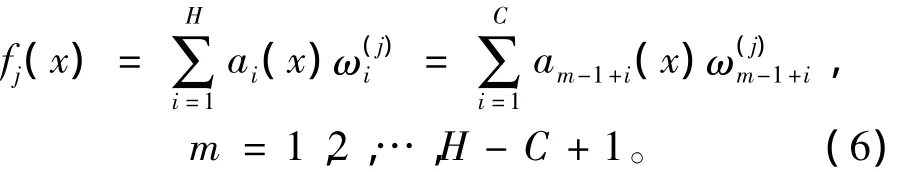
式中:fj(x)是第j個實際輸出;x為n維的輸入量;a為H維被激活的單元;C為量化參數，其表示每維輸入空間中被激活的單元數;m為被激活的存儲單元的首地址;ω(j)i表示第j個輸出的第i個存儲單元中的權值。

CMAC網絡運用誤差校正算法。其計算量小、收斂速度快。根據Widrow-Hoff規則，CMAC網絡的學習算法表示如下。

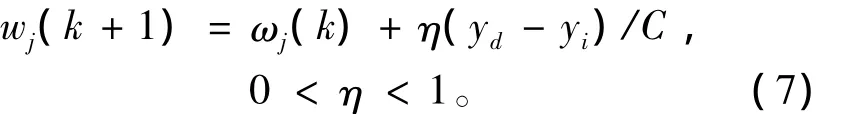
式中:k為CMAC的迭代步數;η為學習率;yd為期望輸出;(yd－yi)為訓練的誤差樣本。

1.5 CMAC模型的改進算法

CMAC網絡模型的學習率在其權值更新中起著重要的作用［14］。傳統的CMAC神經網絡具有固定的學習率，這是不合理的。若使CMAC有較大的學習率，其學習速度越快，然而其學習誤差就會更大，并且引起網絡的不穩定。相反，有較小學習率的CMAC網絡其訓練誤差較小，結果較準確，然而其學習速度較低。因此，CMAC模型中應引入動態學習率。為了獲得動態學習率，本文采用了標準誤差函數。根據此函數，動態學習率通過誤差收斂獲得。網絡模型通過變化的學習率，更新相應的權值。標準誤差函數見式(8)。

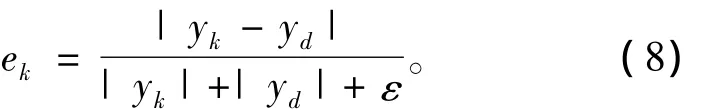
式中:k表示CMAC網絡的迭代步數;ε為任意小的正數。

通過ek得到相應的動態學習率。表示為ηk= ek。相應的權值更新函數見式(9)。

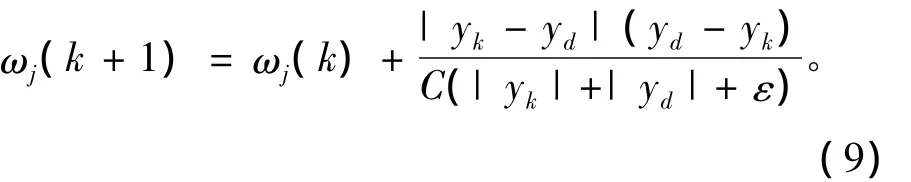
修改后的CMAC網絡模型的學習率是由每個迭代步的誤差決定的。因此此模型采用的學習率適應網絡中的每一步學習。

2 仿真實驗

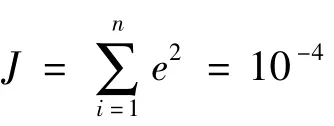
本文采用8個標準模式和69個非標準模式作為模型的輸入。表1中給出了分別利用傳統CMAC識別模型和本文提出的識別模型進行實驗后得出的結果中的9個仿真結果。

如表1所示，含有動態學習率的CMAC識別模型的識別精度比傳統的識別網絡模型明顯要高。

表2給出了3種不同的板形識別模型的比較結果。此仿真實驗中，50個模式被用做訓練樣本，25個模式被用做測試樣本。利用傳統的CMAC識別模型方法得到的MSE為0.092 9，采用本文提出的新模型MSE僅為0.070 0。

如表2所示，利用這50個樣本訓練時，方法1的訓練時間最長，其訓練時間大約是方法2的10倍。方法3的訓練時間是最短的，僅有10 s。因此，板形模式識別的精度和速度都大大得到了改進。

3 結論

本研究建立了一種新的具有動態學習率的CMAC神經網絡板形識別模型，具有如下3個特點。

1)基于勒讓德正交多項式的基模式符合實際的板形模式識別的要求。

2)采用了歐式距離差作為模型的輸入，物理意義明確，簡化了網絡結構，進一步實現了網絡結構的固定化和簡單化。此改進的板形模式識別方法可推廣到其他模式識別系統中，特別是基本模式具有兩兩互反性的模式識別系統中。

3)誤差校正算法中引入了動態學習率。同具有固定學習率的傳統方法相比較，這種方法節省了訓練時間，同時識別精度也得到了提高。

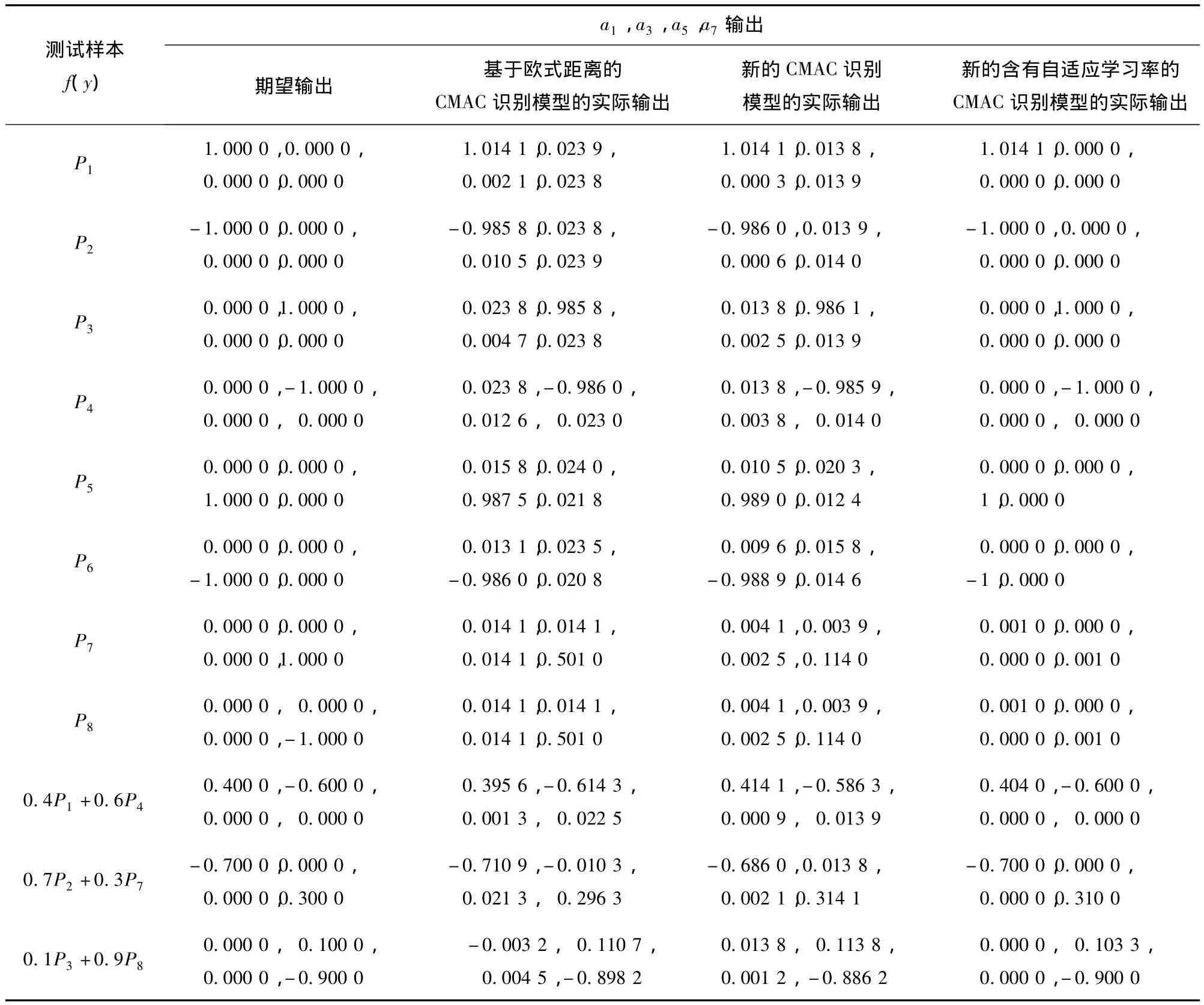
表1 3種識別模型的識別結果Tab.1 Contrast of experimental results by three recognition model

表2 3種不同板形模式識別模型的比較Tab.2 Comparison among three different models for flatness pattern recognition

/References:

［1］ 彭 艷，劉宏民.冷軋帶鋼板形檢測信號模式識別方法的進展［J］.燕山大學學報，2003，27(2):142-145.

PENG Yan，LIU Hongmin.Pattern recognition method progress of measured signals of shape in cold rolling［J］.Journal of Yanshan University，2003，27(2):142-145.

［2］ 張秀玲，劉宏民.變結構神經網絡在板形信號模式識別方面的應用［J］.鋼鐵研究學報，2001，13(2):88-92.

ZHANG Xiuling，LIU Hongmin.Pattern recognition of shape signal by variable structure neural network［J］.Journal of Iron and Steel Research，2001，13(2):88-92.

［3］ ALEKSANDER K.Basic function model of the CMAC network［J］.Neural Network，2000，12(5):107-126.

［4］ ALBUS J S.A new approach to manipulator control:The cerebellar model articulation controller(CMAC)［J］.Journal of Dynamic System Measurement and Control，1975，97:220-227.

［5］ MILLER W T，GLANZ F H，KRAFT L G.CMAC:An associative neural network alternative to backpropagation［J］.Proceedings of the IEEE，1990，78(9):1561-1567.

［6］ 張秀玲，劉宏民.板形模式識別的GA-BP模型和改進的最小二乘法［J］.鋼鐵，2003，38(10):29-34.

ZHANG Xiuling，LIU Hongmin.GA-BP model of flatness pattern recognition and improved least squares method［J］.Iron and Steel，2003，38(10):29-34.

［7］ JIA Chunyu，SHAN Xiuying，LIU Hongmin.Fuzzy neural model for flatness pattern recognition［J］.Journal of Iron and Steel Research International，2008，15(6):33-38.

［8］ PENG Y，LIU H M.A neural network recognition method of shape pattern［J］.Journal of Iron and Steel Research International，2001，8(1):16-20.

［9］ WONG Y，SIDERIS A.Learning convergence in the cerebellar model articuation controller［J］.IEEE Trans Neural Networks，1992，3(6):115-121.

［10］ 張 材，譚建平.基于遺傳算法反向傳播模型的板形模式識別［J］.中南大學學報(自然科學版)，2006，37(2):294-299.

ZHANG Cai，TAN Jianping.Strip flatness pattern recognition based on genetic algorithms-back propagation model［J］.Journal of Central South University(Science and Technology)，2006，37 (2):294-299.

［11］ WANG J.A flatness pattern recognition model based on wavelet transform and probabilistic neural network［J］.Information Computing and Applications Communications in Computer and Information Science，2012，308:187-194.

［12］ 張雪偉，王 焱.智能識別方法在板形識別中的應用及發展趨勢［J］.鋼鐵研究學報，2010，22(1):1-3.

ZHANG Xuewei，WANG Yan.Application and development trend of intelligent recognition methods for flatness recognition［J］.Journal of Iron and Steel Research，2010，22(1):1-3.

［13］ 單修迎，劉宏民，賈春玉.含有三次板形的新型板形模式識別方法［J］.鋼鐵，2010，45(8):56-58.

SHAN Xiuying，LIU Hongmin，JIA Chunyu.Analysis of a new flatness pattern recognition method containing the cubic flatness［J］.Iron and Steel，2010，45(8):56-58.

［14］ 張秀玲，趙文保，張少宇.基于改進T-S云推理網絡的板形模式識別方法［J］.中南大學學報(自然科學版)，2013，44 (2):580-586.

ZHANG Xiuling，ZHAO Wenbao，ZHANG Shaoyu.Method of flatness pattern recognition based on improved T-S cloud inference network［J］.Journal of Central South University(Science and Technology)，2013，44(2):580-586.