一類具黏性擬線性波動方程解的能量衰減和解的爆破

閆用杰， 陳翔英

(1.安康學院數學系 陜西安康725000;2.鄭州電力高等專科學校經濟貿易系 河南鄭州450004)

0 引言

研究下列初邊值問題

其中 μ ＞ 0，δ＞ 0，p≥1，q ＞ 1是常數，Ω =(0，1)，QT= Ω ×(0，T)，u(x，t)表示未知函數，σ(s)是給定的非線性函數，u0(x)和u1(x)是已知的初值函數，下標x和t分別表示對x和t求偏導數．

當μ=δ=0時的方程(1)是由文［1］作為改進的擬線性波動方程的模型引入的，此方程對于大初值存在整體光滑解．文獻［2－5］研究了方程(1)對于小初值解的整體存在性，同時研究解的漸近性質和有關的方程．當σ=μ=0和δ=1時，文［6］對于方程(1)的多維情況研究了解的漸近性質和解的衰減性質．文［7－8］證明了當δ＞0和μ＞0時，方程(1)在多維和小初值情況下整體廣義解的存在性和唯一性，但是沒有討論解的爆破．

本文的目的是給出小初值的情況下問題(1)～(3)解的能量衰減．對于大初值的情況先說明問題(1)～(3)存在唯一的局部廣義解，然后給出問題(1)～(3)解爆破的充分條件．

貫穿全文，采用下列符號:Lp(Ω)(1≤p≤∞)表示所有定義在Ω上的Lp－函數，并賦予范數 fp=fLp和 f = f2的空間;Hm(Ω)表示定義在Ω上賦予范數 fHm(Ω)的Sobolev空間，其中m≥0是一整數，Hm(QT)表示定義在Ω×(0，T)上賦予范數 fHm(QT)的Sobolev空間．

1 問題(1)～(3)的能量衰減

定理1 設文［7］中的主要定理成立，令u(x，t)是問題(1)～(3)的廣義解．若p=q=5，σ(v2)v2＞且μ＞0充分小，則成立E(t)≤C(1+t)－12，t≥0，其中C ＞0是僅依賴于E(0)的常數，

證明 根據文［8］定理8．1，只需證明問題(1)～(3)的廣義解u(x，t)是R+上的非負非增的可導函數和滿足不等式即可．為此，方程(1)兩端同乘以ut(x，t)，在Ω上積分并對x分部積分得

式(4)表示能量E(t)是非增的．因為

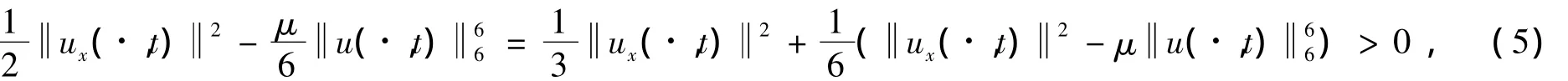
所以E(t)是非負的．式(4)對t積分有

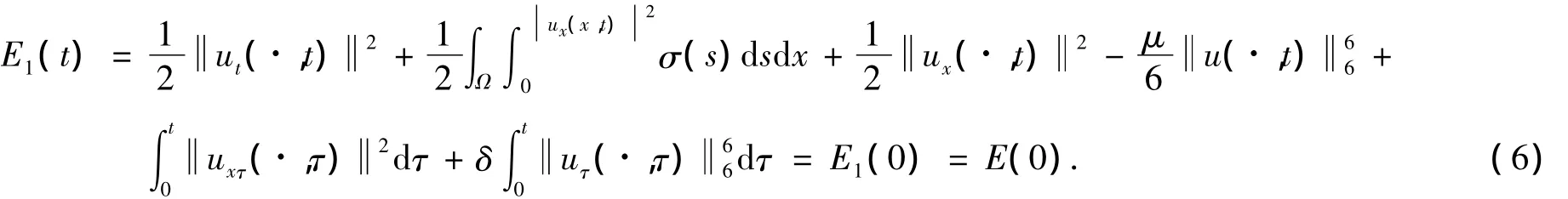
式(1)兩端乘以E2(t)u(x，t)并在Ω×(S，T)上積分，可見，

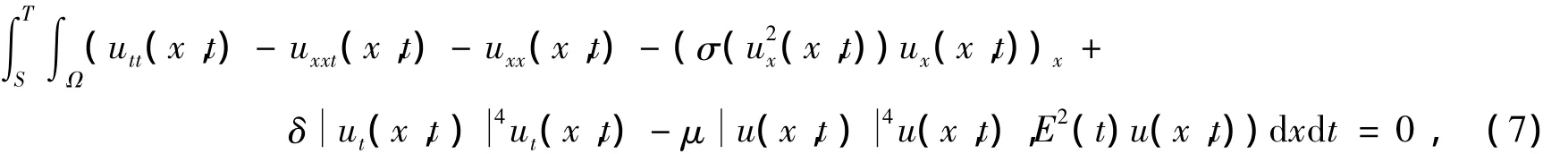
其中(，)表示L2(Ω)中的內積，0≤S＜T＜∞．對式(7)中的每一項進行估計如下:對t分部積分，得

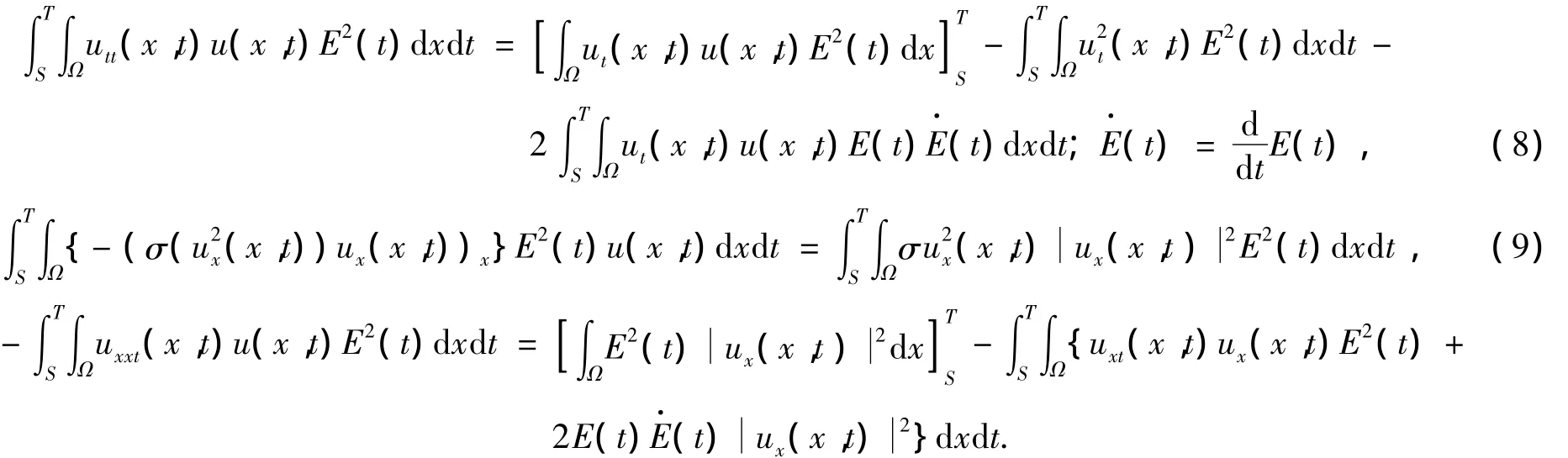
于是

將式(8)～(12)代入式(7)推出

其中，A1

由上面的估計可以得出:

其中0≤S＜T＜∞ 和Ci(i=4，5，6，7)是不依賴于S的常數．

現在估計A5．為此，首先估計B1．由式(4)推得這樣，

利用帶ε的Young不等式可見

利用H?lder不等式，帶ε＞0的Young不等式和式(4)得

其中C(ε)＞0是不依賴于S和T的常數．

利用Gagliardo-Nirenberg插值定理，由式(18)得

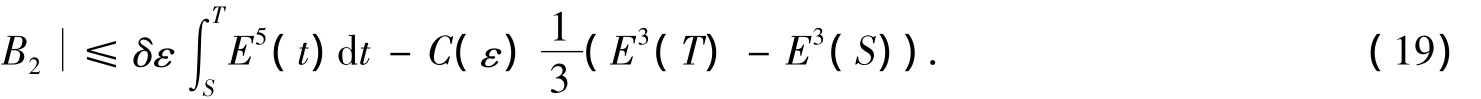
由式(17)和式(19)推出

將式(14)～(16)和式(20)～(21)代入式(13)可知

如果ε＞0選的充分小且μ＞0充分小，則存在C12＞0，使得成立．由文［8］

2 問題(1)～(3)在大初值情況下的局部廣義解和解的爆破

應用壓縮映射原理證明問題(1)～(3)存在唯一局部廣義解．

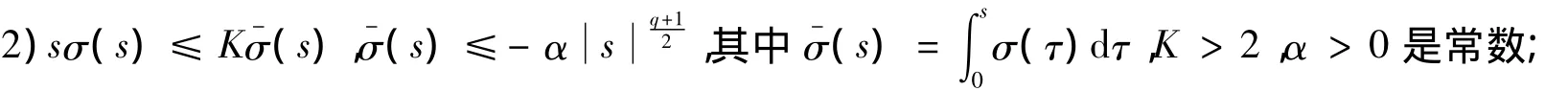
其中，

證明 式(1)的兩端同乘以2ut(x，t)并在Ω上積分，有

因此 E(t)=E(0)，t ＞ 0．令

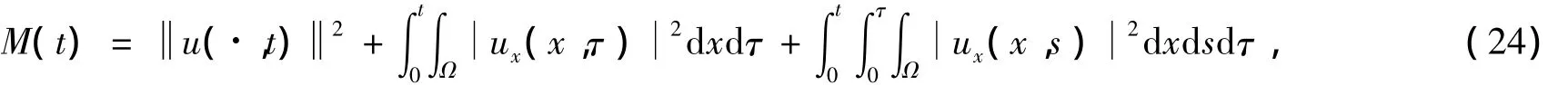
有

利用定理2的假定1)，分部積分并注意到

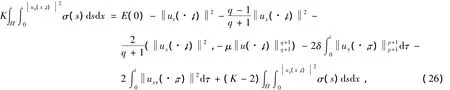
得到

應用H?lder不等式和Young不等式，可見

令c是d的共軛指數，利用前式和帶ε＞0的Young不等式可知利用Sobolev嵌入定理知

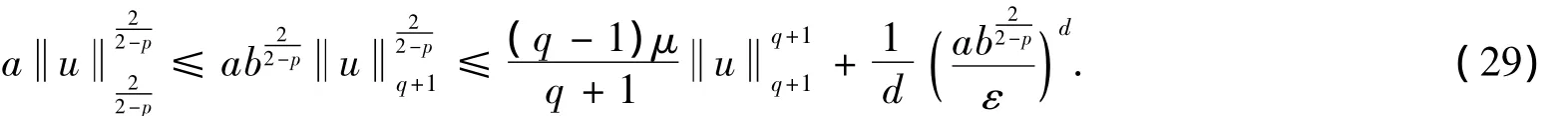
將式(29)代入式(28)得

由式(31)推出

把式(25)代入式(34)的左端，導出

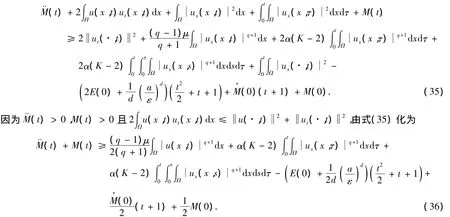
進一步縮小上式右端，發現

由式(32)和式(33)可推出當t→∞ 時，M(t)→∞ 且M(t)→∞．所以存在一個t0≥1，使得當t≥t0時，有(t)＞0和M(t)＞0．式(37)的兩端同乘以2(t)并利用式(32)得

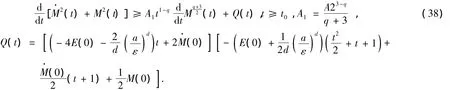
從式(38)可得

式(39)在(t0，t)上積分，有

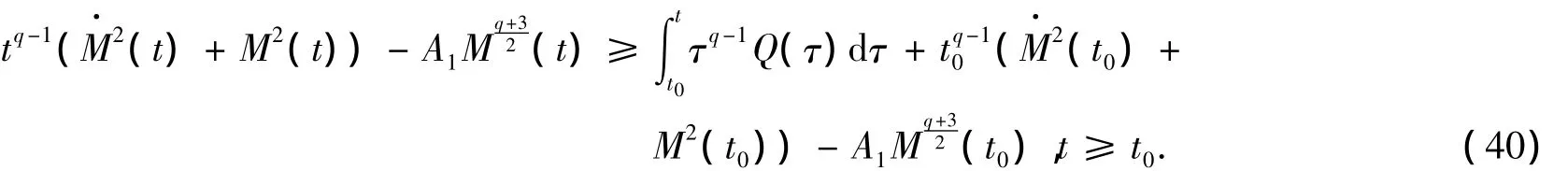
可以看出，當t→∞ 時，式(40)的右邊趨于∞，因此存在一個t1≥t0，使得當t≥t1時，式(40)右端大于或等于0，因此推出

致謝:此文是在鄭州大學陳國旺教授的指導下完成的，特此對他表示感謝!

［1］ Greenberg J M.On the existence，uniqueness and stability of the equation ρXtt=E(Xx)Xxx+Xxxt［J］.J Math Anal Appl，1969，25:575-591.

［2］ Kawashima S，Shibata Y.Global existence and exponential stability of small solutions to nonlinear viscoelasticity［J］.Comm Math Phys，1992，148:189-208.

［3］ Mizohata K，Ukai S.The global existence，uniqueness of small amplitude solutions to the nonlinear acoustic wave equations［J］.J Math Kyoto Univ，1993，33:505-522.

［4］ Matsuyama T，Ikehata R.On global solutions and energy decay for the wave equations of Kirchhoff type with nonlinear damping terms［J］.J Math Anal Appl，1996，204:729-753.

［5］ Nakao M.Energy decay for the quasi-linear wave equation with viscosity［J］.Math Z，1995，219:289-299.

［6］ Nakao M.On strong solutions of the quasilinear wave equation with viscosity［J］.Adv Math Sci Appl，1996，6:267-278.

［7］ Chen Guowang，Wang Yanping.A note on“On the existence of solutions of quasi-linear wave equations with viscosity”［J］.Nonlinear Analysis TMA，2008，68:609-620.

［8］ Komonik V.Exact Controllability and Stabilization［M］.Paris:Masson-John Wiley，1994.

［9］ Mazja Vladimir G.Sobolev Spaces［M］.New York:Springer-Verlag，1985.

［10］ Chen Guowang，Yue Hongyun，Wang Shubin.The initial boundary value problem for quasi-linear wave equation with viscous damping［J］.J Math Anal Appl，2007，331:823-839.