欠熱沸騰模型參數敏感性分析

郜 冶，李小暢，劉平安

（哈爾濱工程大學 航天與建筑工程學院，黑龍江 哈爾濱 150001）

近十年來，基于歐拉-歐拉兩流體六方程模型的RPI（Rensselaer Polytechnic Institute）欠熱沸騰數值模型［1］得到了較大的發展，越來越多地應用于反應堆工程熱工水力研究［2-3］。然而，由于沸騰機理尚不十分明確，現有的基于RPI模型的欠熱沸騰數值計算方法主要建立在眾多經驗或半經驗封閉子模型的基礎上，這些子模型適用范圍有限，且模型參數無通用確定方法，因此，對工況的依賴性較大。封閉子模型中的氣泡脫離壁面直徑、氣泡脫離頻率及成核面密度模型關系到氣泡份額和壁面溫度等重要熱工參數計算結果的準確性。許多學者針對不同實驗工況及流動工質提出了不同的封閉子模型，但均缺乏普適性［4］。另外，氣泡脫離壁面后的運動主要受氣液兩相間相互作用力影響，氣泡的運動反過來又會影響近壁面氣泡份額和換熱效率，因此兩相間相互作用力模型同樣十分重要。可見基于現有模型研究各封閉子模型及相間作用力模型的具體影響方式對正確使用RPI模型進行數值計算意義重大。

本文基于Nylund等［5］的FT-6a實驗，研究3個重要封閉子模型（氣泡脫離壁面直徑、氣泡脫離頻率及氣泡成核面密度）及兩個重要相間非曳力模型（升力和湍流耗散力）對氣泡軸向及徑向分布和壁面過熱度等計算結果的影響方式。

1 數學模型

RPI欠熱沸騰數值計算方法基于歐拉-歐拉兩流體六方程模型、壁面熱流量分區模型及相間傳輸模型。本文主要給出壁面熱流量分區模型及相間傳輸模型，歐拉-歐拉兩流體六方程模型作為最基本的守恒方程本文不再給出。

1.1 壁面熱流量分區模型

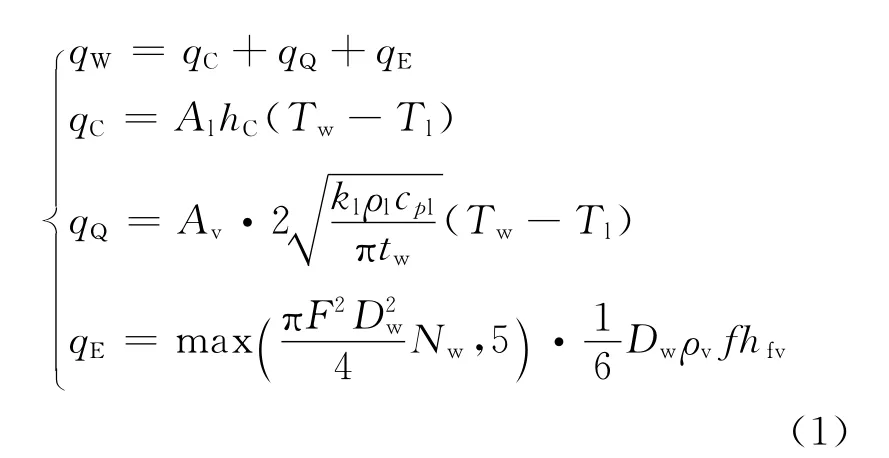
Kurul等［1］提出的RPI模型的核心機理是基于Judd等［6］的實驗和理論研究：通道內發生壁面沸騰時可將壁面熱流量分為單相對流傳熱、蒸發傳熱及氣液置換傳熱3部分。壁面熱流量分區模型基本方程如下：式中：qW、qC、qQ和qE分別為壁面總熱流量、單相對流傳熱量、氣液置換傳熱量和蒸發傳熱量；hC為單相對流換熱系數，通過壁面函數求解；Tw、Tl分別為壁面溫度與近壁面液相溫度；kl、ρl、cpl分別為液相導熱系數、密度與比定壓熱容；tw、f 分 別 為 氣 泡 脫 離 周 期 與 頻 率；ρv 為 氣相密度；F 為氣泡對壁面的影響因子，取值為2；Nw為壁面成核面密度；Dw為氣泡脫離壁面直徑；Av、Al分別為壁面上氣相與液相的單位覆蓋面積，Av=min（1，πF2DwNw／4），Al=1-Av；hfv為汽化潛熱。由于該模型在計算中將氣相溫度固定為系統壓力下的飽和溫度，因此僅適用于氣泡體積分數較低（αmax＜0.8）的情況。

式（1）中氣泡脫離壁面直徑、氣泡脫離頻率及壁面成核面密度未知，需要相應子模型對其進行封閉，本文選用如下使用相對較為廣泛的模型［7］：

式中：Tsub、Tsup分別為液相欠熱度和壁面過熱度，Tsup=Tw-Tsat，Tsub=Tsat-Tl；Tref為參考溫度；Dref為氣泡脫離壁面參考直徑；Nref為壁面成核參考面密度；Cf為氣泡脫離阻力因子；Dmax為氣泡脫離壁面時的最大直徑。式（2）中多處涉及近壁面液相溫度，為減小對近壁面網格的依賴，本文取y+=250時第1層網格節點上的液相溫度。

1.2 相間傳輸模型

1）質量傳輸

氣液兩相間的質量傳輸包括過熱壁面上的汽化和主流區的蒸發或冷凝。過熱壁面上液相的汽化速率可由式（1）中的蒸發傳熱量得到：

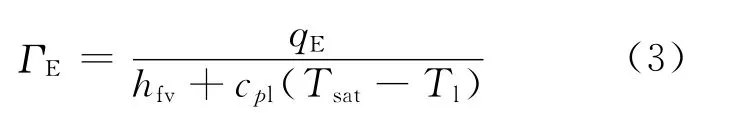
氣泡脫離壁面后在主流區的蒸發和冷凝速率如下：

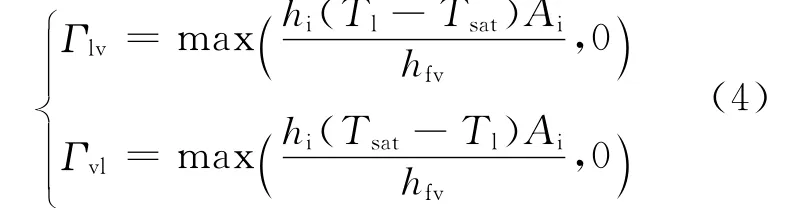
式中：Гlv、Гvl分別為蒸發和冷凝速率；Ai為相界面積，根據氣泡直徑Db求解；hi為相界面換熱系數，根據Ranz-Marshall關系式獲得［8］。

2）能量傳輸

氣液兩相間的能量傳輸以相界面作為參考，兩相間的熱量傳輸為：

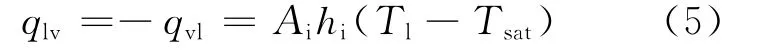
式中，qlv與qvl分別為液相向氣相傳熱量及氣相向液相傳熱量，二者大小相同，正負相反。

3）動量傳輸

兩相間動量傳輸用相互作用力表示，流動沸騰中總的相互作用力FT包括曳力FD和非曳力FND兩類，其中非曳力又包含升力FL、湍流耗散力FTP及壁面潤滑力FWL：

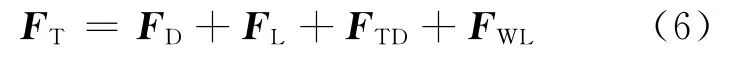
各相互作用力的求解模型為：

式中：CD為曳力系數，由Ishii-Zuber關系式確定［9］；v為速度矢 量；Δ為哈密頓算子；Db為氣泡直徑；CL為升力系數；yw為壁面法向距離；Cw1、Cw2為 無 量 綱 參 數，分 別 取-0.01 和0.05［10］；FTD，Favre、FTD，Lopze分別為湍流耗散力 的Favre平 均 模 型［11］和Lopze模 型［12］，其 中CD與曳力模型相同，CTD為湍流耗散系數；νt、σt分別為液相湍流黏性系數及湍流Schmidt數；kl為液相湍流動能。

4）氣泡直徑及相界面積

本文采用Kurul等［1］推薦的基于當地液相欠熱度氣泡直徑模型：

基于該氣泡直徑模型，相界面積則可采用如下對稱模型獲得：

2 數值計算方法

數值計算基于ANSYS CFX 14.5軟件包，該程序提供了歐拉-歐拉兩流體六方程模型框架，在加熱壁面邊界條件的處理中嵌入了RPI模型，并提供了部分相間傳輸模型，未提供的模型可利用User Fortran以源項的形式加入到守恒方程中。

本文以Nylund等［5］的FT-6a實驗為研究對象，實驗模型及尺寸參數如圖1a所示。實驗以水為工質，系統壓力為5.0MPa，入口欠熱度為4.5K，入口流量為1 163kg／（m2·K），均勻壁面熱流量為522kW／m2。取實驗模型周向的1／10和軸向加熱段前2m 作為數值計算對象，如圖1a中陰影部分所示。氣相物性參數取系統壓力下的飽和蒸汽參數；液相則取進出口的平均值。液相湍流模擬采用k-ω SST 模型［13］，氣相則采用零方程模型。計算中建立了3套網格：286×50、391×100、605×200，各網格計算的平均氣泡份額差值小于3%，選取第2套網格作為計算對象，如圖1b所示。

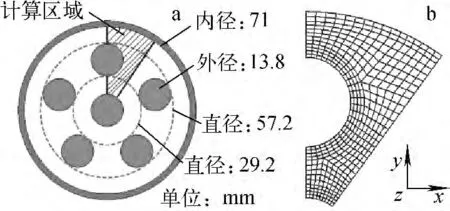
圖1 FT-6a幾何模型及計算網格Fig.1 Sketch of FT-6ageometry and computational mesh

3 計算結果分析

分析RPI模型中3 個子模型（Dw、Nw及f）及兩個相間非曳力模型（FL及FTD）對計算結果的影響。從式（1）及（2）可看出，RPI模型主要由Dw、Nw及f 確定，對于一具體的流動沸騰，這些封閉子模型主要由式（2）中的Dref、Cf及Nref決定。從式（7）則可看出，升力主要受升力系數CL影響，Favre湍流耗散力模型參數CD已由曳力模型確定，Lopze湍流耗散力模型則主要受耗散系數CTD影響。因此，針對上述所選定的RPI封閉子模型及相間非曳力模型的研究可通過分析如下5個參數對數值計算結果的 敏 感 性 來 實 現：Dref、Cf、Nref、CL及CTD。根據文獻［7］，5個參數推薦值列于表1。

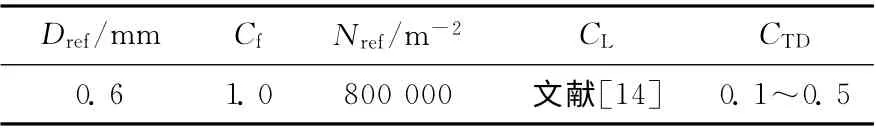
表1 模型參數參考值Table 1 Reference values of model parameters

FT-6a實驗測量了氣泡沿軸向和徑向的分布，未給出壁面過熱度，本文采用Jens 關聯式［15］估算充分發展的欠熱流動沸騰壁面過熱度：

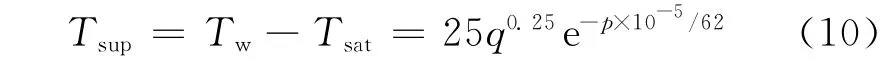
式中：q 為 壁 面 熱 流 量，MW／m2；p 為 系 統 壓力，Pa。基于式（10）所計算的FT-6a實驗壁面過熱度為9.49K。另外，Bartolomej等［16］基于圓管的類似工況（4.5 MPa，0.57 MW／m2）下的欠熱沸騰實驗結果約為10K，因此可基本確定Jens關聯式計算結果的準確性。

3.1 子模型參數敏感性分析

計算時升力及湍流耗散力分別采用Tomiyama和Favre模型，其他子模型參數取表1中的值。圖2為Dref對軸向平均氣泡份額及壁面過熱度的影響。從圖2可看出，隨參考直徑的增大，平均氣泡份額逐漸增大，壁面過熱度則隨之降低。這是由于隨壁面氣泡直徑的增大，蒸發傳熱量及氣液置換傳熱量隨之增大，由蒸發傳熱產生的氣泡份額增加，此時傳熱效率升高，壁面溫度降低。參考直徑達1.3mm 時，平均氣泡份額與實驗結果符合較好，但壁面過熱度大幅低于Jens關聯式計算值，參考直徑取0.9mm 時壁面過熱度與關聯式符合較好。該圖表明Dw對平均氣泡份額和壁面溫度的計算結果影響均較大。

圖3示出Nref對平均氣泡份額及壁面過熱度的影響。圖3表明，隨Nref的增大，氣泡份額逐漸增大，壁面過熱度則隨之減小。顯然這與物理事實相符，壁面成核點越多，氣泡產生量越多，傳熱效率提高，壁面溫度降低。當Nref＞8×105m-2時，計算結果不再變化，這是由于式（1）中的qE受max函數限制。在Nref的有效影響范圍內，成核面密度對氣泡份額及壁面溫度影響均較明顯。

圖4為Cf對平均氣泡份額及壁面過熱度的影響。從圖4 可看出，當減小阻力因子時（＜1），該參數對氣泡份額的計算結果幾乎無影響，對壁面過熱度的影響也較小。當增大阻力因子時（＞1），氣泡份額有所下降，壁面過熱度則大幅升高。

圖2 Dref對軸向平均氣泡份額及壁面過熱度的影響Fig.2 Influence of bubble departure diameter on axial average void fraction and wall superheat

圖3 Nref對平均氣泡份額及壁面過熱度的影響Fig.3 Influence of wall nucleation site density on axial average void fraction and wall superheat

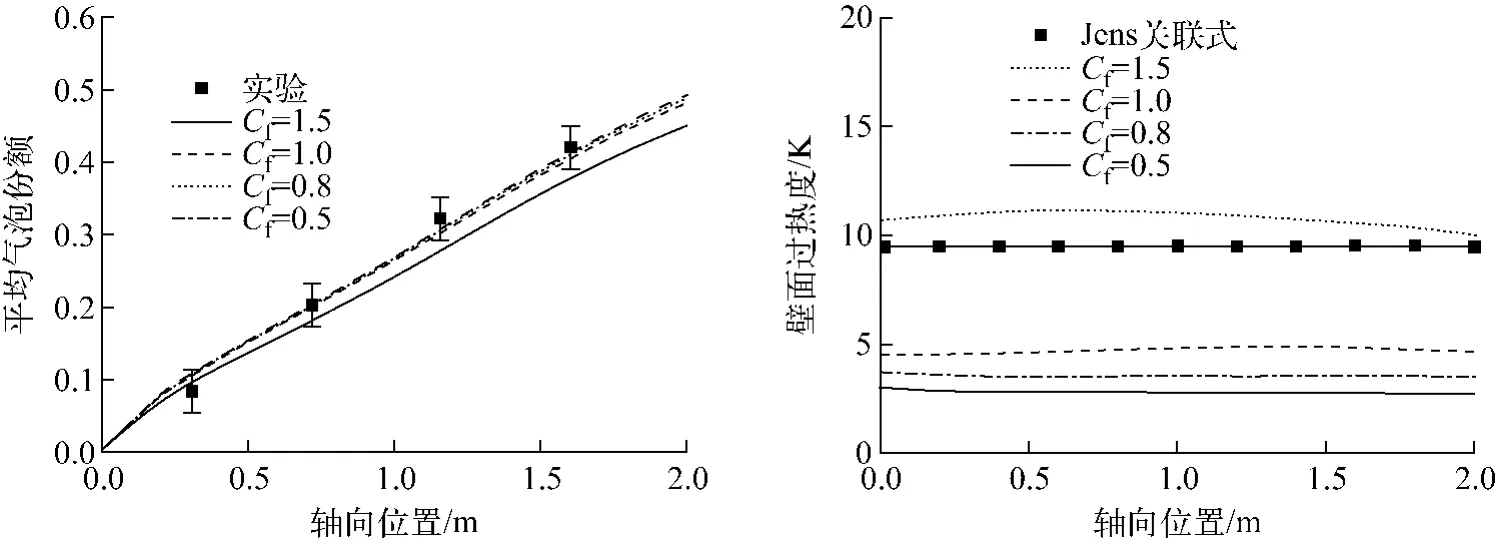
圖4 Cf 對平均氣泡份額及壁面過熱度的影響Fig.4 Influence of bubble detachment frequency on axial average void fraction and wall superheat

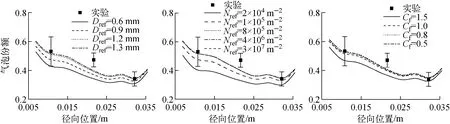
圖5 RPI子模型對線平均氣泡份額徑向分布的影響Fig.5 Influence of RPI sub-models on radial distribution of line-averaged void fraction

圖5為RPI各子模型計算的線平均氣泡份額在1 598mm 高處徑向分布與實驗結果的對比。從圖5可看出，合適的模型參數可得到與實驗數據基本一致的計算結果。圖中各曲線基本平行說明各封閉子模型對氣泡的徑向分布無任何影響，只影響氣泡份額大小。

綜合上述，脫離壁面氣泡直徑及成核密度對氣泡份額及壁面過熱度計算結果影響相對較大，氣泡脫離頻率對二者的影響相對較小。不能單獨對比某一參數的實驗值來確定計算結果的可靠性。對于FT-6a 實驗，推薦參考直徑0.9mm，參考成核面密度8×105m-2，氣泡脫離頻率阻力因子1.0。

3.2 非曳力模型參數敏感性分析

通過氣泡徑向分布計算結果來分析非曳力模型參數敏感性。圖6為采用不同升力系數計算得到的氣泡徑向分布與實驗結果的對比。從圖6可看出，不同升力系數主要影響棒束間隙（0.01m）及絕熱壁面附近（0.035m）氣泡份額大小。升力系數越大，棒束間隙處氣泡份額越小，絕熱壁面附近氣泡份額越大。Tomiyama關系式與實驗符合較好，CL取0.5 時與Tomiyama關系式的計算結果接近。

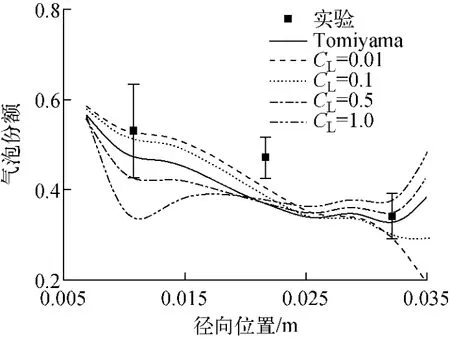
圖6 升力系數敏感性分析Fig.6 Sensitivity analysis of lift coefficient

圖7為不同湍流耗散力模型計算結果與實驗結果的對比。從圖7可看出，與升力不同，湍流耗散力主要影響加熱壁面附近氣泡份額大小。從Lopez模型可看出，湍流耗散系數越大，加熱壁面附近氣泡份額越小。這意味著湍流耗散力有促進氣泡遠離加熱壁面的作用。Favre模型與CTD取0.5時的Lopez模型計算結果接近，且與實驗數據符合較好。

圖7 湍流耗散力模型敏感性分析Fig.7 Sensitivity analysis of turbulent dispersion force

為進一步觀察相間非曳力模型對氣泡徑向分布的影響，圖8示出了1 598 mm 截面處升力及湍流耗散力對氣相分布的影響。從圖8a可看出，CL較小（0.01）時，氣泡更多地向主流區運動；CL較大（1.0）時，氣泡被束縛在壁面附近，Tomiyama模型計算的結果則處于二者之間。圖8b表明，CTD較小（0.1）時，氣泡聚集在壁面附近；CTD較大（0.5）時，氣泡則向主流區擴散。分析結果與圖7基本一致。

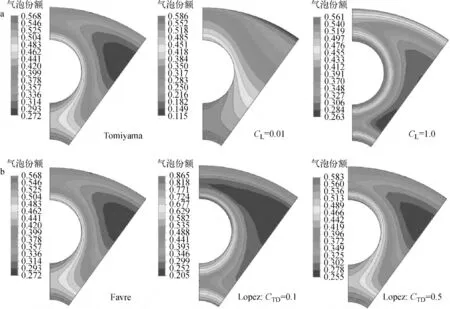
圖8 升力（a）及湍流耗散力（b）對氣相分布的影響Fig.8 Influence of lift force（a）and turbulent dispersion force（b）on void fraction contours

4 結論

1）氣泡脫離壁面直徑模型對氣泡份額及壁面溫度的計算影響均較大，隨壁面氣泡直徑的增大，氣泡份額增加，壁面溫度降低。

2）成核面密度在其有效影響范圍內對壁面過熱度的影響較大，對氣泡份額相對較小。成核面密度越大，氣泡份額越大，壁面過熱度越低。

3）對氣泡脫離頻率而言，當氣泡脫離阻力因子在小于1的范圍內變化時，對氣泡份額的計算結果幾乎無影響，對壁面過熱度的影響也較小；當阻力因子大于1時，則對二者的影響均較大。

4）各RPI封閉子模型對氣泡徑向分布無任何影響，只影響氣泡份額大小。

5）不能通過對比單個參數的實驗測量值來驗證計算的可靠性，應綜合對比多個實驗值，以確定最佳模型參數。

6）相間非曳力模型對氣泡徑向分布的計算影響較大，升力有阻止氣泡離開加熱壁面的作用，湍流耗散力有促進氣泡向主流區運動的作用。

本文可為今后改善欠熱沸騰數值計算的準確性在模型及參數選取方面提供參考。

［1］ KURUL N，PODOWSKI M Z.On the modeling of multidimensional effects in boiling channels［C］∥27th National Heat Transfer Conference.USA：ANS，1991：28-31.

［2］ LO S，OSMAN J.CFD modeling of boiling flow in PSBT 5×5bundle［J］.Science and Technology of Nuclear Installations，2012（1）：1-8.

［3］ 李小暢，郜冶.壓水堆子通道欠熱沸騰數值驗證及交混翼研究［J］.原子能科學技術，2013，47（12）：2 208-2 215.LI Xiaochang，GAO Ye.Numerical validation of subcooled boiling in subchannel of PWR and Research on mixing vane［J］.At Energy Sci Technol，2013，47（12）：2 208-2 215（in Chinese）.

［4］ CHEUNG S C P，VAHAJI S，YEOH G H，et al.Modeling subcooled flow boiling in vertical channels at low pressures，Part 1：Assessment of empirical correlations［J］.International Journal of Heat and Mass Transfer，2014，75（1）：736-753.

［5］ NYLUND K M，BECKET R，EKLUND O，et al.Measurements of hydrodynamics characteris-tics，instability thresholds，and burnout limits for 6-rod clusters in natural and forced circulation［R］.Sweden：FRtGG-I，1967.

［6］ JUDD R L，HWANG K S.A comprehensive model for nucleate pool boiling heat transfer including microlayer evaporation［J］.ASME J Heat Transfer，1976，94（4）：623-629.

［7］ KREPPER E，KONCAR B，EGOROV Y.CFD modeling of subcooled boiling concept，validation and application to fuel assembly design［J］.Nucl Eng Des，2006，237（7）：716-731.

［8］ RANZ W E，MARSHALL W R.Evaporation from drops［J］.Chem Eng Prog，1952，48（4）：173-180.

［9］ ISHII M，ZUBER N.Drag coefficient and relative velocity in bubbly，droplet or particulate flows［J］.AIChE Journal，1979，25（5）：843-855.

［10］ANTAL S P，LAHEY R T，FLAHERTY J E.Analysis of phase distribution in fully developed laminar bubbly two-phase flow［J］.Multiphase Flow，1991，17（5）：635-652.

［11］BURNS A D B，FRANK，T，HAMILL I，et al.The Favre averaged drag model for turbulent dispersion in Eulerian［C］∥5th International Conference on Multiphase Flow.Yokohama，Japan：ICMF，2004：1-17.

［12］LOPEZ D B.Turbulent bubbly flow in a triangular duct［D］.New York：Rensselaer Polytechnic Institute，1991.

［13］KONCAR B，KREPPER E，EGOROV Y.CFD modeling of subcooled flow boiling for nuclear engineering applications［C］∥International Conference of Nuclear Energy for New Europe.Bled Slovenia：NSS，2005：1-14.

［14］TOMIYAMA A，TAMAI H，ZUN I，et al.Transverse migration of single bubbles in simple shear flows［J］.Chem Eng Sci，2002，57（11）：1 849-1 858.

［15］JENS W H，LOTTES P A.Analysis of heat transfer，burnout，pressure drop and density data for high pressure water，ANL-4627［R］.Michigan：ANL，1951.

［16］BARTOLOMEJ G G，CHANTURIYA V M.Experimental study of true void fraction when boiling subcooled water in vertical tubes［J］.Thermal Engineering，1967，14（2）：123-128.