基于約束的MLEM 圖像重建算法

張 斌，王 英，艾憲蕓，魏 星

（防化研究院 國民核生化災害防護國家重點實驗室，北京 102205）

編碼孔γ相機作為一種新型的核輻射監測設備，能通過生成可視化圖像使操作人員快速識別并定位視野中放射源目標，可極大縮短作業時間，減少人員受到的照射劑量，在環境輻射監測、核廢料處理、通關口岸貨物放射性檢測等領域具有廣泛應用。與普通光學相機不同的是，編碼孔γ相機并不能直接對放射性物質進行成像，而要在成像過程中進行所謂的“編碼”和“解碼”：放射源發射出的γ射線經過編碼孔準直器調制后在探測器上形成投影圖像，經過離散采樣后傳入計算機中，再通過特定圖像重建算法恢復出可視化的放射性強度二維分布圖像。線性算法和迭代算法是編碼孔γ相機圖像重建中的兩類主要算法。線性算法如交叉相關法［1］等具有算法簡單、計算速度快的優點，但在投影圖像受噪聲影響較大的情況下重建圖像質量較差。以MLEM 算法為代表的迭代算法能很好地抑制噪聲，對不完全數據亦能重建，然而MLEM 算法的缺點是收斂速度慢，且在投影圖像中包含噪聲較大時，迭代次數過高會使重建圖像中噪聲隨迭代次數的增加而加劇。針對這種情況，本文將直接解調法（direct demodulation method）［2］思想應用于MLEM 算法中，在迭代過程中加入先驗物理約束條件，并以交叉相關法計算結果作為迭代初始值，加快MLEM迭代的收斂速度，提高重建圖像的質量。

1 算法介紹

1.1 二維MLEM 算法

極大似然估計法是根據極大似然準則來求解似然函數中未知參數的一種參數估計法，解決這類問題的基本方法是求偏導解方程，但在圖像重建中，未知參數眾多，計算如此繁復的方程組幾乎是不可能的。用期望最大化法實現極大似然圖像重建最早由Shepp等［3］于1982年提出，最終形成MLEM 算法。期望最大化法以迭代法為基礎，通過迭代更新方程組中參數的估計值，使似然函數不斷增大，直至逼近其最大值，最終獲得極大似然參數的估計值，這樣就把原本極其復雜的極大似然估計問題轉化為簡單的求解期望值最大化過程。MLEM 算法是一種基于泊松統計模型的貝葉斯后驗概率最大的圖像復原方法，該算法以符合實際情況的模型為基礎，重建圖像的分辨率和本底噪聲抑制能力較傳統線性算法提升很多，因此在核醫學等領域得到了廣泛應用。編碼孔γ相機圖像重建中的二 維MLEM 算 法［4］可 表 示 為：

式中：“＊”表示卷積運算；“?”表示相關運算；fk（x，y）為第k次迭代后的圖像估計值；p（x，y）為γ射線透過編碼板后在探測器上的實際投影圖像；h（x，y）為編碼函數。

1.2 基于約束的MLEM 算法（DD-MLEM）

在理想無噪聲的情況下，MLEM 迭代的解是收斂的，重建出的圖像與目標圖像最終趨于一致。但實際成像中所測得的投影圖像數據中必然包含有各種噪聲，這使得迭代不能完全收斂：在迭代次數較低時，圖像質量逐漸提高；當迭代次數超過某一值后，圖像質量反而變差。這主要是因為MLEM 迭代的修正準則是要求投影估計值與實測投影越接近越好，但對于重建出的圖像卻無任何約束。為改善MLEM 迭代在實際使用中的收斂性，本文借鑒了直接解調法思想來優化MLEM算法，提高重建圖像質量。直接解調法最初是一種應用于高能射線天文望遠鏡中的成像方法，該方法與其他算法的顯著區別是利用先驗的物理知識作為約束條件，并添加到迭代求解的過程中。在迭代過程中加入的物理約束是對于被測目標的已知信息，所以使用這種方法不僅能有效抑制投影數據中本底噪聲的影響，使迭代收斂性得到明顯改善，而且最終重建出的圖像較單純使用MLEM 算法能更加趨近于真實情況。

實際成像的圖像重建過程中主要使用本底約束條件：若fk（x，y）＜fb（x，y），則令fk（x，y）＝fb（x，y），其中fb（x，y）為本底約束值。如果本底噪聲水平較低，可選擇fb（x，y）＝0；如果本底噪聲較強，為了提高成像靈敏度，需先得到背景輻射強度分布db，db可取估計值或由實際觀測數據中剔除放射源影響后獲取，然后再求解調制方程Hfb＝db（H 為系統的傳遞函數），最終得到迭代的本底約束fb。

此外，在進行圖像重建迭代時，一般選擇均勻的灰度圖像作為迭代的初始值，本文仿真中采用了交叉相關法的重建結果作為迭代的初始值，實驗證明這種方法可在一定程度上加快迭代收斂速度。交叉相關法的計算過程可由下式表示：

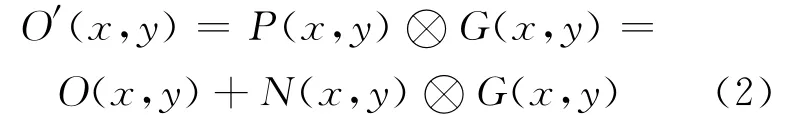
其中：O′（x，y）為對放射源目標O（x，y）的估計圖像；P（x，y）為投影圖像；G（x，y）為解碼函數（由成像系統的編碼函數決定）；N（x，y）為噪聲項。

由此，本文中基于約束的MLEM 算法計算過程可分為以下幾個步驟：

1）令k＝0，初始化fk（x，y）（一般將初始化圖像f0（x，y）設置為各像素相等的均勻灰度圖像，本文中將其設置為交叉相關法的重建圖像）；

2）應用式（1）計算fk＋1（x，y）；

3）對fk＋1（x，y）施加一定的物理約束條件；

4）根據一定的準則判斷迭代重建結果是否達到收斂要求，若已達到要求，則停止迭代；若未達到要求，則令k＝k＋1，將更新后的fk（x，y）再次轉入執行步驟2。

2 仿真實驗與分析

2.1 仿真條件

仿真實驗以19×19的改良均勻冗余陣列（modified uniformly redundant array，MURA）編碼孔準直器為基礎，成像系統參數選擇為：物距500mm，像距80mm，編碼板小孔單元邊長2mm，編碼板厚度5mm，材料為鎢。探測目標為位于視野中心軸線上的1 個點源，活度為1 MBq，能量為662keV。由上述條件模擬的理想點源圖像和投影圖像如圖1所示。迭代時在模擬投影圖像中加入隨機高斯噪聲，得到含噪聲的投影數據進行圖像重建。

2.2 評價準則

在對比兩種算法重建圖像的效果時，有時通過主觀觀察很難判斷，為了驗證所提出方法的有效性，采用歸一化均方誤差（normalized root mean square error，NRMSE）衡量算法的收斂速度，用相關系數（correlation coefficient，CC）評價重建圖像的質量，它們的定義［5］分別為：

式中：xij和分別為真實圖像和重建圖像的像素灰度值和分別為真實圖像和重建圖像的平均像素灰度值。歸一化均方誤差表示重建圖像與真實圖像的接近程度，其值越小代表重建效果越好，而相關系數評價的是重建圖像與真實圖像的相似度，其值越大表示重建圖像與真實圖像越接近。

圖1 模擬的點源圖像和投影圖像Fig.1 Simulated point source image and projection image

2.3 仿真結果分析

在實際成像中，當成像系統計數率足夠高時，投影圖像中疊加的噪聲趨近于高斯分布。仿真實驗采用了這一噪聲模型，在DD-MLEM迭代中構造基于高斯分布的本底并進行圖像重建，將重建后的背景圖像作為迭代約束條件，采用交叉相關法計算結果作為迭代初值。圖2和圖3分別為MLEM 算法和DD-MLEM 算法迭代次數n＝30、90、270時的重建圖像。通過直接觀察可看出，在選取合適迭代次數的情況下，兩種算法均能得到相對較好的重建效果，但在迭代次數過高時，MLEM 算法重建的圖像局部區域噪聲被放大，原本光滑的圖像出現離散的斑點，在視覺上難以接受；而DD-MLEM 迭代則不然，在過高迭代次數下依然能很好地控制圖像噪點，保持圖像的可辨識性。

圖2 MLEM 迭代重建圖像Fig.2 Reconstructed image by MLEM iteration

圖3 DD-MLEM 迭代重建圖像Fig.3 Reconstructed image by DD-MLEM iteration

為進一步評價重建圖像的質量，利用式（3）和式（4）給出的評價準則對兩種算法的重建圖像效果進行定量分析。圖4示出兩種算法所重建圖像的歸一化均方誤差隨迭代次數的變化情況。由圖4a可看出，在迭代次數相對較低時，兩種算法的歸一化均方誤差均隨迭代次數的增加而減小，重建圖像質量不斷提高，但DD-MLEM算法的收斂速度顯然要快得多；當迭代次數繼續增加時，由圖4b可知，MLEM 算法的歸一化均方誤差在達到一最小值后迅速增大，重建圖像的質量也隨之變差，而DD-MLEM 算法在迭代次數過高的情況下歸一化均方誤差只是略微變大，重建圖像的質量仍能保持得比較好。圖5示出兩種算法的相關系數隨迭代次數的變化情況，可更加明顯地看出DD-MLEM 算法收斂速度不但更快，而且提高了算法最佳迭代次數，重建圖像的質量也優于原算法。在迭代次數過高時，MLEM迭代的重建圖像質量迅速下降，而DD-MLEM 迭代則能將圖像質量一直保持在較高水平上。

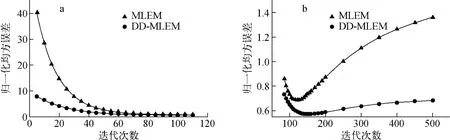
圖4 歸一化均方誤差隨迭代次數的變化Fig.4 NRMSE of two algorithms versus iteration time

圖5 相關系數隨迭代次數的變化Fig.5 CC of two algorithms versus iteration time

3 結論

在編碼孔γ相機圖像重建中，MLEM 迭代算法能較為有效地抑制統計噪聲，較傳統交叉相關法恢復出的圖像質量要高得多，但缺點是收斂速度較慢且迭代次數過高時圖像質量變差。本文提出一種基于約束的MLEM 算法，在迭代過程中加入物理約束條件，并用交叉相關法計算值作為迭代初始值。實驗結果證明，DD-MLEM 算法不僅收斂速度加快，且重建圖像質量和迭代的收斂性與收斂速度均得到顯著提高。使用這種方法可更加充分地利用被觀測目標的已知信息，從而有效抑制由于噪聲等因素所引起的迭代解的病態特征，相比僅用迭代法或相關法能更好地重建出反映真實情況的圖像。值得注意的是，此方法重建圖像的質量對約束條件有較強的依賴，對于復雜的測量環境，應根據現場實際情況選取更為合理的物理約束條件以保證成像質量。

［1］ 何會林，董永偉，吳伯冰，等.空間硬X 射線編碼孔成像望遠鏡樣機的研制及初步實驗結果［J］.高能物理與核物理，2007，31（5）：437-441.HE Huilin，DONG Yongwei，WU Bobing，et al.A prototype of spatial hard X-ray coded aperture imaging telescope and the primary laboratory experimental results［J］.High Energy Physics and Nuclear Physics，2007，31（5）：437-441（in Chinese）.

［2］ 李惕碚，吳枚.高能天文中成像和解譜的直接方法［J］.天體物理學報，1993，13（3）：215-224.LI Tibei，WU Mei.The direct method for spectral and image restoration in high energy astronomy［J］.Acta Astrophysica Sinica，1993，13（3）：215-224（in Chinese）.

［3］ SHEPP L A，VARDI Y.Maximum likelihood restoration for emission tomography［J］.IEEE Transactions on Medical Imaging，1982，1（2）：113-122.

［4］ MU Z P，LIU Y H.Aperture collimation correction and maximum-likelihood image reconstruction for near-field coded aperture imaging of single photon emission computerized tomography［J］.IEEE Transactions on Medical Imaging，2006，25（6）：701-711.

［5］ 何佳偉，劉東升，桂志國.可變有序子集PML 算法在PET 中的應用［J］.中北大學學報：自然科學版，2010，31（6）：646-650.HE Jiawei，LIU Dongsheng，GUI Zhiguo.Application of modified subsets PML algorithm to PET image reconstruction［J］.Journal of North University of China：Natural Science Edition，2010，31（6）：646-650（in Chinese）.