基于在線支持向量機的Mean Shift彩色圖像跟蹤

郭敬明，何 昕，魏仲慧

（1.中國科學院 長春光學精密機械與物理研究所，吉林 長春，130033；2.中國科學院大學，北京100049）

1 引 言

目標跟蹤廣泛應用于智能視頻監控、智能機器人及國防安全方面等領域。如何在視頻序列中對目標進行穩健、實時跟蹤，是計算機視覺領域的熱點問題。穩健性要求算法能夠克服光照、姿態變化，目標快速運動，部分遮擋等干擾因素的影響；實時性要求算法必須有較高的搜索效率，計算耗時少，其實質是如何在當前幀內快速運算鎖定目標。

文獻［1］將目標跟蹤算法分為兩類：一類是基于“濾波、數據關聯”的跟蹤方法，代表為粒子濾波［2］（particle filter）及其改進算法［3－5］；一類是基于“目標建模、定位”的跟蹤方法，代表為Mean Shift［6］及其改進算法［7－8］。由于粒子濾波收斂速度慢，算法復雜度與粒子數成正比，且過多依賴參數，而Mean Shift是一種基于核密度估計的無參數的、基于微分方法的模式匹配搜索算法，計算復雜度低，具有很好的實時性，因此在目標實時跟蹤系統中應用越來越廣泛［9－15］。

盡管Mean Shift應用十分廣泛，但有兩個基本的缺陷：（1）目標模板只能從單一圖像建立；（2）模板很難自適應更新。針對以上問題，相關學者提出了多種改進方案。文獻［5］提出用Mean Shift與粒子濾波相結合的多模式融合跟蹤算法，分別跟蹤后，采用加權參考函數定位目標，但粒子濾波器的復雜計算降低了系統的實時性。文獻［12］提出在線特征選擇機制來對特征進行排序，選擇區分能力最強的特征來建立模板，將顏色R、G、B特征以不同權值組合找到具有更具判決能力的特征，這樣也將大大增加算法的復雜度。文獻［11］研究了跟蹤過程中在線學習的重要性，模型的更新能夠捕獲目標或背景的變化。文獻［10］提出了模板在線更新的Mean Shift算法，通過將跟蹤問題看作目標和背景的分類問題，引入支持向量機（Support Vector Machine）分類函數置信度，將最小化距離函數轉換為最大化分類函數置信度，但其沒有給出在線支持向量機的實現方法，且針對彩色RGB空間加權求得灰度建立目標及背景模型，在光照發生變化或有陰影時有明顯缺陷［15］。

針對上述算法的優缺點，本文提出了基于HSV 彩色空間的在線SVM 的Mean Shift跟蹤算法。為克服RGB 顏色空間在光照變化及陰影效應下的缺陷，將RGB 空間變換到HSV 空間，首先分別建立H、S、V 核直方圖，然后建立統一的HSV 核直方圖，并賦予各分量不同權重，最后將HSV 核直方圖融合到基于在線SVM［13］的Mean Shift跟蹤算法框架中，在計算復雜度不變的情況下，提高了跟蹤定位精度。實驗表明，本文算法優于傳統Mean Shift算法、Particle Filter及文獻［10］算法，穩健性、實時性均有較大提高。

2 Mean Shift跟蹤與支持向量機

2.1 Mean Shift跟蹤

文獻［1］提出了基于核估計的目標跟蹤方法，文中核基的跟蹤方法即為Mean Shift跟蹤方法。目標和候選目標的模型是對圖像目標區域的歸一化核基直方圖向量：

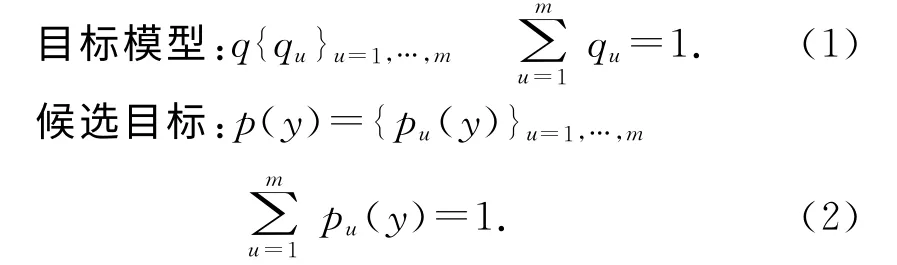
假定目標區域由n個像素點構成｛Xi｝，i＝1，…n構成，其中Xi＝（xi，yi）為圖像像素坐標，直方圖bin量化個數為m，則目標的核直方圖模型為：

式中，δ為Kronecker delta函數。窗口的帶寬矩陣為h，用來限定目標的像素個數。b（Xi）為映射函數，將Xi對應的特征映射到bin值。c為窗口中心位置坐標。k（x）為輪廓函數，為每個像素賦予不同的權值，權值大小與距離目標中心的距離成反比，一定程度上增加了模型的可靠性，因為靠近外側的像素易被遮擋或受背景干擾；同時，使目標函數成為光滑函數，可以由微分法計算。常用的核函數包括高斯核函數和Epanechnikov函數。C 為歸一化系數。

相應地，中心位置位于y 的候選目標模型定義為：

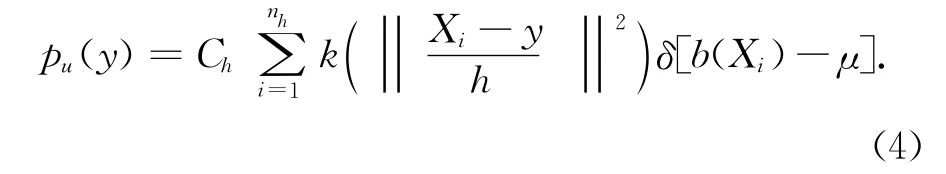
相似性度量函數用來計算在特征空間中目標與候選目標之間的距離。Mean Shift常用的是Bhattacharyya距離：

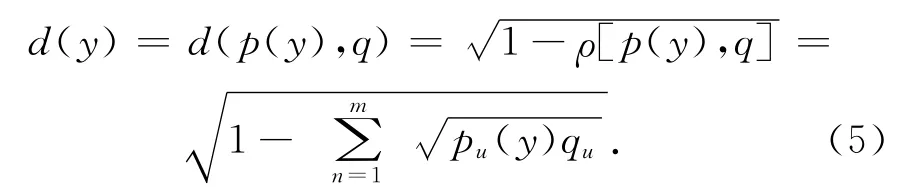
Mean Shift跟蹤原理是找到位置y，使其在所屬特征空間中與目標距離最小，即Bhattacharyya系數ρ［p（y），q］最大。上述優化問題，可以通過以下迭代過程求解：

式中，g（x）＝－k′（x），當｜＾y－y｜＜ε時本幀迭代終止，ε為設定的閾值。

2.2 支持向量機

支持向量機（SVM）是基于VC 維理論和結構風險最小化原理，克服了傳統機器學習中的維數災難問題。SVM 在處理線性不可分問題中應用十分廣泛，通過將訓練數據從輸入空間映射到高維，甚至無限維空間，SVM 求解最優超平面等價于求解如下方程：

求解上式，可以得到SVM 的判別函數：

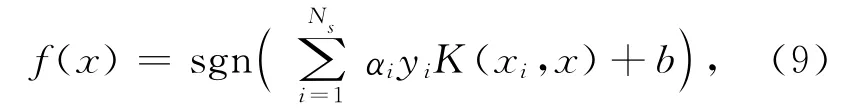
其中：K（xi，x）＝〈Φ（xi），Φ（x）〉，滿足Mercer條件的核函數，常用的核函數有RBF 核函數，多項式核函數等。xi為支持向量，Ns為支持向量個數，αi為 不 同 支 持 向 量 的 權 值，b 為 偏 置 系 數，yi為＋1或－1。

2.3 基于SVM 的Mean Shift跟蹤算法

支持向量機中核函數通常采用RBF核函數、多項式核函數等，但這些函數不是根據概率密度分布來定義的。而Mean Shift是根據顏色直方圖的密度函數進行估計。通過p（xi）建立訓練樣本xi概率密度模型，將核函數作為不同概率分布之間的相似性度量函數，從而建立基于SVM 的Mean Shift跟蹤方法。

式（10）為PPK（probability product kernel）核函數，而傳統Mean Shift 中采用的Bhattacharyya度量函數為ρ＝1／2時的特殊情況。

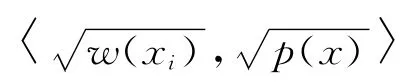
f（x）＞0，代表目標；f（x）＜0，代表背景。q（xi）為第i個支持向量，｜f（x）｜代表置信度，當｜f（x）｜遞增時，表示迭代由初始值向跟蹤目標優化。為了后續與傳統Mean Shift進行對比，這里核函數選擇Bhattacharyya系數，即ρ＝1／2。

將式（11）代入到式（12）中，得到基于圖像窗口的直方圖估計，即候選目標位置的判別函數：

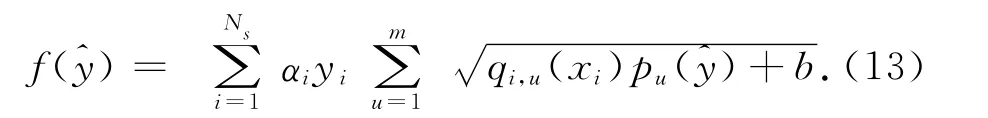
我們對式（13）進行泰勒展開，保留一階量，忽略了二階及高階展開量，得到式（14）：

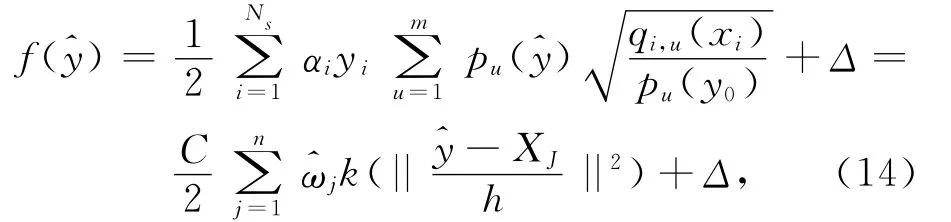
其中：

上述優化問題轉換為使f（＾y）最大，得到迭代求解過程：

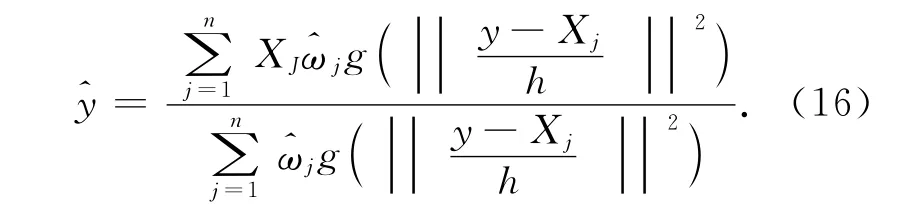
3 基于HSV 空間的在線SVM 的Mean Shift跟蹤算法

傳統Mean Shift方法目標模型由單一圖像建立，且很難更新，當光照、姿態變化，目標快速運動等因素造成模型變化時，極易造成目標跟蹤失敗。為了更新模型，模型必須盡可能多地選擇樣本進行訓練學習。我們把目標跟蹤問題視為目標和背景的分類問題，可以將在線SVM 分類器融合到傳統Mean Shift框架中，使得跟蹤器更加魯棒。當光照條件發生劇烈變化或存在陰影時，R、G、B顏色空間有明顯的缺陷。基于以上分析，提出了基于HSV空間的在線SVM 的Mean Shift彩色圖像跟蹤方法。

3.1 HSV 空間核直方圖

HSV 是人們用來從調色板或顏色輪中挑選顏色所用的彩色系統之一，代表色調、飽和度和亮度值，它比RGB 空間更接近于人們對彩色的感知，在表征陰影及劇烈光照變化方面有更好的效果，可以由RGB轉換得到。

因此，我們將RGB 空間直方圖轉換為HSV空間直方圖作為相似性度量的特征。色調H 取值范圍為0°～360°，紅色為0°，綠色為120°，藍色為240°；飽和度S 取值范圍為0～100%；亮度值V 取值范圍為0～100%。

首先，獲取彩色圖像RGB 值，將RGB 值從0～255歸一化到0～1之間，然后按如下公式將RGB值轉換為HSV 值，為了便于計算，將HSV值轉換到0～255之間：

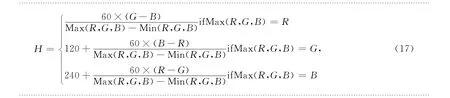
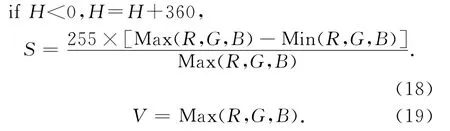
這樣，獲取目標圖像RGB 值后，將RGB 值轉換到HSV 值，得到目標模型HSV 核直方圖分量｛qH，qS，qV｝：

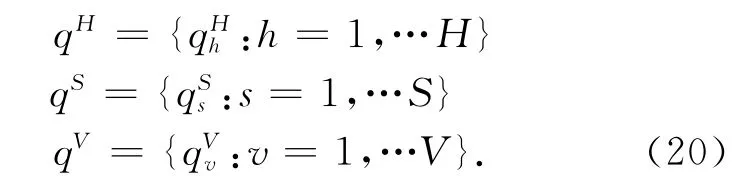
式（20）中，H，S，V 分別為色調、飽和度、亮度直方圖對應的bin值個數；h，s，v 分別為色調、飽和度、亮度對應的bin值。同理，獲取候選目標模型HSV 核直方圖分量｛pH，pS，pV｝。

然后，根據式（5）計算HSV 各分量Bhattacharyya系數：

從而，建立加權合成的統一相似性度量函數。

式（22）中，0≤γ，λ≤1，為預先設定的HSV各分量的權重。依式（22）構造新的滿足核函數性質［14］的核函數為：

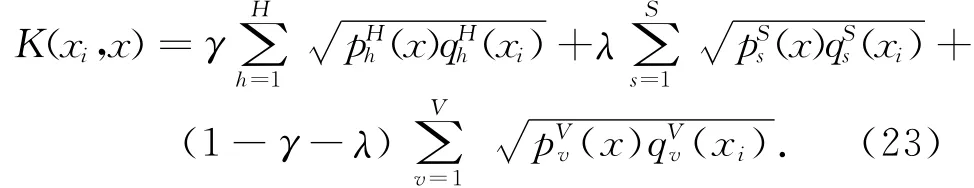
3.2 目標位置確定

根據式（13）及式（23），得到基于SVM 的Mean Shift彩色圖像跟蹤算法判別函數：

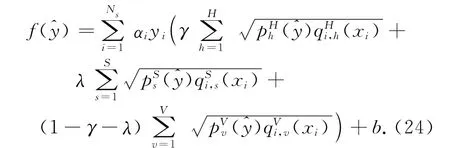
依照（14），通過泰勒展開得到其求解過程：

其中：b1（x），b2（x），b3（x）分別為色調、飽和度及亮度的映射函數。式（26）中，分子部分可以離線計算，因此，其算法復雜度與傳統Mean Shift相同，沒有增加額外的時間消耗。迭代求解式同式（16）。

3.3 模板在線學習

（1）創建初始樣本空間。初始時，在第1 幀圖像中手動選取待跟蹤目標，窗口大小為m×n。按傳統Mean Shift跟蹤式（6）跟蹤N 幀圖像，并依次記錄下每次迭代的中心位置xi（i＝1…N）。將以xi為中心m×n大小的區域圖像按式（17～19）轉換到HSV 空間，依（20）分別計算，得到N個正樣本，即（Xi＝qH（xi）∪qs（xi）∪qV（xi），Yi＝＋1）；同理，可以從這N 幀圖像中任意選取2×N 個m×n大小的不含目標的區域，按上述步驟得到2×N 個負樣本為（Xi′＝qH（xi′）∪qs（xi）∪qV（xi′），Yi′＝－1）。

（2）訓練生成初始支持向量。選取閾值ε及懲罰因子C，核函數為式（23），依據上述N 個正樣本和2×N 個負樣本，訓練計算出（ω0，b0）、分類函數f0及支持向量SV0＝qH（xi）∪qS（xi）∪qV（xi），yi）i＝1…Ns）。

（3）在線支持向量機學習。當跟蹤第N ＋t（t＝1）幀圖像時，依據式（16），（26）迭代求解目標位置，迭代時初始位置選為上一幀目標位置xN＋1。以xN＋1為中心m×n大小區域圖像產生1個新的正樣本，同時，任意選取2 個不含目標的區域產生負樣本，構成新增樣本集It。根據決策函數f0尋找It中 違 反KKT 條 件［13］的 樣 本，記為，違反KKT 判決條件如式（27）所示：

若Ivt為空集，則令SVt＋1＝SVt，ft＋1＝ft，t＝t＋1，轉（3）。否則得到新樣本集T＝SVt∪Ivt，進行重新學習得到SVt＋1，ft＋1，t＝t＋1，轉（3）。

4 算法流程

整個算法的實現過程簡單描述如下：首先手動選取第1幀待跟蹤目標，采用Mean Shift跟蹤第2～N 幀目標，得到當前目標位置的候選值，從每幀生成HSV 空間1 個正樣本和2 個負樣本；然后選擇閾值及懲罰因子等參數，生成初始支持向量和分類函數；最后，跟蹤后續幀時提取新增樣本，根據KKT 條件，判斷是否更新參考模板。算法流程如圖1所示。

圖1 算法流程圖Fig.1 Flow chart of algorithm

5 實驗結果與分析

本文提出的跟蹤算法采用VC＋＋6.0實現，結果仿真采用Matlab7.1 平臺實現。實驗均在Pentium Dual E2180 2.0Hz的PC 平臺上進行。為了驗證本文算法的有效性，對國際通用的兩組CAVIAR 彩色圖像序列［16］進行跟蹤測試，給出了試驗結果。

5.1 HSV 與RGB 直方圖彩色圖像跟蹤對比試驗

第一組為oneleaveshop序列，圖像分辨率為384×288，標 準PAL 制，幀 頻25 f／s，采 用MPEG2壓縮格式。部分跟蹤結果如圖1所示。

圖2中，綠色矩形是傳統Mean Shift跟蹤結果圖，矩形中十字為目標中心；紅色矩形為本文算法跟蹤結果圖。第1幀由手動方式確定待跟蹤的目標，紅、綠兩矩形重合。第28 幀時，傳統Mean Shift算法還能定位準確。但當目標尺寸及姿態發生一定變化時，由于模板的單一性及無法更新，導致目標跟蹤失敗，如第94幀，第175幀。

圖2 oneleaveshop序列跟蹤結果Fig.2 Tracking result on oneleaveshop sequence

圖3給出了初始幀手動選取的目標模板的R、G、B直方圖和H、S、V 直方圖，圖4給出了第175幀中兩種算法跟蹤結果窗口的R、G、B 直方圖和H、S、V 直方圖。可以看出，當目標姿態發生變化時，基于RGB顏色空間的傳統Mean Shift跟蹤器有明顯的缺陷，雖然第1幀與第175幀跟蹤窗RGB 顏色直方圖分布Bhattacharyya系數較大，而目標幾乎完全丟失，導致跟蹤失敗。而HSV 顏色空間在整個彩色序列跟蹤過程中具有良好的抗干擾能力。

圖3 初始幀目標模板直方圖Fig.3 RGB and HSV histogram of target model in frame No.1

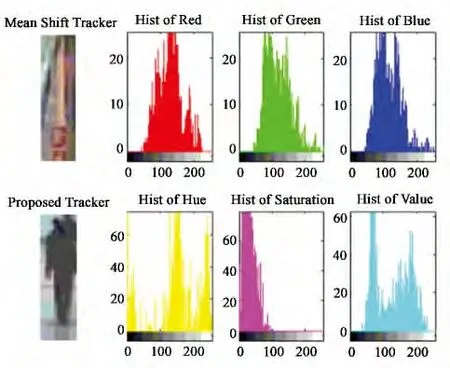
圖4 第175幀兩種算法跟蹤窗口直方圖Fig.4 Histogram of track window by two trackers in frame No.175

5.2 4種跟蹤算法跟蹤性能對比試驗

圖5為Enter Exit序列跟蹤效果圖，圖像分辨率及幀頻同oneleaveshop 序列，與其相比，整個序列中目標姿態及光照都發生了更加劇烈的變化，除了傳統Mean Shift，還增加了粒子濾波和文獻［10］算法進行對比跟蹤實驗，主要考察算法的跟蹤精度及耗時兩個方面。

圖中紅色矩形代表本文算法，藍色矩形代表文獻［10］算法，綠色矩形代表粒子濾波算法（“＋”字代表跟蹤的粒子），青色代表傳統Mean Shift算法。同樣，第1 幀由手動方式確定，4 個跟蹤窗重合。第40 幀時，光照及目標姿態發生微小變化，Mean Shift跟蹤定位誤差最大，導致后續跟蹤失敗。第40幀，第89幀時，粒子濾波還能表現出良好的跟蹤能力，定位誤差較Mean Shift小。但當第157幀時，目標姿態由正面轉為側面，背景及光照也發生較大變化，粒子濾波跟蹤失敗。可以看出，由于背景的變化及目標姿態變化，待跟蹤目標模型發生巨大變化，因此，模型更新是有效跟蹤的必要手段。文獻［10］及本文算法均采用從多幀圖像建立模型及模型自適應更新算法，因此，在整個圖像跟蹤序列中都能夠精確跟蹤目標，尤其在第232幀以后。

圖5 4種跟蹤算法對EnterExit序列跟蹤結果Fig.5 Tracking result on EnterExit sequence by four trackers

圖6，圖7 分別給出了x，y 方向定位偏差。Proposed Tracker代表本文算法；Tracker in［10］代表文獻［10］算法；Standard Mean Shift代表傳統Mean Shift算法；Particle Filter代表粒子濾波算法。

圖6 x 方向偏差Fig.6 Deviation of axis

定位偏差計算公式［7］如式（28）所示：

式中：（xi，yi）為各種算法計算所得目標矩形中心位置，（xc，yc）為通過人工逐幀獲取的目標中心位置。Errori的平方即為圖6、圖7 對應曲線各點的平方和。

表1給出了4種跟蹤算法根據式（28）計算的整個圖像序列定位誤差的均值和方差，單位為像素。FR0.5［10］代表跟蹤窗中心偏離實際目標中心大于0.5像素的幀數占序列總幀數的比例，FR1代表閾值為1 像素時的跟蹤失敗比例。粒子濾波跟蹤器采用100個粒子，調整參數，取10次跟蹤的平均值。可以看出，本文算法跟蹤精度最高，跟蹤失敗率最低。

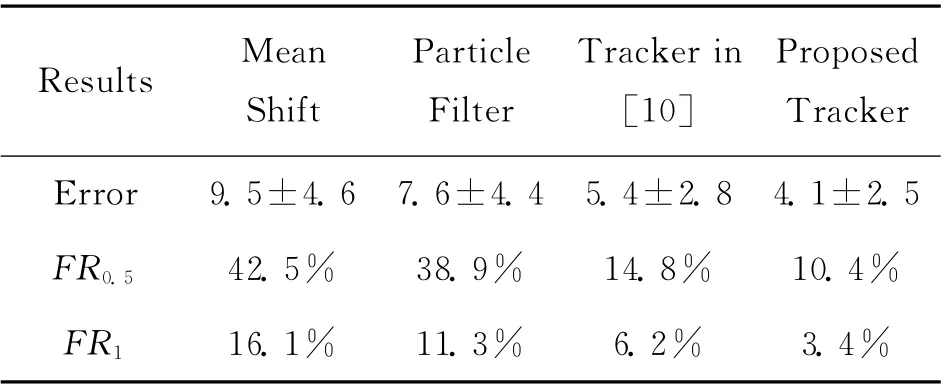
表1 4種跟蹤算法對EnterExit序列跟蹤誤差結果Tab.1 Tracking error of four trackers against the ground truth on EnterExit sequence

表2給出了各自的平均處理時間。粒子濾波收斂速度最慢，消耗時間最長。而本文算法和文獻［10］雖然增加了在線學習，但部分計算因子可以離線進行，其計算復雜度與Mean Shift相當，與支持向量數無關。本文算法對分辨率為384×288的視頻序列，最快處理速度能達到40 f／s。

表2 4種跟蹤算法對EnterExit序列平均處理時間Tab.2 Average computing time of four trackers on EnterExit sequence

6 結 論

針對傳統Mean Shift算法模板從單一圖像建立，且很難更新問題，提出了基于HSV 空間的在線SVM 的Mean Shift跟蹤算法，將RGB顏色空間轉換到HSV 空間，建立新的統一核函數模型，引入增量學習支持向量機算法，對違反KKT條件的樣本進行學習，減少計算量，實現目標模型的在線更新。實驗表明：本文算法對目標姿態、光照及背景發生較大變化時，跟蹤有效且耗時少。當像素大小為384pixel×288pixel（目標尺寸為20pixel×80pixel）時，最快處理速度達40f／s，且跟蹤精度（FR0.5）比傳統Mean Shift提高了32.1%，平均定位誤差為4.1pixel，基本滿足了某些穩健實時跟蹤系統的要求。

［1］ Comaniciu D，Ramesh V.Kernel－based object tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，24（5）：564－577.

［2］ ISARD M，BLAKE A.Condensation－conditional density propagation for visual tracking［J］.International Journal of Computer Vision，1998，29（1）：5－28.

［3］ 杜超，劉偉寧，劉戀.一種基于卡爾曼濾波及粒子濾波的目標跟蹤算法［J］.液晶與顯示，2011，26（3）：384－389.Du C，Liu W N，Liu L.Target tracking algorithm based on Kalman filter and particle filter［J］.Chinese Journal of Liquid Crystals and Displays，2011，26（3）：384－389.（in Chinese）

［4］ 王國良，劉金國.基于粒子濾波的多自由度運動目標跟蹤［J］.光學 精密工程，2011，19（4）：864－869.Wang G L，Liu J G.Moving object tracking with multi－degree－of－freedom based on particle filters［J］.Optics and Precision Engineering，2011，19（4）：864－869.（in Chinese）

［5］ 陳愛華，孟勃，朱明，等.多模式融合的目標跟蹤算法［J］.光學 精密工程，2009，17（1）：185－190.Chen A H，Meng B，Zhu M，et al.Multi－pattern fusion algorithm for target tracking［J］.Optics and Precision Engineering，2009，17（1）：185－190.（in Chinese）

［6］ Comaniciu D，Meer P.Mean shift：A Robust application toward feature space analysis［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24（5）：603－619.

［7］ 王田，劉偉寧，韓廣良，等.基于改進Mean Shift的目標跟蹤算法［J］.液晶與顯示，2012，27（3）：396－400.Wang T，Liu W N，Han G L，et al.Target tracking algorithm based on improved Meanshift［J］.Chinese Journal of Liquid Crystals and Displays，2012，27（3）：396－400.（in Chinese）

［8］ 劉揚，張云峰，董月芳.復雜背景下抗遮擋的運動目標跟蹤算法［J］.液晶與顯示，2010，25（6）：890－895.Liu Y，Zhang Y F，Dong Y F.Anti－occlusion algorithm of tracking moving object in clutter background［J］.Chinese Journal of Liquid Crystals and Displays，2010，25（6）：890－895.（in Chinese）

［9］ Jung U C，SEUNG H J，XU.FPGA－based real－time visual tracking system using adaptive color histograms［C］／／Proceedings of the 2007th International Conference on Robotics and Biomimetics，Sanya，P.R.China：ICRB，2007：172－177.

［10］ Sheng S H，Kim J，Wang H Z.Generalized kernel－based visual tracking［J］.IEEE Transactions on Circuits and Systems for Video Thechnology，2010，20（1）：119－130.

［11］ AVIDAN S.Ensemble tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29（2）：261－271.

［12］ Collins R T，Liu Y X，Leordeanu M.Online selection of discriminative tracking features［C］／／IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（10）：1631－1643.

［13］ Syend N A，Liu H，Sung K.Incremental learning with support vector machines［C］／／Proceedings of the Workshop on Support Vector Machines at the International Joint Conference on Artificial Intelligence，Stockholm，Sweden：IJCAI，1999：2165－2176.

［14］ 李國正，王猛，曾華軍.支持向量機導論［M］.北京：電子工業出版社，2004.Li G Z，Wang M，Zeng H J.An Introduction to Support Vector Machines and Other Kernel－based Learning Methods［M］.Beijing：Publishing House of Electronics Industry，2004.（in Chinese）

［15］ Perez P，Hue C，Vermaak J，et al.Color－Based Probabilistic tracking.［C］∥Lecture Notes in Computer Science，Copenhagan，Denmark：Eccv，2002：661－675.

［16］ The school of Information，University of Edinburgh.CAVIAR Test case Scenarios［DB／OL］.［2011－05－12］／／http：groups.inf.ed.ac.uk／vision／CAVIAR／CAVIARDATA1／.