海雜波中廣義符號恒虛警檢測算法性能分析

劉衛華

（海軍航空工程學院科研部，山東煙臺264001）

在復雜的噪聲背景下保持恒定的虛警概率是設計目標檢測算法必須考慮的問題[1]。當雜波包絡分布類型已知時，通過采集數據來估計某些參數，從而對信號進行有效的檢測，這種檢測方法被稱為參量檢測方法。然而，如果實際雜波分布和假設差距較大，檢測性能就會大幅下降。因此，設計虛警概率與背景分布無關的檢測算法很有必要，這種檢測算法被稱為非參量檢測算法。在背景分布已知的情況下，非參量檢測算法的性能往往不如參量檢測算法，但是在背景分布未知的情況下，非參量檢測算法的性能往往好于參量檢測算法[2]。在雷達實際工作環境當中，雜波分布類型往往無法準確預知，因而非參量檢測方法受到越來越廣泛的關注[3-5]。常見的非參量檢測算法有符號檢測算法[6]，Wilcoxon檢測算法[7]，廣義符號（GS）檢測算 法[2]和Mann-Whitney 檢測算法[8]。GS 檢測算法處理的是經包絡檢波器輸出的回波信號，將檢測單元與周圍參考單元進行比較，并得到相應的非參量化檢驗統計量[7]，是易實現的兩樣本非參量檢測算法之一。

為了研究GS檢測算法對不同類型目標的檢測性能，本文在仿真雜波數據、實測海雜波環境中，對GSCFAR檢測算法的檢測性能和海雜波抑制能力進行了仿真分析。由于GS檢測算法的性能與脈沖數和參考單元數有關[2]，因而本文還研究了脈沖數和參考單元數對GS檢測算法性能的影響。

1 算法模型

1.1 GS檢測算法原理

GS 檢測算法是對接收信號進行多脈沖檢測的兩樣本符號檢測算法。該算法將檢測單元的幅度值與周圍參考單元的幅度值進行比較，得到檢測單元的檢驗統計量，再將檢驗統計量與對應的檢測閾值比較。圖1 給出了GS 檢測算法的原理框圖[7]，檢測單元采樣用yj(j=1,2,…,N) ，參考單元采樣xji(i=1,2,…,M) 。檢測單元兩側各有一個保護單元，防止檢測單元中可能的目標信號泄漏到鄰近的參考單元中而影響檢測。

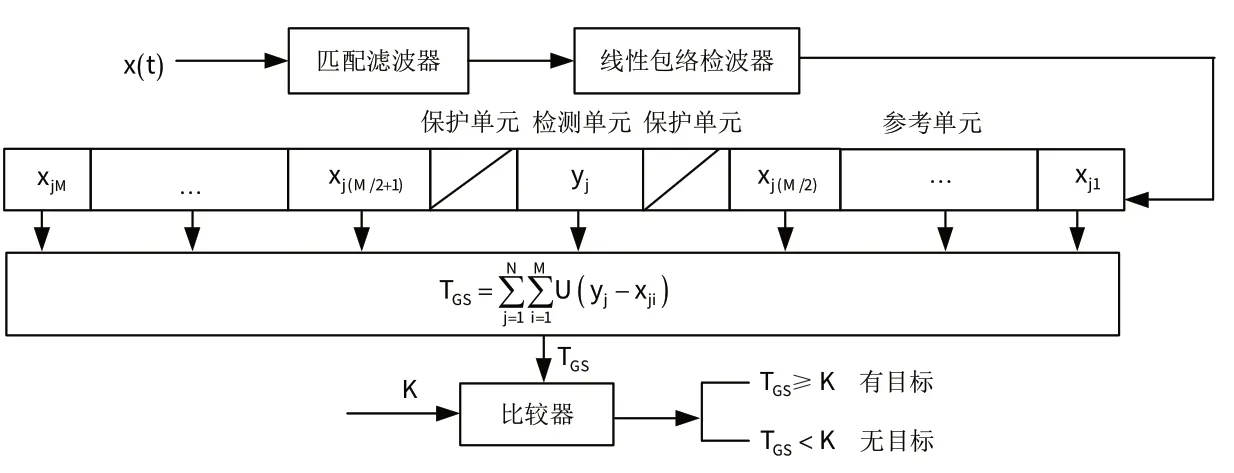
圖1 GS檢測算法原理框圖Fig.1 Schematic diagram of GS detection algorithm

檢驗統計量

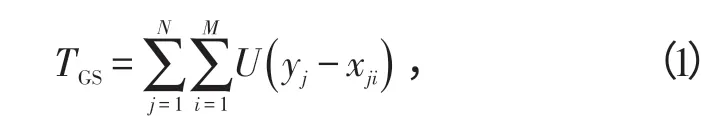
式中：U(?)是單位階躍函數；N為脈沖數；M為參考單元數。

將檢驗統計量TGS和檢測閾值K進行比較，如果TGS≥K，則判決存在目標；如果TGS＜K，則判決不存在目標。在無目標條件下，假設yj滿足獨立同分布；在有目標條件下，假設yj和xji滿足獨立同分布[2]。

1.2 檢測閾值K 的確定

虛警概率Pfa可根據脈沖數N、參考單元數M和檢測閾值K的大小來設定[2]，因而Pfa的值可以N、M和K進行函數表示，具體關系如式（2）所示：

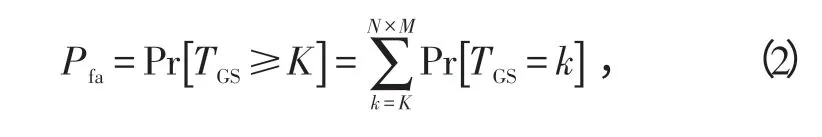
式中，

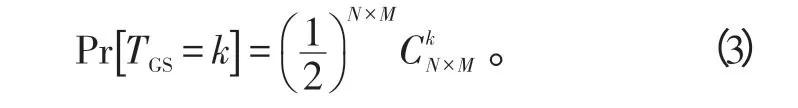
從式（2）可以看出，Pfa不依賴于雜波和噪聲的分布形式，只與K、N和M有關，因而GS檢測算法可使虛警概率保持恒定[7]。

當Pfa、N和M已知時，K可以由Pfa反解出來，那么K也不依賴于雜波和噪聲的分布形式。當Pfa=10-4、N=10、M=16 時，根據上述公式得出K=127。

2 GS檢測算法性能分析

2.1 仿真雜波+目標回波條件下的性能分析

本節采用高斯分布來模擬產生海雜波。分別產生I、Q2路標準高斯分布（均值為0，方差為1）序列，求包絡后作為背景雜波數據。

產生不起伏Swerling 0 型目標回波和快起伏Swerling II型目標回波，將其與雜波數據合成，并調整信雜比（SCR）。

信雜比的計算公式為

當SCR已知時，可以根據上式反推出目標信號的幅度，從而計算出在不同信雜比情況下的檢測概率[9]。

圖2 給出了Pfa=10-3，脈沖數和參考單元數分別改變時，2種目標模型條件下，SCR與檢測概率關系曲線。

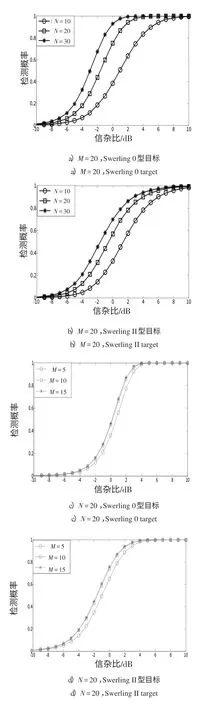
圖2 基于仿真數據的檢測概率與信雜比關系曲線Fig.2 Relationship curve of detection probability and SNR based on simulated data

由圖2可以看出：

1）當脈沖數和參考單元數一定，信雜比在一定范圍內變化時，檢測概率隨著信雜比的增大而不斷增大；

2）在信雜比和參考單元數一定的條件下，隨著脈沖數的增大，檢測概率有所增大；

3）在信雜比和脈沖數一定的條件下，隨著參考單元數的增加，檢測概率有所增大；

4）脈沖數變化對檢測Swerling 0 型目標和Swerling II 型目標的影響要強于參考單元數對檢測2 種目標的影響；

5）在低信雜比條件下，GS檢測算法對Swerling II型目標的檢測性能優于對Swerling 0型目標的檢測性能；在高信雜比條件下，對Swerling 0型目標的檢測性能優于對Swerling II型目標的檢測性能。

2.2 真實雜波+仿真目標回波條件下的性能分析

為進一步驗證不同參數對GS檢測算法性能的影響情況，本節基于某實測數據對GS 檢測算法性能進行分析，實際海雜波背景較為復雜，且分布類型一般是未知的。設Pfa=10-3，雜波數據是通過雷達采集得到的，目標類型仍采用Swerling 0 型和Swerling II 型。圖3給出N和M分別變化時，2種目標模型的SCR與檢測概率的對應關系曲線。

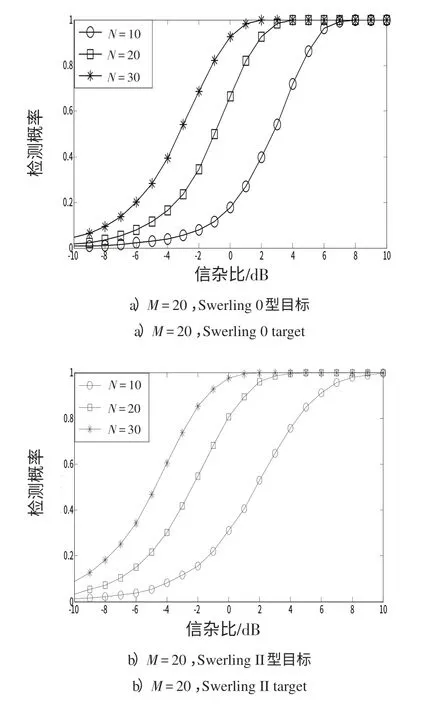
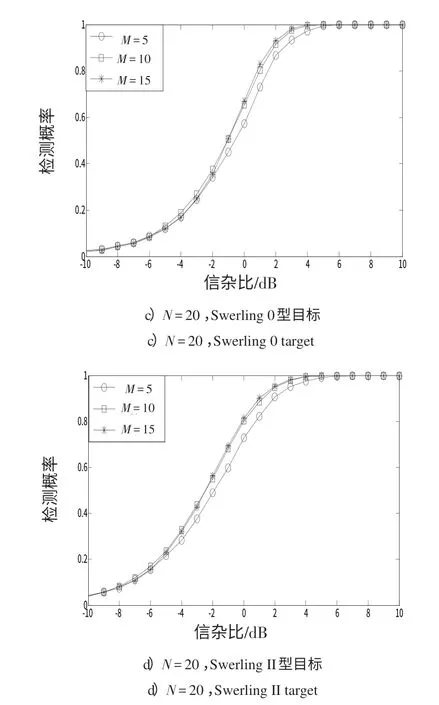
圖3 基于實測數據的檢測概率與信雜比關系曲線Fig.3 Relationship curve of detection probability and SNR based on real data

由圖3可以看出：

1）在其他條件相同的情況下，檢測概率隨脈沖數的增大而有所增大。對于實測數據，在高信雜比條件下，對Swerling 0型目標的檢測能力優于對Swerling II型目標的檢測能力；在低信雜比條件下，對Swerling II型目標的檢測能力優于對Swerling 0型目標的檢測能力；

2）在其他條件相同的情況下，檢測概率隨著參考單元數的增大而有所增大，但變化不明顯；

3）脈沖數變化對檢測Swerling 0 型目標和Swerling II 型目標的影響要強于參考單元數對檢測Swerling 0型目標和Swerling II型目標的影響。

上述分析進一步說明，GS 檢測算法是一種與雜波分布類型無關的檢測方法，即在不同的雜波分布類型情況下，幾種參數對非參量檢測算法性能的影響趨勢保持一致。

分析原因：

1）Swerling II 型目標為快起伏目標，脈沖和脈沖間的起伏是統計獨立的，若前一個脈沖沒有超過門限，則相繼脈沖有可能超過門限；而不起伏目標的相關性較強，如果第一個脈沖振幅小于檢測門限，則相繼脈沖也不會超過門限。在低信雜比條件下，信號幅度較低，快起伏目標經過檢測算法處理之后得到的檢驗統計量超過檢測閾值的概率相對較大而更容易被檢測到；在高信雜比條件下，信號幅度相對較大，相對穩定的不起伏目標經過檢測算法處理之后得到的檢驗統計量要高于快起伏目標，從而更容易被檢測到；

2）GS 檢測算法將檢測單元和周圍的參考單元進行比較以得到檢驗統計量，其本質是對目標優勢的積累。若增大脈沖數，則在脈沖間相對穩定的有用信號的優勢可得到進一步的積累，檢測效果會明顯改善。

2.3 真實雜波+真實目標回波條件下的性能分析

本節基于雷達對海上目標檢測的實測數據進行分析，以驗證GS 檢測算法對漁船目標的檢測性能。圖4給出了虛警概率Pfa=10-3、脈沖數N和參考單元數M分別變化時的二維平面圖。圖4 中縱坐標表示距離單元，橫坐標表示重復掃描的次數，每一個像素點表示一次掃描的回波強度[10]，圖4 a）為原始數據平面圖，圖4 b）~d）為GS檢測算法處理后的顯示結果。

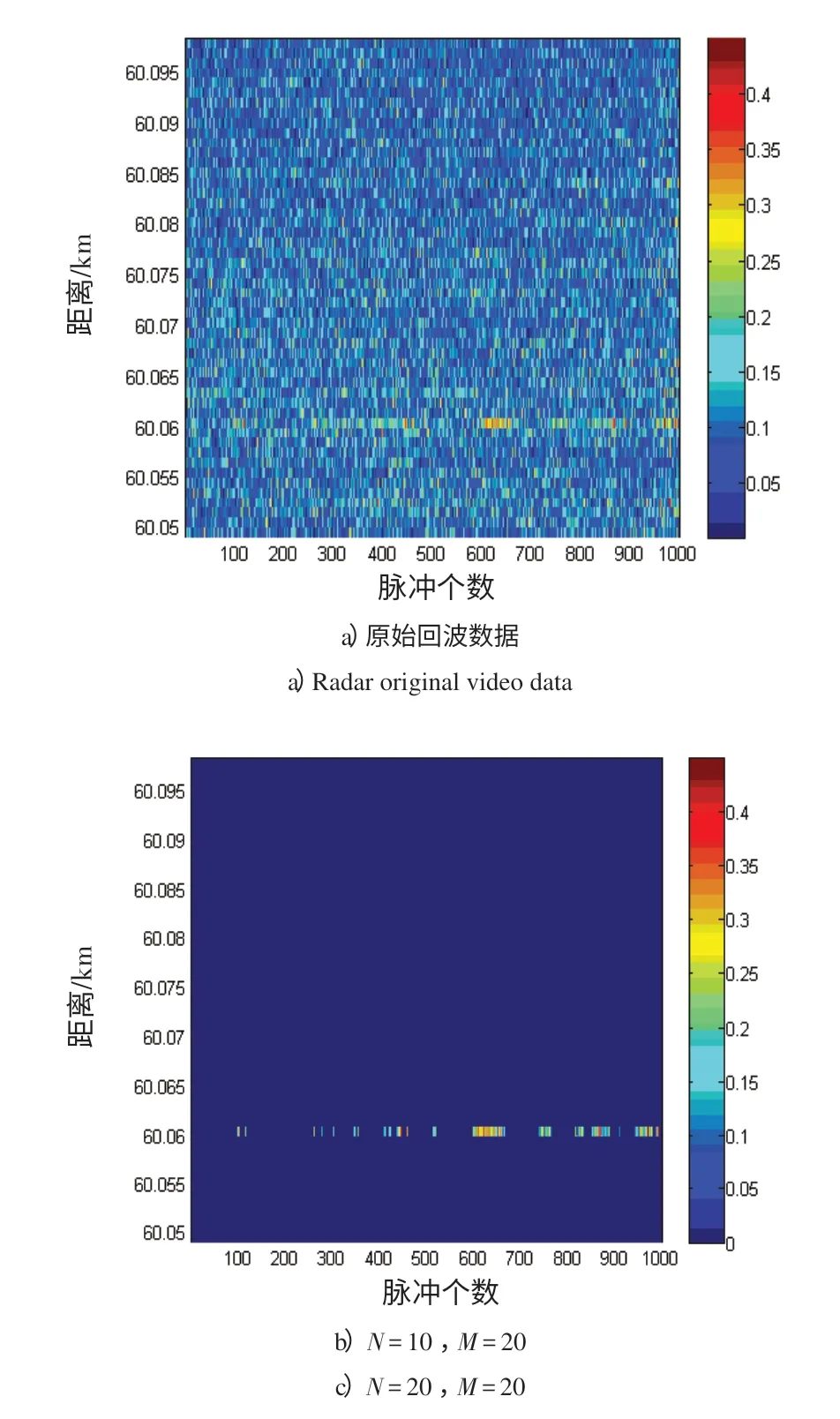
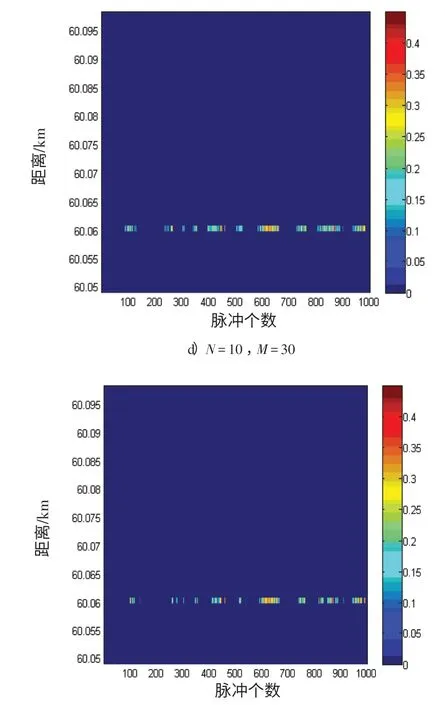
圖4 實測數據顯示圖和檢測算法處理結果Fig.4 Radar original video data and the result of detection algorithm

由圖4 a）可知，在60 km處有1個漁船目標湮沒在海雜波當中，較難分辨；經過GS檢測檢測算法處理后的結果如圖4 b）~d）所示，絕大部分雜波被抑制掉，畫面非常清晰。從圖4可以看出：

1）相比于原始數據平面圖，GS 檢測算法成功檢測出了目標，該檢測算法對雜波有很好的抑制作用。當N增大時，顏色不一的間斷條狀回波逐漸變為連續的條狀回波；

2）對于1 000 次觀測，當M為20，N為10 時，檢測到目標259 次；當M為20，N為20 時，檢測到目標422次；當M為30，N為10時，檢測到目標272次。由此可知，隨著脈沖數N的增多檢測效果明顯變好，但參考單元數M對檢測效果的影響并不明顯。

3 總結

本文利用Swerling 0 和Swerling II 型目標回波疊加仿真雜波和實測海雜波數據，研究了不同參數，即信雜比、參考單元數和脈沖數對GS 檢測算法性能的影響，并采用真實海雜波+目標回波數據進行驗證。結果表明：

1）在高斯雜波背景和實測海雜波背景下，隨著脈沖數、參考單元數和信雜比的增大檢測概率不斷增大，但脈沖數對檢測概率的影響強于參考單元數對檢測概率的影響；在高信雜比條件下，對Swerling 0型目標的檢測能力優于對Swerling II 型目標的檢測能力；在低信雜比條件下，對Swerling II 型目標的檢測能力優于對Swerling 0型目標的檢測能力。

2）通過對實測數據驗證表明，GS 檢測算法可以檢測到海雜波中的漁船，在虛警概率保持不變的條件下，隨著脈沖數和參考單元數的增大，算法的檢測性能得到改善，但是參考單元數對檢測性能的影響并不明顯。

[1] 馬克·理查滋.雷達信號處理基礎[M].3 版.北京：電子工業出版社，2008：260-286.

MARK A RICHARDS. Fundamentals of radar signal processing[M]. 3rd ed. Beijing：Publishing House of Electronics Industry，2008：260-286.（in Chinese）

[2] VILHELM GREGERS HENSEN.Nonparametic radar extraction using a generalized sign test[J]. IEEE Transactions on Aerospace & Electronic Systems，1971，7（5）：941-950.

[3] SEYEF B，SHARAFAT A R. Signed-rank nonparametric multiuser detection in non-gaussian channels[J]. IEEE Transactions on Information Theory，2005，51（4）：1478-1486.

[4] HAO CHEN. Noise enhanced nonpatametric detection[J].IEEE Transactions on Information Theory，2009，55（2）：499-506.

[5] ORTON M.Nonparametric rank detectors under k-distributed clutter in radar application[J]. IEEE Transactions on Aerospace&Electronic Systems，2005，41（2）：702-710.

[6] CARLYLE J W. On nonparametric siganl detectors[J].IEEE Transactions on Information Theory，1964，10（2）：146-152.

[7] 何友，關鍵. 雷達目標檢測與恒虛警處理[M]. 2 版. 北京：清華大學出版社，2011：230-250.

HE YOU，GUAN JIAN. Radar target detection and cfar processing[M]. 2rd ed. Beijing：Tsinghua University Press，2011：230-250.（in Chinese）

[8] ZEORI G W. Performance of a two-sample mann-whitney nonparametric detector in a radar application[J].IEEE Transactions on Aerospace & Electronic Systems，1971，7（5）：951-959.

[9] 趙志堅.海雜波中非參量恒虛警檢測算法性能分析[J].雷達科學與技術，2010，8（1）：65-73.

ZHAO ZHIJIAN. Performance analysis of nonparametric CFAR detectors in sea clutter[J].Radar Science and Technology，2010，8（1）：65-73.（in Chinese）

[10] 張林. 三種兩樣本非參量檢測器CFAR 檢測算法分析[J].海軍航空工程學院學報，2011，26（3）：296-300.

ZHANG LIN.Performance analysis of three kinds of twosample nonparametric CFAR detectors[J]. Journal of Navel Aeronautical and Astronautical University，2011，26（3）：296-300.（in Chinese）