模糊環(huán)境下的投資決策期望值模型

□文/董朝霞 崔占豪 徐佳鑫 王曉

（河北金融學(xué)院河北·保定）

一、背景介紹

投資決策問題是指投資者為了實(shí)現(xiàn)自己的預(yù)期投資目標(biāo)，運(yùn)用一定的科學(xué)理論、邏輯方法及技術(shù)手段，通過一定的程序?qū)ν顿Y的必要性、投資目標(biāo)、投資規(guī)模、投資方向、投資結(jié)構(gòu)、投資成本與收益等經(jīng)濟(jì)活動中重大問題所進(jìn)行的分析、判斷和方案選擇。眾所周知，現(xiàn)代的投資決策問題具有一定的風(fēng)險性，從而要求投資者應(yīng)及時考慮到實(shí)際投資決策過程中將出現(xiàn)的各種可測或不可測的變化。為了對投資決策中的風(fēng)險做出合理準(zhǔn)確的估計，眾多學(xué)者根據(jù)以往的歷史資料并通過科學(xué)的方法進(jìn)行風(fēng)險控制研究工作，從而可以有效降低投資決策中的風(fēng)險，并獲得最大化的投資利潤。范龍振和唐國興假定投資項(xiàng)目的價值和初始投資支出是隨時間變化的幾何布朗運(yùn)動，利用期權(quán)定價的理論和方法，給出了投資時間選擇權(quán)帶來的投資機(jī)會的價值和相應(yīng)的投資決策方法，并討論了投資的時間選擇權(quán)對投資決策的影響。韓其恒等提出了一類概率準(zhǔn)則下的兩期投資決策問題，并對證券收益率為連續(xù)及離散型隨機(jī)變量這兩種情況分別進(jìn)行了討論。

隨著美國控制論專家Zadeh（1965）提出的模糊集理論的不斷發(fā)展，模糊模型及相應(yīng)算法得到了迅速發(fā)展。袁國強(qiáng)（2009）提出了一類兩階段模糊生產(chǎn)計劃期望值模型及混合智能算法。袁國強(qiáng)等（2009）提出了一類新的模糊生產(chǎn)計劃期望值模型，并通過模型性質(zhì)轉(zhuǎn)化為經(jīng)典的線性規(guī)劃模型。袁國強(qiáng)（2009）提出了一類新的帶有模糊參數(shù)的生產(chǎn)計劃模型并設(shè)計了相應(yīng)的混合智能算法。因此，本文首先將基于可信性理論提出一類新的投資決策期望值模型；然后，通過模型的基本性質(zhì)將模糊投資決策期望值模型轉(zhuǎn)化為經(jīng)典的線性規(guī)劃模型；最后，本文給出一個具體的證券投資決策問題的例子來表明所設(shè)計模型的實(shí)用性。

二、模糊投資決策期望值模型

在本文的以下討論中，假設(shè)采用下面的指標(biāo)和參數(shù)：

i=1，2，…，n：投資有價證券的數(shù)量；

Ai：第i種有價證券；

ai：第i種有價證券的信用等級；

bi：第i種有價證券的到期年限；

ci：第i種有價證券的到期稅前收益率；

xi：投資第i種有價證券的金額；

k：在n種有價證券中選出固定投資的m種有價證券至少所需投資的金額總數(shù)；

K：投資者現(xiàn)有的投資金額總數(shù)；

a：投資者可以接受的所購證券的平均信用等級；

b：投資者可以接受的最高所購證券的平均到期年限。

使用上面的記號，為了得到帶有模糊參數(shù)的投資決策期望值模型，本文首先建立以下帶有確定參數(shù)的投資決策模型：

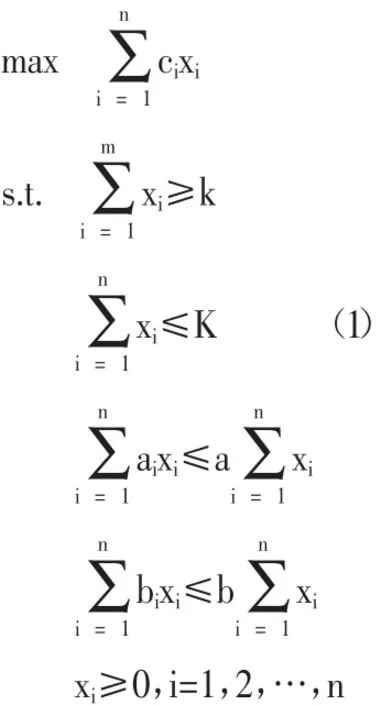
由于現(xiàn)實(shí)的投資決策中存在大量的風(fēng)險因素，例如銀行利率、信用風(fēng)險、交易風(fēng)險、操作風(fēng)險和市場風(fēng)險等。投資者通過有限的信息要想得到最大的投資利潤就必須合理地對各種投資風(fēng)險進(jìn)行妥善處理。由于有價證券的稅前收益率受到以上各種因素的影響，從而本文將到期稅前收益率看作連續(xù)型三角模糊變量，即模糊稅前收益率ci（γ）i=1，2，…，n，這里假設(shè)各個模糊變量是相互獨(dú)立的。因此，通過以上引入的模糊參數(shù)可以建立下面模糊環(huán)境下的投資決策期望值模型：

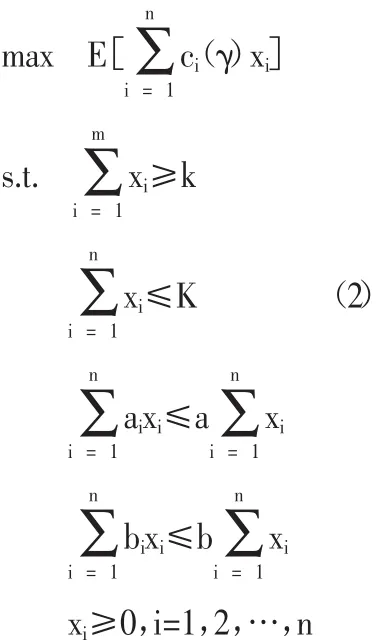
由于以上模糊投資決策期望值模型（2）中的模糊變量是相互獨(dú)立的，所以根據(jù)Liu和Liu（2002）中的相關(guān)理論可以將模型（2）轉(zhuǎn)化為下面的經(jīng)典線性規(guī)劃：

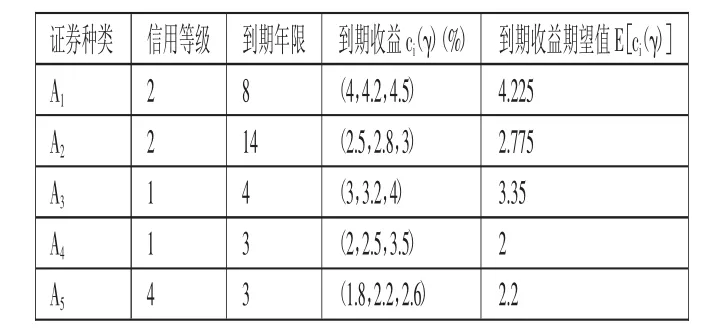
表1 證券投資決策問題相關(guān)數(shù)據(jù)

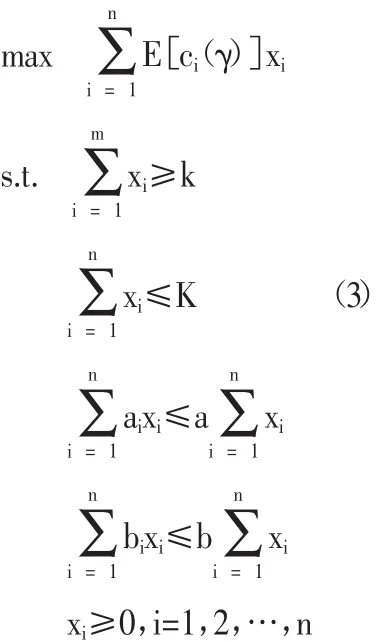
這里，由于模型（3）是一個經(jīng)典的線性規(guī)劃問題，從而可以采用經(jīng)典的線性規(guī)劃問題算法進(jìn)行求解。

三、模糊證券投資決策問題實(shí)例

下面給出一個證券投資決策的例子來說明上述模糊投資決策模型的實(shí)用性。假設(shè)某投資者計劃用1，100萬元資金進(jìn)行五種有價證券的投資，并且可供購進(jìn)的證券、信用等級、到期年限、到期稅前收益如表1所示。（表1）基于以上數(shù)據(jù)，建立模糊環(huán)境下的證券投資決策期望值模型：

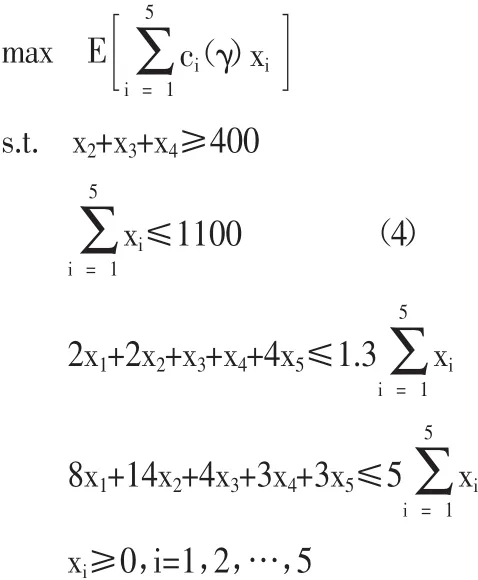
這里，要求第3種、第4種和第5種證券至少要購進(jìn)400萬元；所購證券的平均信用等級不超過1.3；所購證券的平均到期年限不超過5年。由于模型（4）中的模糊變量均假設(shè)是相互獨(dú)立的，所以根據(jù)模型（2）和模型（3）的轉(zhuǎn)化可以得到下面的線性規(guī)劃模型：

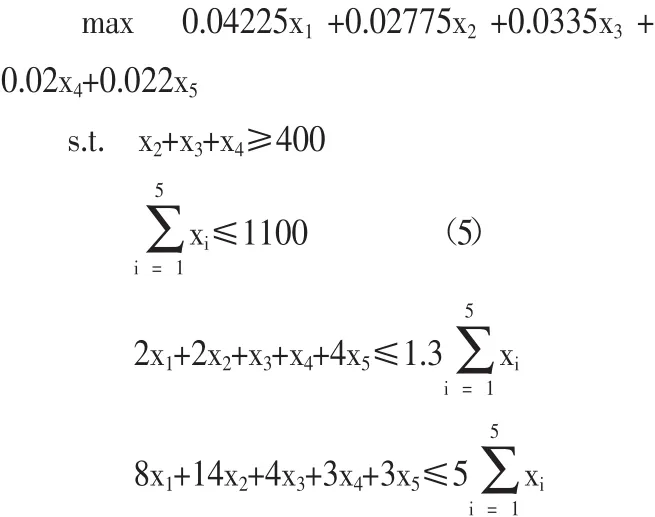
xi≥0，i=1，2，…，5

為了求解模型（5），本文利用三角模糊變量的期望值公式已經(jīng)分別計算出了各個模糊收益率ci（γ）的期望值E［ci（γ）］，見表1。然后，可以利用Lingo軟件求解模型（5）。最后可以得到模型（5）的最大收益值為39.25625萬元，最優(yōu)解為第1種證券投資275萬元；第3種證券投資825萬元。

［1］韓其恒，唐萬生，李光泉.概率準(zhǔn)則下的兩期投資決策問題［J］.管理科學(xué)學(xué)報，2002.2.［2］范龍振，唐國興.投資機(jī)會的價值與投資決策［J］.系統(tǒng)工程，1998.9.

［3］Zadeh L A.Fuzzy sets［J］.Information and control，1965.8.

［4］袁國強(qiáng).兩階段模糊生產(chǎn)計劃期望值模型［J］.應(yīng)用數(shù)學(xué)學(xué)報，2009.6.

［5］袁國強(qiáng)等.基于可信性理論的生產(chǎn)計劃期望值模型［J］.數(shù)學(xué)的實(shí)踐與認(rèn)識，2009.5.

［6］袁國強(qiáng).帶有模糊參數(shù)的農(nóng)業(yè)生產(chǎn)計劃模型［J］.模糊系統(tǒng)與數(shù)學(xué)，2009.8.

［7］Liu B，Liu Y K.Expected value of fuzzy variable and fuzzy expected value models［J］.2002.10.