圓柱尾流中眼鏡蛇探針與熱線的性能對比

王漢封,李卓峰,林祥德

(1.中南大學 土木工程學院,長沙 410075; 2.中南大學 高速鐵路建造技術國家工程實驗室,長沙 410075)

收稿日期: 2013-10-19;修訂日期: 2014-12-11

基金項目: 國家自然科學基金(51108468)

引用格式:WangHF,LiZF,LinXD.Comparisonoftheperformanceofcobraprobeandhotwireincircularcylinderwake.JournalofExperimentsinFluidMechanics,2014,28(5): 104-110.王漢封,李卓峰,林祥德.圓柱尾流中眼鏡蛇探針與熱線的性能對比.實驗流體力學, 2014,28(5): 104-110.

0 引 言

不同類型的多孔探針在三維流場測量中已有了很多成功的應用。由于壓力傳感器頻響和測壓管道阻尼等限制，傳統多孔探針只能用于平均速度的測量[1-3]。近來，隨著微型壓力傳感器的應用，已出現了可測量瞬態速度和壓力的多孔探針[4]。目前，國內外應用較為廣泛的可測量瞬時速度的多孔探針是澳大利亞湍流儀器(TFI)公司的“眼鏡蛇探針(Cobra Probe)”，其外形結構如圖1所示。

(a) 探針尺寸(毫米)

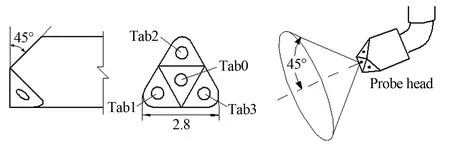
(b) 探針頭部外形 (c) 測量風向角范圍

本研究在二維圓柱尾流中對眼鏡蛇探針與渦量型熱線探針[13-14]的測量結果進行了詳細的對比，包括平均速度、雷諾應力、湍流高階關聯量、概率密度分布、自相關系數以及頻譜特性等，為眼鏡蛇探針在鈍體尾流中的應用提供參考。

1 實驗裝置與參數

1.1眼鏡蛇探針

實驗所用眼鏡蛇探針為TFI公司Series100型，如圖1所示。該探針頭部寬度約2.8mm，呈三角形，每個角上有一45°切面，因其外形類似于眼鏡蛇而得名。探針頭部每個三角形截面中心均有一個直徑為0.5mm的測壓孔，如圖1(b)所示。測壓孔通過內徑為0.5mm的管道與集成在探針尾部桿內的壓阻式電橋型壓力傳感器連接，用來測量每個測壓孔上的瞬態壓力。簡而言之，探針監測頭部4個面上的瞬時壓力，修正測壓管道阻尼作用后，通過標定函數轉換為3個方向的瞬時速度值。實驗中所使用的四孔眼鏡蛇探針，在全部偏航角與傾斜角測量范圍內，標定函數始終包含每個測孔的壓力信息，這有利于提高測量精度和簡化標定函數。傳統七孔探針采用分區標定的方法，其角度測量范圍可達±70°左右[16]。而眼鏡蛇探針空間角度測量范圍明顯小于七孔探針，為一個±45°的圓錐形區域，如圖1(c)所示。眼鏡蛇探針的風速測量范圍由其壓力傳感器量程決定，本實驗所用探針測量范圍為2～50m/s。在湍流強度30％以內，眼鏡蛇探針可精確到±0.5m/s，角度的測量精度為±1°。Series100型眼鏡蛇探針的頻率可達2kHz，理論上能夠分辨出1kHz以下的湍流能譜[7]。

1.2渦量型熱線探針

渦量型熱線探針由4個X熱線探針組成，已有大量文獻對這種探針進行了報道[13-14]，故本文只做簡要介紹。 X探針僅能測量其所在平面內的2個方向上的速度分量。渦量型熱線探針中的4個X熱線A、B、C和D的位置和所測量的速度如表1所示。例如，X熱線B是由3、4號熱絲構成，處在(x,y)平面內，可測量x方向與y方向速度分量u和v。X探針的2根熱絲間距約為0.7mm。渦量探針中相對的2個X探針中心點間距，即圖2中Δy和Δz，均為2.7mm。由此可知，本實驗所用的渦量探針與眼鏡蛇探針頭部的幾何尺寸非常接近，故2者空間分辨率相當。渦量探針中各熱絲為直徑dw=2.5μm的鉑銠合金絲，熱絲的有效長度為200dw左右(約0.5mm)。渦量探針可測量各方向上的速度梯度和3個方向上的瞬態渦量等信息，但本研究僅需要其所測量的u，v和w3個速度分量與眼鏡蛇探針的測量結果進行對比。

表1 渦量型熱線探針所含X熱線的位置及其所測速度分量

圖2 渦量探針

1.3實驗介紹

實驗在直流式風洞內進行，風洞實驗段截面為0.45m×0.45m，長1m。實驗段風速3～42m/s，湍流度小于0.5％。2種探針的測量分別在直徑d=12.7mm的光滑圓柱下游x=10d的位置上進行。x、y和z分別代表流向、側向與展向，對應速度為u，v和w。圓柱貫穿風洞試驗段，其長徑比約為35，可近似視為二維。實驗中風洞阻塞度為2.8％，其影響可忽略不計。實驗風速為U∞=8.5m/s，對應雷諾數Red=7200。

2 結果與討論

2.1時均統計量

圖3 湍動能與眼鏡蛇探針數據拒絕率

上述2種測試方法所得雷諾應力的差異比管道流或射流中的差異略大[11,12]，這可能是因為本實驗中圓柱直徑較小，因此尾流中平均速度剪切較強且湍流尺度較小。Guo和Wood[12]對比射流中不同流向位置上的測量結果發現，隨著流向距離的增加，眼鏡蛇探針與熱線探針測量結果的差異有所減小，他們推測平均速度剪切以及湍流尺度對Cobra探針測量結果的影響較熱線更為顯著。考慮到本文中圓柱直徑較小，平均速度剪切和湍流尺度的影響將更為顯著，這可能是造成2種方法所得湍流統計量存在較大差異的重要原因。

圖 4 時均流向速度與雷諾應力和

圖5 時均三階關聯量與

2.2概率密度函數特性

常用三階和四階統計量，即偏度S(Skewness)和峰度K(Kurtosis)，來描述隨機信號概率密度函數的對稱性與凸起程度[19,20]。S與K的定義如式(1)所示：

(1)

其中：x為變量u或v；σx為x的均方根值；n為樣本數量。對于高斯分布，偏度S=0，峰度K=0。如圖6所示，在尾流中心|y*|<1的范圍內，Su與Ku均接近于0，可知該范圍內u接近于高斯分布。而在|y*|>1區域內，Su<0而Ku>0，說明u的分布不再對稱且相對于高斯分布其峰值更為集中。值得注意的是，眼鏡蛇探針和熱線探針所測得的Su與Ku在整個尾流中均比較接近。相對而言，2種方法測得的Sv與Kv的差異相對較大，尤其是在|y*|>1的范圍內，差異更為顯著，且眼鏡蛇探針的測量結果在數值上始終大于熱線探針測量結果。除y*=0附近，Sv均不為0，且Kv也始終不為0，這表明整個尾流中v的分布始終被尾流中渦街等擬序結構控制，而不屬于高斯分布。

圖6 速度u和v的偏度與峰度

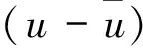
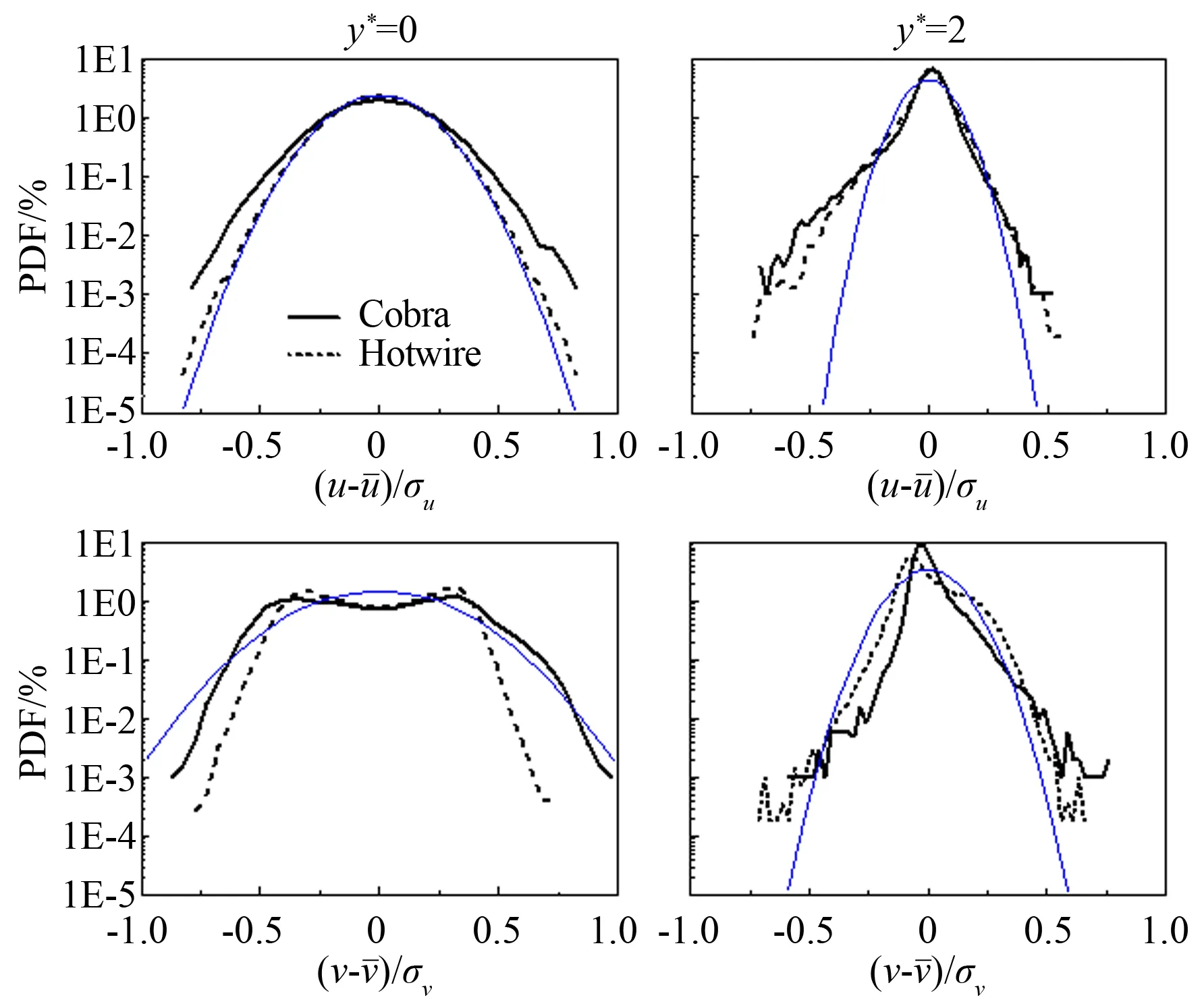
圖7 脈動速度的概率密度分布函數(藍線為標準高斯分布)

圖8給出的是y*=0處眼鏡蛇探針與熱線探針測量得到的瞬態速度方向角的概率密度分布，其中α為(x，y) 平面內u與v的夾角，β為(x，z) 平面內u與w的夾角。2種方法測量得到的β角的概率分布非常相似，且接近均值為0的高斯分布。相對而言，2種方法所得到的u與v夾角α的差異更為顯著。在熱線測量結果中，α在±π/8附近有突出的2個峰值，而在|α|>3π/16范圍內，其概率迅速減小并趨于0。造成α雙峰分布的原因與v的雙峰分布的原因(見圖7)是相同的，即尾流中心會受到圓柱兩側脫落的正負渦團的作用。眼鏡蛇探針測量得到的α角度范圍要明顯大于熱線的對應結果，例如，α=±3π/16時，眼鏡蛇探針所測α的概率仍有4％左右。考慮到兩者u的概率分布較為接近(見圖7) ，α概率分布差異主要應歸因于眼鏡蛇探針測試結果高估了速度v。

圖8 y*=0處速度方向角的概率密度分布函數：α、β分別為為u-v、u-w夾角

2.3相關系數與頻譜特性

眼鏡蛇探針相對于傳統多孔探針的主要優勢之一是其頻響較高，可達到2kHz。正是因為這一特性，眼鏡蛇探針被認為可在一定程度上取代熱線風速儀。且已有文獻將其用于計算湍流能譜或估算湍流積分尺度等[6,7,9]。圖9給出了尾流中心眼鏡蛇探針與熱線所測瞬時速度u和v的自相關函數Ru與Rv。本實驗中熱線采樣頻率為10.4kHz，而眼鏡蛇探針為2kHz，因此前者的時間分辨率遠高于后者。如圖9所示，前者可給出t*=0.01附近的相關系數，而后者僅能給出t*>0.1范圍內的數據。兩者自相關系數Ru存在明顯差異，主要表現在以下2點：(1) 眼鏡蛇探針的相關系數Ru在t*為整數時有突出的峰值，說明其所測u速度相對于熱線具有更顯著的周期性。這可能是因為其時間分辨率較低，造成其測量結果u不能反映隨機性更強的高頻小尺度湍流脈動的影響；(2) 熱線與眼鏡蛇探針所測的Ru首次過零值對應時間分別為t*=7.4和1.3，兩者存在顯著差異。文獻中通常依據Taylor假設和自相關函數Ru估算湍流積分尺度[21]，因此眼鏡蛇探針將明顯低估尾流中的湍流積分尺度。

相對于Ru，速度v的自相關函數Rv表現出了強烈的周期性，這表明尾流中速度v對周期性Karman渦街更為敏感[13]。圖9中用紅色虛線給出了Rv衰減過程的包絡線，可以發現熱線所測Rv的衰減速率要快于眼鏡蛇探針的相應結果。例如，t*=30時(即間隔30個渦脫落周期) 熱線與眼鏡蛇探針的Rv對應值分別為0.12和0.24。這與造成2種方法所測Ru的周期性出現明顯差異的原因是類似的，即眼鏡蛇探針由于無法反應出高頻小尺度隨機脈動的影響，會明顯高估v的相關性。

圖9 尾流中心瞬時速度u與v的自相關函數

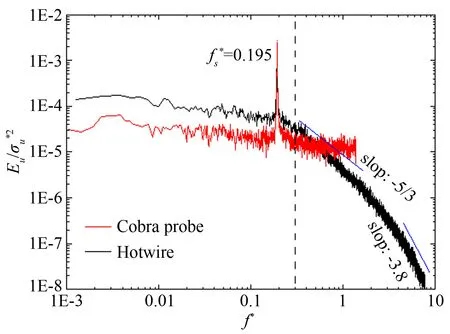
圖10 尾流中心速度u與v的能譜

3 結 論

通過對眼鏡蛇探針與熱線在Red=7200的二維圓柱尾流中的測量結果進行詳細對比，包括時均速度、雷諾應力、湍流高階關聯量、概率密度分布、自相關系數和能譜等，可獲得如下主要結論：

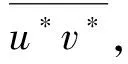
(3) 由于無法反應高頻小尺度脈動的影響，眼鏡蛇探針所測自相關系數Ru和Rv相對于熱線具有更強的周期性。從u和v的能譜可以看出，造成2種測量方法所測雷諾應力存在差異的主要原因是高頻部分的不同。而對于相對較低的渦脫落頻率，2種方法均能獲得較為準確的結果。

(4) 眼鏡蛇探針所測u與v的能譜在慣性子區內存在明顯差異，不能像熱線一樣反映出慣性子區內小尺度湍流的各項同性。即使眼鏡蛇探針的頻響可達2kHz，但仍不適合湍流譜特性(尤其是高頻部分) 的研究。

參考文獻:

[1]Summner D,Heseltine J L,Dansereau O J P.Wake structure of a finite circular cylinder of small aspect ratio[J].Exp.in Fluids,2004,37: 720-730.

[2]王志強,胡駿,羅鉅,等.多級軸流壓氣機靜子通道三維流場測量[J].推進技術,2012,33(3): 371-376.

Wang Zhiqiang,Hu Jun,Luo Ju,et al.Investigation of Three-Dimension Flow in a Multi-Stage Compressor Stator[J].Journal of Propulsion Technology,2012,33(3): 371-376.

[3]李鵬,馬興宇,明曉.多孔探針系統誤差分析[J].實驗流體力學,2012,26(5): 69-73.

Li Peng,Ma Xingyu,Ming Xiao.System error analysis on multi-hole probe[J].Journal of Experiments in Fluid Mechanics,2012,26(5): 69-73.

[4]Shepherd I C.A four-hole pressure probe for fluid flow measurement in three dimensions[J].J Fluids Eng,1981,103: 590-594.

[5]Schneider G M,Hooper J D,Musgrove A R,et al.Velocity and Reynolds stresses in a precession jet flow[J].Exp in Fluids,1997,22: 489-495.

[6]Hemida H,Gil N,Baker C.LES of slipstream of a rotating train[J].J Fluids Eng,2010,132: 051103-2.

[7]Mallipudi S,Selig M,Long K.Use of a four-hole Cobra pressure Probe to determine the unsteady wake characteristics of rotating objects[C]//24thAIAA Aerodynamic Measurement Technology and Ground Testing Conference,Portland,Oregon,28 June-1 July,2004.

[8]韓艷,陳政清.薄平板復氣動導納函數的實驗與數值模擬研究[J].振動工程學報,2009,22(2): 200-206.

Han Yan,Chen Zhengqing.Experimental and numerical simulation studies on complex aerodynamic admittance functions of thin plate section[J].Journal of Vibration Engineering,2009,22(2): 200-206.

[9]McAuliffe B R,Larose G L.Reynolds-number and surface-modeling sensitivities for experimental simulation of flow over complex topography[J].J Wind Eng Ind Aerodyn,2012,104-106: 603-613.

[10]華旭剛,陳政清,楊靖波,等.大縮尺比氣彈模型風洞試驗紊流積分尺度修正[J].建筑結構學報,2010,31(10): 55-61.

Hua Xugang,Chen Zhengqing,Yang Jingbo,et al.Turbulence integral scale corrections to aeroelastic wind tunnel experimental results with large scale model[J].Journal of Building Structures,2010,31(10): 55-61.

[11]Hooper J D,Musgrove A R.Reynolds stress,mean velocity,and dynamic static pressure measurement by a four-hole pressure probe[J].Exp Thermal Fluid Sci,1997,15: 375-383.

[12]Guo Y,Wood D H.Instantaneous velocity and pressure measurements in turbulent mixing layer[J].Exp Thermal Fluid Sci,2001,24: 139-150.

[13]Zhou T,Mohd Razali S F,Zhou Y,et al.Dependence of the wake on inclination of a stationary cylinder[J].Exp Fluids,2009,46: 1125-1138.

[14]Zhou T,Wang H F,Mohd Razali S F,et al.Three dimensional vorticity measurements in the wake of a yawed circular cylinder[J].Phy Fluids,2010,22: 015108.

[15]Chen J,Hanynes B S,Fletcher D F.Cobra probe measurements of mean velocities,Reynolds stresses and high order velocity correlations in pipe flow[J].Exp Thermal Fluid Sci,2000,21: 206-217.

[16]李彥,李衛東.七孔探針三維自動測速系統[J].實驗技術與管理,2006,23(1):42-44.

Li Yan,Li Weidong.3-D Velocity Automatic Measuring System Using 7-holes Pitot Tube[J].Experimental Technology and Management,2006,23(1): 42-44.

[17]Guo Y,Hooper J D,Wood D H.Instantaneous velocity and pressure measurements in a plane turbulent mixing layer[C]//13thAustralasian Fluid Mechanics Conference,Melbourne,Australia,13-18 Dec,1998.

[18]Zhou Y,Zhang H J,Yiu M W.The turbulent wake of two side-by-side circular cylinders[J].J Fluid Mech,2002,458: 303-332.

[19]Giofre M,Gusella V,Grigoriu M.Non-Gaussian wind pressure on prismatic building.II: numerical simulation[J].J Struc Eng,2001,127: 990-995.

[20]林巍,樓文娟,申屠團兵,等.高層建筑脈動風壓的非高斯峰值因子法[J].浙江大學學報(工學版),2012,46(4): 691-697.

Lin Wei,Lou Wenjuan,Shentu Tuanbing,et al.Peak factor of non-Gaussian pressure process on complex super-tall building[J].Journal of Zhejiang University(Engineering Science),2012,46(4): 691-697.

[21]王龍花,王浩,宗周紅,等.蘇通大橋實測強風湍流積分尺度的對比研究[J].空氣動力學學報,2013,31(4):533-540.

Wang Longhua,Wang Hao,Zong Zhouhong,et al.Comparable study on turbulence integral scale of measured strong wind on Sutong Bridge[J].Acta Aerodynamica Sinica,2013,31(4): 533-540.

作者簡介:

王漢封(1976-)，男，河南開封人，副教授，博士。研究方向：實驗流體力學、流動控制。通信地址：中南大學土木工程學院(410075)。E-mail: wanghfme@gmail.com