基于低偏差序列的礦井供水管網可靠性

蔣仲安，王佩，施蕾蕾，譚聰

(北京科技大學 金屬礦山高效開采與安全教育部重點實驗室，北京，100083)

礦井供水管網作為礦山安全避險六大系統之一，其可靠穩定運行是保證綜合防塵效果的重要基礎。一個完善可靠的防塵供水系統能夠維持礦山正常的采掘工作，保證礦工具有安全的工作環境，同時供水管網是防治井下粉塵危害的重要設施，因此對礦井防塵供水管網的可靠性進行研究非常必要。國內對城市供水管網可靠性研究較多，方法也眾多。而礦井供水管網研究較少[1-3]，主要分析方法有故障樹分析法[4]和GO 法[5-6]。針對傳統蒙特卡羅法[7-9]收斂速度較慢以及計算結果不夠穩定的問題[10]，本文作者采用擬蒙特卡羅法對礦井供水管網水力可靠性進行研究。該方法采用Sobol 序列進行抽樣替換了傳統蒙特卡羅法的偽隨機數，加快了收斂速度，提高了仿真結果的穩定性。在對管網進行分析的過程中，將綜合考慮機械故障和水力條件變化對管網可靠性的影響，并運用EPANETH 管網平差軟件進行水力模擬，以模擬結果為基礎值代入水力可靠性分析模型進行計算。EPANET 管網平差軟件是美國環保局開發的一款免費軟件，它可以通過自帶組件繪制管網模型，還包含強大的水質、水力模擬能力，而EPANETH 是其漢化版。

1 擬蒙特卡羅法

擬蒙特卡羅法(OMC)是基于蒙特卡羅法的一種改進方法，采用在采樣空間分布更加均勻的擬隨機數代替傳統蒙特卡羅法中的偽隨機數。擬隨機數一般由低偏差序列通過某種變換得到。擬蒙特卡羅法計算的收斂速度和結果的準確性主要取決于偏差。偏差用來度量點列在函數域上分布的均勻程度，偏差越小，點列分布越均勻，收斂速度就變快，波動也隨之減小，計算準確度就相應地提高[11]。

根據Kokama-Hlawka 定理[12]，低偏差序列M 用于蒙特卡羅積分時具有確定的誤差上界。因此擬蒙特卡羅法的計算誤差可由Kokama-Hlawka 不等式給出：

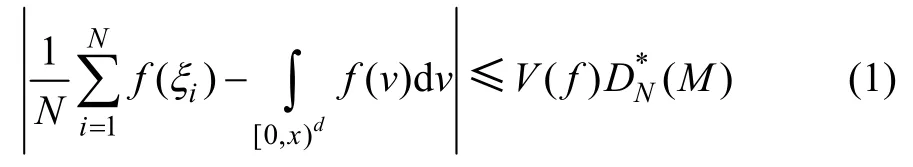
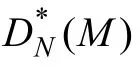
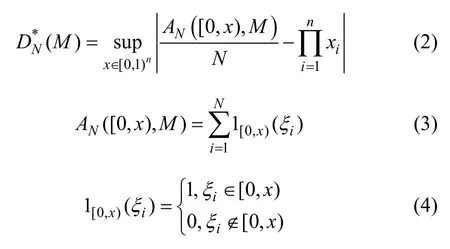
式中：AN([0,x),M)為序列M 中的N 個樣本在區間[0,x)中的數量。

由于Sobol 序列較其他序列收斂效果好，計算精確，本文首次采用Sobol 序列用于礦井防塵供水管網的可靠性計算。Sobol 序列的產生方法如下[15]：

Sobol序列是基于一組叫做“直接數”的數vi而構造的。設mi是小于2i的正奇數，則vi=mi/2i。

vi的生成借助于系數只為0 或1 的本原多項式，多項式可表示為

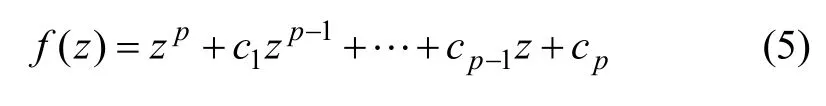
對于i＞p，存在遞歸公式：

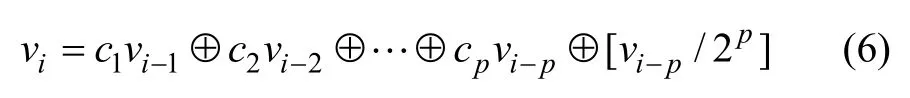
式中：⊕為二進制按位異或運算符。

對于任何一個十進制整數n，可以唯一表示成與數基b=2 有關的式子

式中：k 為大于等于log2n 的最小整數，aj取0 或1。

則Sobol 序列的第n 個元素為：

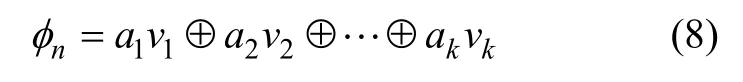
為了加快序列的產生速度，Antonov 和Saleev[16]提出了Gray code 法，可將式(17)修正為：

式中：i 為滿足aj=0 的最小的j。

2 礦井供水管網水力可靠性計算

2.1 供水管網水力可靠性評價模型建立

在分析礦井防塵供水管網水力可靠性時，由于要建立數學模型，因此必須對一些參數進行界定。首先，界定管網組件只有正常與故障2 種狀態，而供水節點有正常、失效以及非正常3 種狀態，并且在所有管網組件中，只考慮管段故障對供水管網可靠性的影響；其次，管網組件的故障率λ 和修復時間T 均為常數，且組件或系統的故障和修復相互獨立。

在分析整個管網可靠度之前，從管網中各節點著手。節點流量與水頭之間的關系可用下式表示[17]：

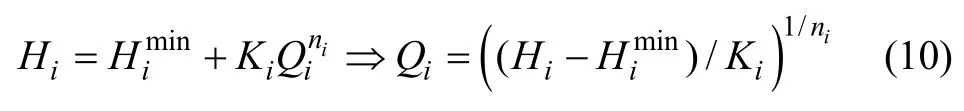
式中：Hi為節點i 的水壓；Himin為節點i 要求的最小水壓；Qi為節點i 的流量；Ki為節點i 的阻力系數；ni為節點i 的阻力指數。

節點需水量和節點所需水壓的關系可表示為：

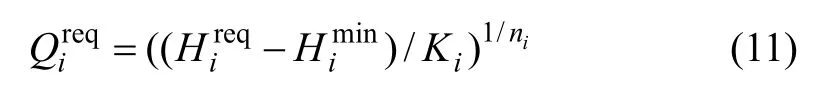
式中： Qireq為節點i 的需水量；Hireq為節點i 所需水壓。

由式(10)和(11)可得：

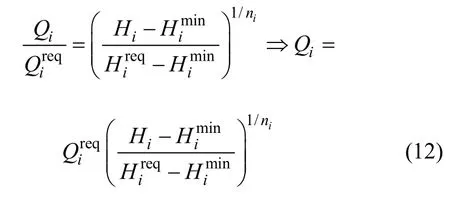
從式(10)可看出：節點流量與節點水壓之間滿足指數關系，因此在挑選評價指標時可只選1 個指標，本文選擇節點水量作為評價指標之一。節點可用水量可用下式表示：

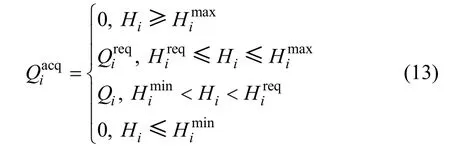
式中，Himax為節點i 能夠承受的最大水壓。

從式(13)可以看出：當節點水壓高于所需水壓且低于允許的最大水壓時，水量滿足要求；當水壓低于所需水壓、高于要求的最小水壓時，水量部分滿足要求；當水壓高于管網能夠承受的最大水壓時，雖然能夠提供充足的水量，但存在隱患，容易導致爆管等事故，此時定義節點失效；當水壓低于要求的最小水壓時，節點失效。

本文節點可靠度用需水量的滿足程度表示，則節點可靠度可表示為：

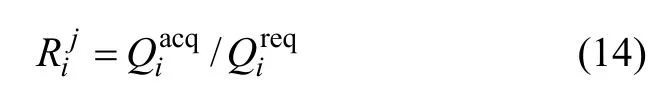
式中， Rij為管網中第j 根管段發生故障時，節點i 的可靠度。

由式(13)和(14)可得：

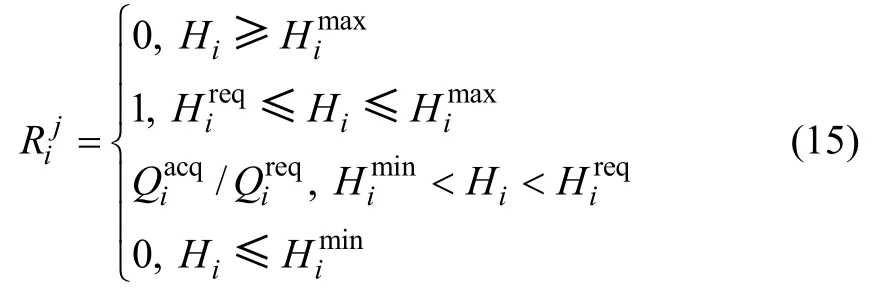
取分析時間為1 a(365 d)，則1 a 中節點的概率可靠度為：

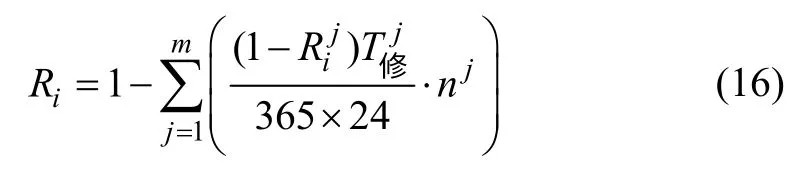
為了體現每個節點對整個供水管網的影響程度，以節點需水量占管網總流量的比例為權值，對整個管網進行綜合評價，建立如下數學模型：

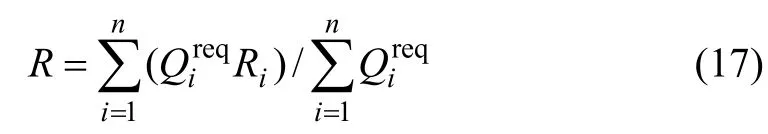
式中：R 為管網水力可靠度；n 為管網節點數；Qireq為節點i 的需水量；Ri為節點i 的概率可靠度。Ri和R分別從局部和整體2 個方面反映了管網的可靠性。

通過以上分析可知：用于研究礦井防塵供水管網的可靠性評價的指標有管段管徑、管長、故障率、修復時間以及節點用水量。

2.2 礦井供水管網可靠性評價模型求解流程

基于擬蒙特卡羅法的礦井供水管網可靠性評價基本步驟為：

(1) 運用EPANETH 管網平差軟件建立供水管網模型，通過假定管網中的每根管段發生故障，求解對應于每根管段故障狀態下的節點可用水量，根據式(15)求得各節點的水力可靠度。

(2) 確定供水管網各管段的故障率λ。統計資料顯示，管網發生故障次數的分布規律近似于泊松分布，

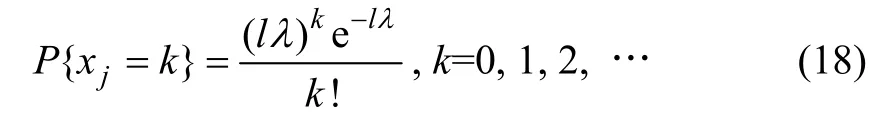
式中：xj為管段j 1 a 內發生故障的次數；l 為管段j的長度，km；λ 為故障率，次/(a·km)。

(3) 產生數量足夠多的Sobol 序列。

(4) 進行抽樣，觀察收斂結果，根據精度要求確定模擬次數，穩定值即為節點的概率可靠度和管網水力可靠度。

(5) 對N 個樣本值進行統計分析，估計均值、標準差和其他統計特征。

3 實例應用

將評價模型用于范各莊礦的供水管網，該管網以-124 m 處靜壓水池為主水源。經過簡化，管網中共有20 個節點，19 根管段。運用EPANETH 建模后的各參數信息見圖1。管段基本信息見表1。

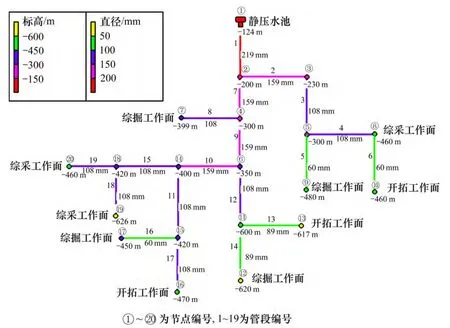
圖1 EPANETH 建立管網模型Fig.1 Network model of EPANETH

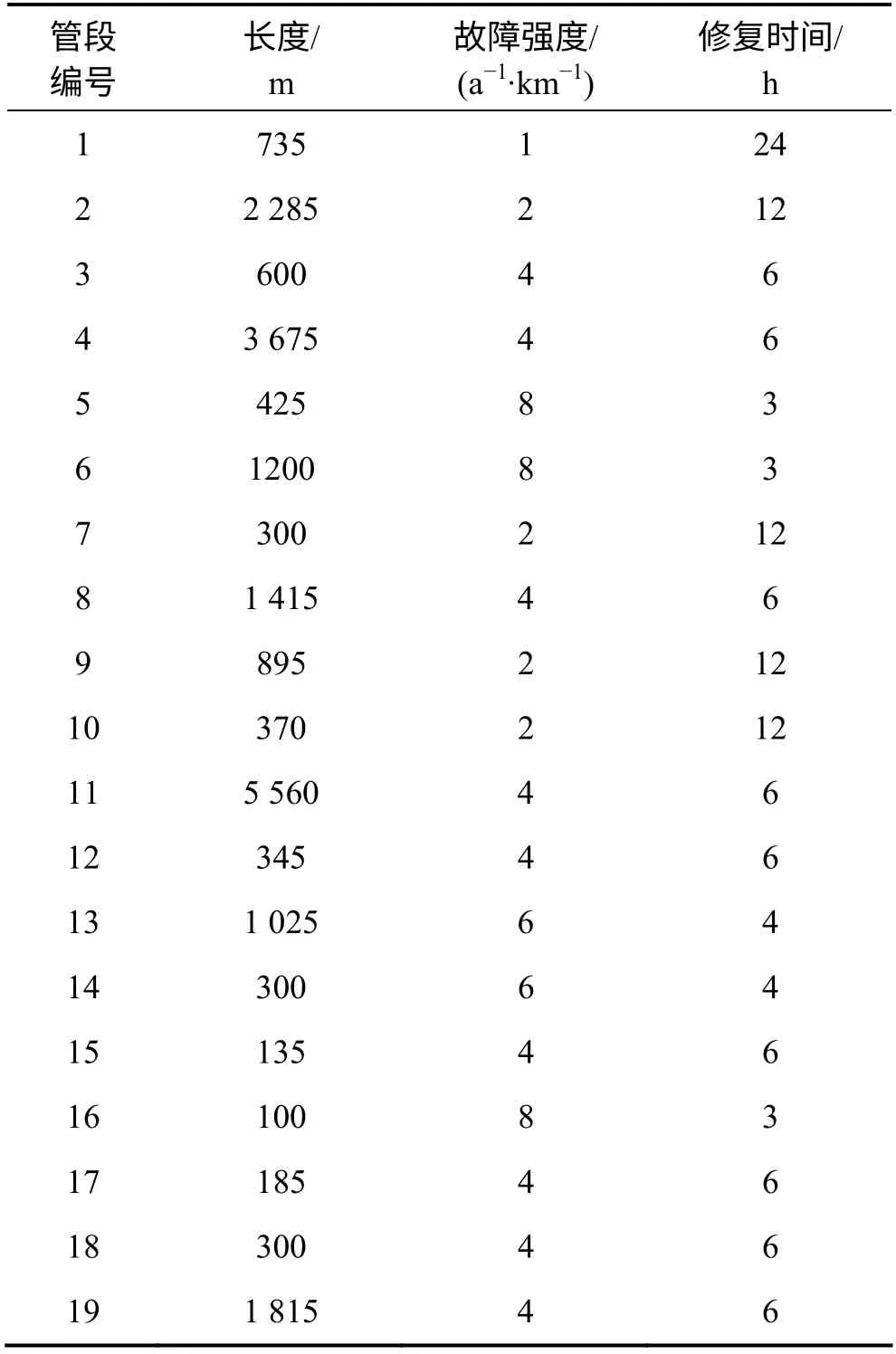
表1 管段基本信息表Table 1 Basic information of pipes

通過EPANETH 對管網中各管段發生故障時的供水情況進行仿真模擬，得到各節點的可用水量，代入式(15)得到對應各管段故障時的節點可靠度。將管網中各節點對應于19 根管段故障狀態下的節點可靠度取平均值，具體結果見表2。將管網中各管段發生故障時對應于所有節點的可靠度取平均值，求得管網瞬時水力可靠度，結果見表3。該值反映了管段對管網可靠度的影響程度，是定位關鍵管段的重要依據。

從表2 可以看出：節點可靠度均值為1 的點為水源節點，其余節點的可靠性都會因為管段發生故障而受到影響。離水源較遠的節點可靠度較低，這是因為遠離水源的節點依賴的管段比靠近水源的節點要多。

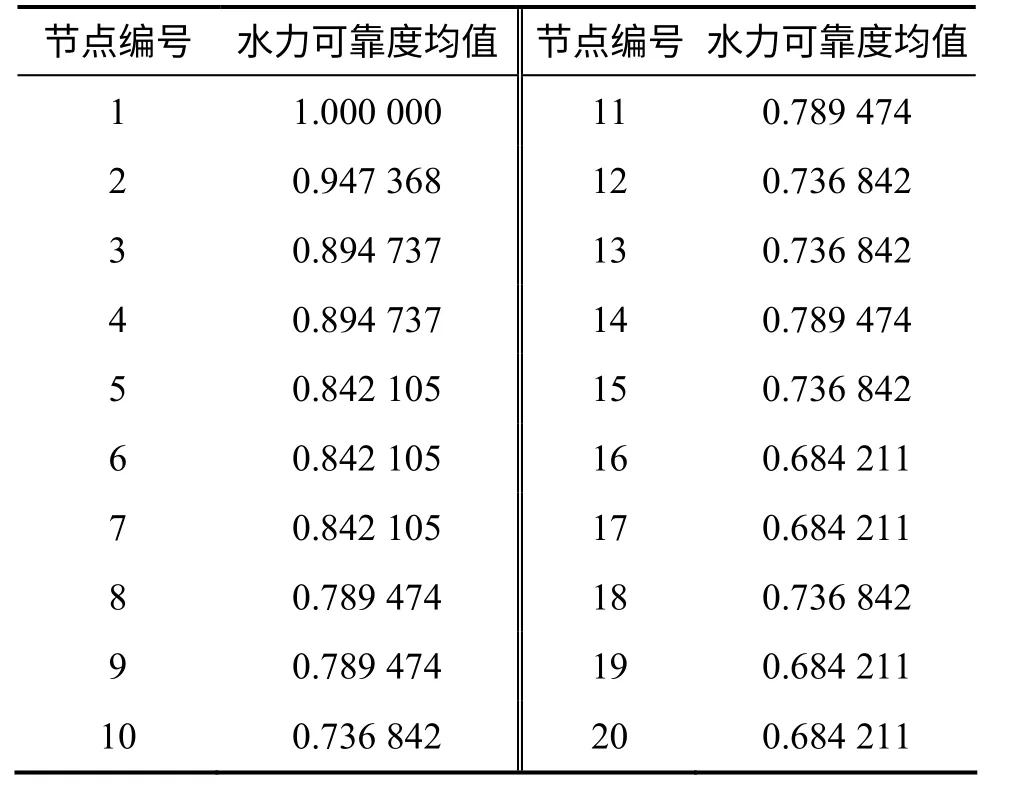
表2 故障時節點水力可靠度均值Table 2 Mean of node hydraulic reliability in trouble

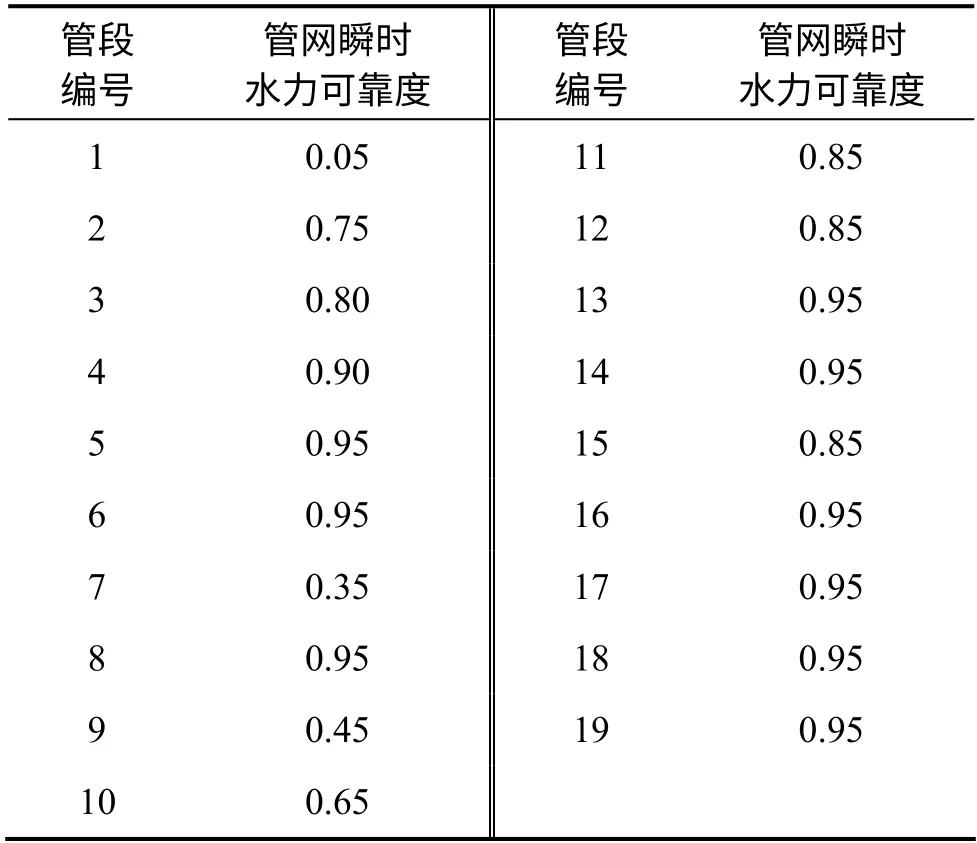
表3 故障時管網瞬時水力可靠度Table 3 Transient hydraulic reliability of network in trouble

從表3 可以看出：管段1 的瞬時可靠度較低，對管網中各節點的可靠性的影響最大，因為該管段為主水源與管網的連接管段，承擔著主要的供水任務。從整體上來看，靠近水源的管段一般對管網的可靠性影響較大，遠離水源的管段對整個管網的可靠性影響較小。與范各莊礦實際礦井供水管網情況相符。

確定節點的可靠度后，采用擬蒙特卡羅法進行抽樣，確定管網中每根管段發生故障的次數，并求得各節點的概率可靠度，再以節點需水量占管網總流量的比例為權值，求得整個管網的可靠度。該過程通過matlab 編程實現。模擬后得到的管網可靠度如圖2 所示，其標準差如圖3 所示。本文取標準差為0.000 2以下時的結果為管網水力可靠度，根據本例的模擬結果，經過997 次模擬后標準差達到0.000 2，此時的管網可靠度為0.979 169。

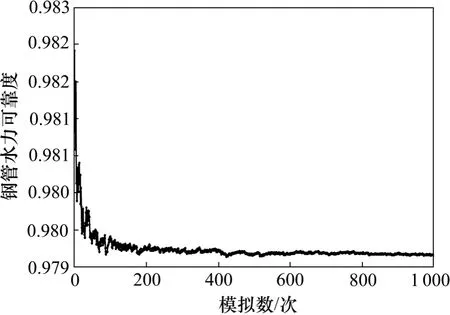
圖2 管網可靠度模擬結果Fig.2 Simulation result of network’s reliability

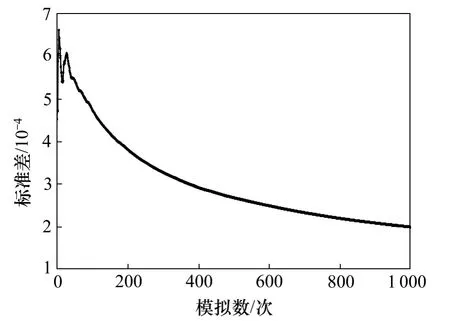
圖3 管網水力可靠度模擬標準差Fig.3 Standard deviation of network’s reliability

4 結論

(1) 采用了Sobol 序列作為擬蒙特卡羅法的核心求解部分，提出了礦井防塵供水管網水利可靠性研究的新方法，并將方法運用于實例，為以后管網優化研究提供了參考。

(2) 提高管網水力可靠性的主要方法有降低管段故障率和減少修復時間即加快維修速度。

(3) 供水管網的拓撲結構對管網水力可靠度有著重要的影響，良好的拓撲結構能使管網系統在某些管段發生故障時，斷水范圍較小，管網的供水能力下降不大。

(4) 對于管網系統中不可修復或難以修復的組件，應該采用可靠性較高的設備，以降低發生故障的可能性。

[1] 張立松, 閆相禎, 楊秀娟, 等. 煤巖破碎失效概率的可靠性分析及分級應用[J]. 煤炭學報, 2012, 37(11): 1823-1828.ZHANG Lisong, YAN Xiangzhen, YANG Xiujuan, et al.Reliability analysis of coal crushing failure probability and its classification application[J]. Journal of China Coal Society, 2012,37(11): 1823-1828.

[2] 肖尊群, 劉寶琛, 喬世范, 等. 重力式擋土墻結構模糊隨機可靠性分析[J]. 中南大學學報(自然科學版), 2010, 41(4):1522-1526.XIAO Zunqun, LIU Baochen, QIAO Shifan, et al. Analysis of fuzzy reliability for gravity retaining wall structure[J]. Journal of Central South University (Science and Technology), 2010, 41(4):1522-1526.

[3] 曾晟, 楊仕教, 孫冰, 等. 基于ABAQUS-ANFIS 的露天礦邊坡可靠度分析[J]. 煤炭學報, 2006, 31(4): 437-441.ZENG Sheng, YANG Shijiao, SUN Bing, et al. Reliability analysis of open-pit slope based on ABAQUS and ANFIS[J].Journal of China Coal Society, 2006, 31(4): 437-441.

[4] 侯曉東, 蔣仲安. 礦井防塵供水管網失效模糊故障樹分析[J].金屬礦山, 2008(6): 112-115.HOU Xiaodong, JIANG Zhongan. Fuzzy fault tree analysis of failure of water supply network for mine dust-proofing[J]. Metal Mine, 2008(6): 112-115.

[5] 金溪, 張杰, 高金良, 等. 利用GO 法進行供水管網可靠度計算[J]. 浙江工業大學學報, 2007, 35(6): 682-685.JIN Xi, ZHANG Jie, GAO Jinliang, et al. Calculation of water supply system reliability with GO method[J]. Journal of Zhejiang University of Technology, 2007, 35(6): 682-685.

[6] 桑海濤, 孟稚松, 周真. 礦井防塵供水管網系統的GO 法可靠性分析[J]. 科學技術與工程, 2010, 10(28): 6989-6993.SANG Haitao, MENG Zhisong, ZHOU Zhen. Reliability analysis of water supply network system for mine dust-proofing in GO methodology[J]. Science Technology and Engineering,2010, 10(28): 6989-6993.

[7] 鄧建, 邊利, 彭懷生. 一種新的蒙特卡羅隨機有限元方法[J].中南大學學報(自然科學版), 2006, 37(5): 998-1000.DENG Jian, BIAN Li, PENG Huaisheng. A new Monte-Carlo stochastic finite element method[J]. Journal of Central South University (Science and Technology), 2006, 37(5): 998-1000.

[8] 章征寶, 余云進, 徐得潛, 等. 基于蒙特卡羅法的城市給水管網可靠性分析[J]. 給水排水, 2007, 33(7): 106-110.ZHANG Zhengbao, YU Yunjin, XU Deqian, et al. The reliability analysis of urban water distribution network based on Monte-Carlo method[J]. Water & Wastewater Engineering, 2007,33(7): 106-110.

[9] 李龍云. 蒙特卡羅法在給水管網可靠性評價中的應用[D]. 上海: 同濟大學環境科學與工程學院, 2009: 13-14.LI Longyun. Application of Monte-Carlo method in reliability evaluation of water distribution network[D]. Shanghai: Tongji University. College of Environment Science and Engineering,2009: 13-14.

[10] 黃美發, 景暉, 匡兵, 等. 基于擬蒙特卡羅方法的測量不確定度評定[J]. 儀器儀表學報, 2009, 30(1): 120-124.HUANG Meifa, JING Hui, KUANG Bing, et al. Measurement uncertainty evaluation based on quasi Monte-Carlo method[J].Chinese Journal of Scientific Instrument, 2009, 30(1): 120-124.

[12] 朱堯辰. 點集偏差引論[M]. 合肥: 中國科學技術大學出版社,2011: 190-193.ZHU Yaochen. Point set deviation introduction[M]. Hefei:University of Science and Technology China Press, 2011:190-193.

[13] 朱云飛, 羅彪, 鄭金華, 等. 基于擬蒙特卡羅方法的進化算法搜索魯棒最優解的性能提高研究[J]. 模式識別與人工智能,2011, 24(2): 201-204.ZHU Yunfei, LUO Biao, ZHENG Jinhua, et al. Research on increasing the performance of evolutionary algorithm in searching robust optimal solutions based on Quasi-Monte Carlo method[J]. Pattern Recognition & Artificial Intelligence, 2011,24(2): 201-204.

[14] 郭輝, 姬紅兵, 武斌. 采用擬蒙特卡羅法的被動多傳感器目標跟蹤[J]. 西安電子科技大學學報(自然科學版), 2010, 37(6):1042-1046.GUO Hui, JI Hongbing, WU Bin. Quasi-Monte Carlo Gaussian particle filter based target tracking for the multiple passive sensor[J]. Journal of Xidian University (Natural Science), 2010,37(6): 1042-1046.

[15] 羅付巖, 徐海云. 擬蒙特卡羅模擬方法在金融計算中的應用研究[J]. 數理統計與管理, 2008, 27(4): 605-609.LUO Fuyan, XU Haiyun. The applying of Quasi-Monte Carlo methods in financial computation[J]. Application of Statistics and Management, 2008, 27(4): 605-609.

[16] Antonov I A, Saleev V M. An economic method of computing LP-sequences[J]. USSR Comput Math Math Phys, 1979, 19:252-256.

[17] Tabesh M, Tanyimboh T T, Burrows R. Head driven simulation based reliability of water distribution network[J]. Journal of Water Resources Planning and Management, 2001, 127(4):206-209.