時間序列分析法在突發公共衛生事件網絡輿情分析中的應用研究*
山東濰坊醫學院(261053) 滕文杰
近年來,突發公共衛生事件頻繁發生,嚴重損害公眾生命健康,危及社會安全穩定。在突發公共衛生事件發生發展過程中,網民關注與傳播成為主要推進因素,往往迅速演化為網絡輿情,并引發和帶動社會輿情的升溫。由于突發公共衛生事件具有明顯的時間節點,網民的關注也隨著時間的推進而出現量的變化,由此引發的網絡輿情的變化可以看做一組時間序列資料。本研究運用時間序列分析中的ARIMA(p,d,q)模型[1](差分自回歸移動平均模型,autoregressive integrated moving average),對突發公共衛生事件網絡輿情網民關注度進行趨勢分析和預測,分析網絡輿情的傳播規律,提出針對性的應急策略。
資料與方法
1.研究對象
選取2011年以來發生的典型突發公共衛生事件作為研究對象,分析其網絡輿情的變化。事件的選擇參考了原國家衛生部發布的2012年中國衛生十大新聞[2]、中華醫學會公共衛生分會等機構評出的2011年~2012年十大公共衛生事件[3]等,遴選確定了11個典型事件:瘦肉精、染色饅頭、地溝油、皮革奶、蒙牛黃曲霉素、碘鹽防輻射、白酒塑化劑、毒膠囊、黃金大米、塵肺鄉、毒生姜。
2.數據來源
利用百度指數搜索指數(即用戶關注度)[4]收集數據。搜索指數反映了網民對相應關鍵詞在一定時期的關注度。搜索指數關注度指標能夠比較有效地反映突發事件網絡輿情的變化情況[5]。分別以11個典型事件作為關鍵詞,利用百度搜索指數,收集各事件在事件發生前一天開始、到事件發生后60天內的網絡關注度數據,構成11組時間序列資料。
3.研究方法
(1)構建平均數時間序列
為分析11組時間序列資料的發展規律,采用事件發生點作為統一的時間點,組成一一對應的數據點,分別取各對應點的均值,構成平均數時間序列。平均數時間序列能夠反映現象一般水平的發展變化過程和趨勢[6]。
(2)ARIMA(p,d,q)模型[1]
ARIMA(p,d,q)模型主要用于非平穩時間序列的隨機分析,實質上是差分運算和ARMA模型(自回歸移動平均模型,autoregressive moving average)的組合,p,q為自相關和移動平均階數,d為差分次數。任何非平穩序列只要通過適當階數的差分實現差分后平穩,就可以對差分后序列進行ARMA模型擬合。
ARIMA(p,d,q)模型建模主要包括以下步驟:對原始序列進行平穩性檢驗;對非平穩序列進行差分運算;對平穩d階差分序列進行白噪聲檢驗;對平穩非白噪聲差分序列擬合ARMA模型;對殘差序列進行檢驗。整個統計分析借助SAS軟件實現。
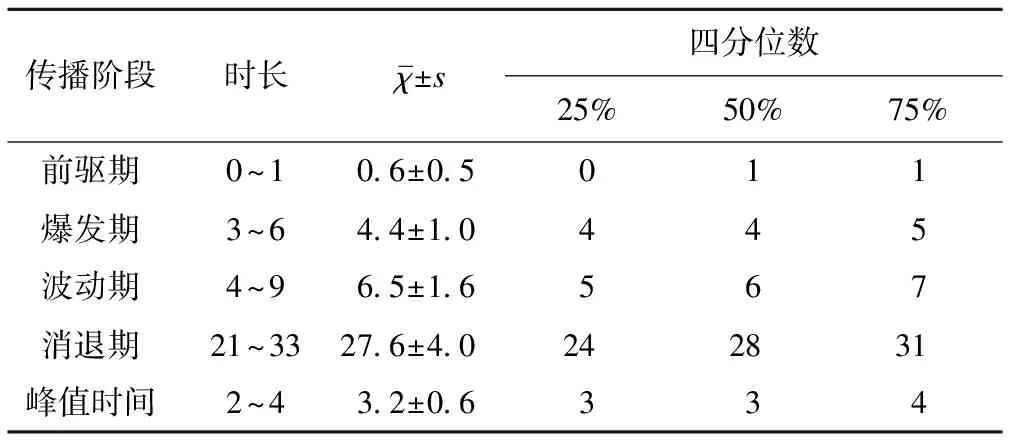
模型是指d階差分后自相關最高階數為p,移動平均最高階數為q的模型,通常包含p+q個獨立的未知系數:φ1,…,φp,θ1,…,θq。如果模型中有部分自相關系數φj(1≤j 根據11組原始時間序列數據,構建平均數時間序列做時序圖,顯示該序列有明顯遞減趨勢、無周期波動,為非平穩序列(圖1)。 圖1 突發公共衛生事件網絡輿情關注度時序圖 對原始序列進行1階差分,差分后序列在均值附近比較穩定地波動,沒有明顯趨勢,基本認為是平穩的。對平穩的一階差分序列進行白噪聲檢驗可以看出延遲6階和12階時,P值均<0.05,說明差分后序列不是純隨機序列,具有短期相關性,可以進行建模分析(見表1)。 表1 突發公共衛生事件網絡輿情關注度1階差分后序列白噪聲檢驗 考察1階差分后序列的自相關圖和偏自相關圖,由于隨機性影響并沒有呈現明顯的截尾性,因此采用最小信息準則BIC進行最優定階,從所有階數范圍內采用SAS程序MINIC定階命令進行最優定階。經分析,發現自回歸階數p=5時,移動平均階數為4時,BIC為最小(11.87294)。因此,嘗試構建ARIMA(5,1,4)模型。采用條件最小二乘法識別模型系數,進行參數顯著性檢驗發現,p=1,3,4,5,q=4時,參數都不顯著。p=2,q=1,2,3時,參數顯著。因此,需要建立一階差分自回歸移動平均疏系數模型即ARIMA((2),1,(1,2,3))。 用SAS軟件重新進行模型定階運算,構建一階差分自回歸移動平均疏系數模型即ARIMA((2),1,(1,2,3)),參數估計結果見表2,P值均<0.05。模型表達式為(1-0.4616B2)(1-B)xt=(1+0.69127B-0.81438B2-0.79934B3)εt。 表2 突發公共衛生事件網絡輿情關注度ARIMA((2),1,(1,2,3))參數估計結果 對模型進行殘差純隨機性檢驗,發現延遲6,12,18,24階時P值分別為0.1545,0.7884,0.9819,0.9995,均>0.05,也就是模型通過殘差自相關性檢驗,可以認為模型擬合效果良好。模型擬合效果見圖2。 圖2 突發公共衛生事件網絡輿情關注度ARIMA((2),1,(1,2,3))模型擬合效果圖 根據危機生命周期理論,突發性公共衛生危機通常遵循特定的生命周期,經典的是美國危機管理學家Steven Fink 1986年提出的四階段模型:前驅階段、急性階段、慢性階段、治愈階段[7]。根據這一理論,分析擬合曲線的轉折、降消特點,呈現明顯的上升、達到高峰,下降、反復波動,消退、低位震蕩、趨于穩定的特征,因此將突發公共衛生事件網絡輿情分為四個階段:前驅期、爆發期、波動期、消退期。前驅期指事件發生節點到網絡輿情急劇升溫前的折點;爆發期指網絡輿情出現第一個完整高峰的時長;波動期指輿情反彈、高位波動、表現第2峰或多峰的時長;消退期指持續下降、低位震蕩、趨于穩定的時長。網絡輿情的消退呈現一個長尾特性,而且網絡輿情關注度很難下降到發生前的水平。從網絡輿情的監控來講,將輿情下降到接近事件發生前的水平并趨于穩定作為消退期的終結。示意圖如圖3。 圖3 突發公共衛生事件網絡輿情傳播階段示意圖 根據傳播階段的劃分和11組突發公共衛生事件網絡輿情關注度原始數據時序圖,分別統計各階段的時長,用均值(反映集中趨勢)和四分位數(反映離散趨勢)表示11組數據總體傳播階段的變化情況。結果顯示,突發公共衛生事件網絡輿情前驅期很短,平均0.6天,有一半事件沒有前驅期,呈現急劇升溫現象;爆發期平均4.4天,多數為4天;波動期平均6.5天;消退期平均27.6天;到達峰值的時間平均3.2天,多數為3天(表3)。 表3 突發公共衛生事件網絡輿情傳播階段時長(天數) ARIMA模型是經典的時間序列分析方法,主要用于隨機平穩時間序列擬合建模和外推預測。由于ARIMA模型是對連貫的歷史數據的分析,數據量越大,模型越準確。差分運算是非平穩序列平穩化的主要途徑,差分階數的選擇主要依據原始序列的特定規律,識別線性趨勢、曲線趨勢、固定周期趨勢選擇合適的差分方式,但差分運算的階數要適當,避免過差分,而導致大量信息的損失。另外,疏系數模型的選擇,要在傳統定階方法的基礎上,進行反復嘗試,刪除不顯著的參數,逐步優化模型,構造疏系數模型。本例中,突發公共衛生事件網絡輿情作為時間序列的大數據資料,ARIMA模型能夠得到很好的應用,擬合效果較好。 根據突發公共衛生事件網絡輿情的傳播規律,危機應對應把握以下幾點:①前驅期很短,事件發生第一天是輿情應對的“黃金期”。應對時間越早、措施越得當、聲音越及時,影響越小,整個周期越短。②高峰期是網絡輿情監控和應對的關鍵期,呈現“4天規律”。在高峰期的上升期,即事件發生的第2、3天,是危機應對的“第一關鍵期”,處理及時,應對得當,可以使輿情產生“拐點”,降低峰值,縮短時長。在高峰期的下降期,即事件發生的第4、5天,是危機應對的“第二個關鍵期”,處理得當,可以迅速降低輿情熱度,縮短波動期時長,甚至可以阻止波動期出現,直接進入消退期。③波動期表現為輿情的反復,是危機應對的“強化期”,相關處理措施應及時跟進,盡快推進輿情進入消退期。④前三個階段是危機應對的重點階段,總體呈現“10天規律”,應把握關鍵環節,綜合應對,主導網絡話語權,引導事件和輿情發展方向。但應注意,網絡輿情的四階段傳播,僅是一般規律的反映,會受到危機應對等因素的影響,可能帶來某一階段時長的縮短甚至消除,應根據特定事件具體分析。 參 考 文 獻 1.王燕.應用時間序列分析.北京:中國人民大學出版社,2008:146. 2.國家衛生計生委.2012年中國衛生十大新聞[EB/OL].(2013-01-10)[2014-3-20].http://www.moh.gov.cn/wsb/pxwfb/201301/d184d25bce2040abb9553606e658fd2c.shtml. 3.人民網.2011-2012年公共衛生十大新聞熱點[EB/OL].(2012-05-11)[2014-3-20].http://medicine.people.com.cn/GB/135395/17860890.html. 4.百度.百度搜索指數[EB/OL].[2014-3-20].http://index.baidu.com/Helper/?tpl=help&word=%CA%DD%C8%E2%BE%AB. 5.陳濤,林杰.基于搜索引擎關注度的網絡輿情時空演化比較分析-以谷歌趨勢和百度指數比較為例.情報雜志,2013,32(3):7-10. 6.楊國良.統計學原理.第1版.重慶:重慶大學出版社,2006:159. 7.葉金珠.網絡突發事件蔓延及干預研究.武漢:華中科技大學,2012:40.結果與分析
1.原始序列時序圖
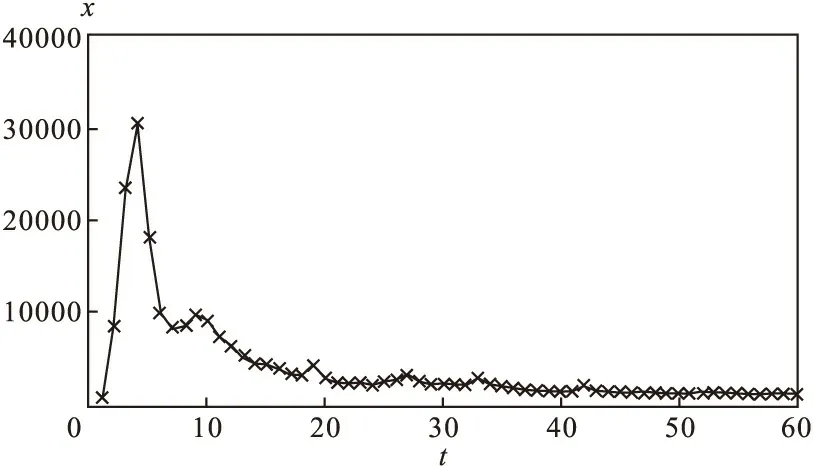
2.差分運算及白噪聲檢驗

3.相對最優定階及模型建立
4.構建疏系數模型ARIMA((2),1,(1,2,3))
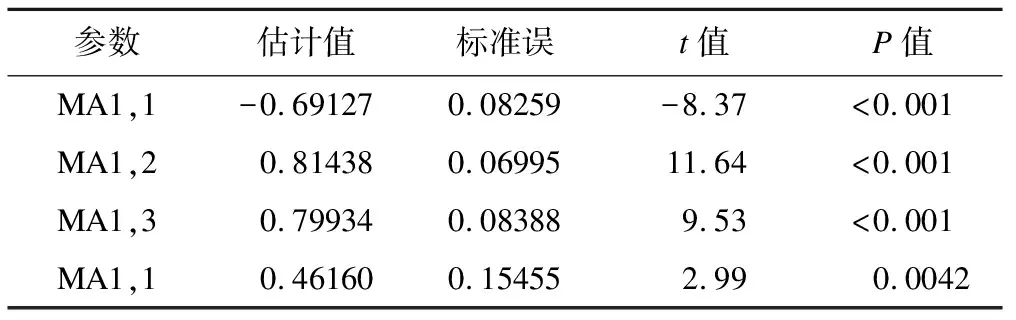
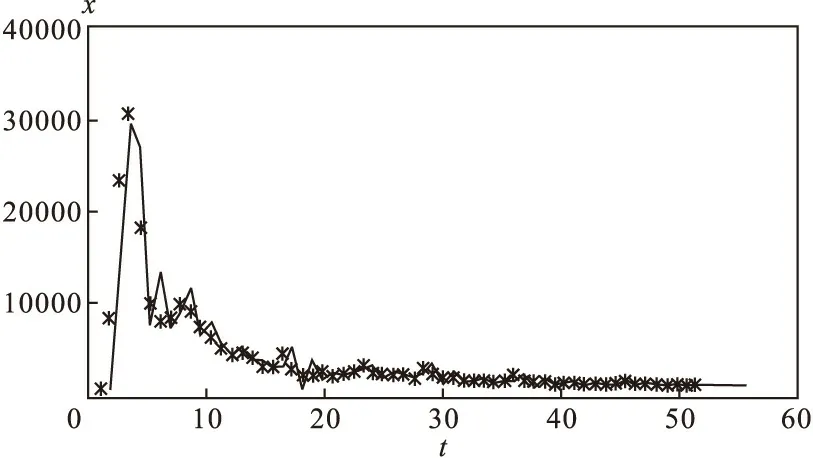
5.網絡輿情傳播規律分析
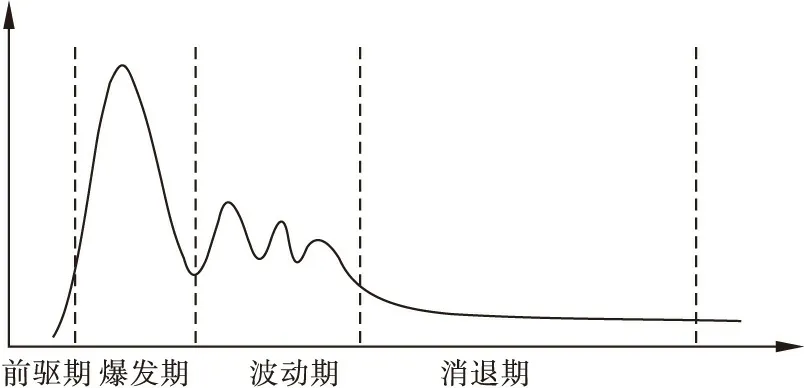
6.網絡輿情傳播階段的時長分析
討論與建議
1.ARIMA模型的應用
2.突發公共衛生事件網絡輿情的應急策略

