基于NSCT-GLCM的CT圖像特征提取算法

張人上

ZHANG Renshang

山西財經大學 信息管理學院，太原 030006

Faculty of Information Management,Shanxi University of Finance and Economics,Taiyuan 030006,China

隨著各種影像檢查技術成熟，醫院收集了海量的CT圖像影，如何對這些圖像進行挖掘，幫助醫生診斷病例具有十分重要的意義。圖像分割是采用CT圖像進行心臟疾病診斷的基礎，因此提高CT圖像分割準確率已成為一個重要的研究課題[1-2]。

實際CT圖像分割實際是一種多分類問題，CT圖像特征提取是基礎和關鍵[3-4]。CT圖像的紋理信息非常豐富，灰度共生矩陣（Gray Level Co-occurrence Matrix，GLCM）是描述紋理的常用方法，但其對紋理特征的描述不夠細致，致使其用于特征提取不夠好[5-6]。很多學者利用小波變換的多分辨優點，與GLCM相結合提取CT圖像的紋理特征，如：周平提出基于小波變換的共生特征提取方法，但忽略了對小波變換細節子帶的利用[7]；韓彥芳提出在小波細節子帶中使用GLCM提取紋理共生特征，但僅用小波細節子帶不足以描述不同的紋理細節[8]；付增良等人提出7個共生特征的CT圖像分割方法[9]。采樣輪廓變換（Non-Subsampled Contourlet Transform，NSCT）作為一種多尺度幾何分析工具，具有對曲線奇異性函數的最優表示形式，可克服小波變換的上述不足[10]。為此，有學者等提出一種NSCT和支持向量機（Support Vector Machine，SVM）相融合的圖像分割算法，但僅提取圖像的多尺度紋理特征，而忽略了紋理的空間結構信息[11]。

為了提高CT圖像的分割準確率，提出一種NSCT和GLCM相融合的CT圖像特征提取算法（NSCT-GLCM），并采用SVM實現圖像分割，最后通過仿真實驗驗證了算法的有效性。

1 提取CT圖像的特征

1.1 非下采樣輪廓變換

非下采樣輪廓變換（NSCT）包括金字塔濾波器組（NSPFB）和方向濾波器組（NSDFB）兩部分，結構原理如圖1所示[12]。NSCT分解過程為：首先利用NSPFB對圖像進行多尺度的分解，得到各種不同頻率的高頻子帶圖像和一個低頻子帶圖像，然后利用NSDFB對得到的各高頻子帶圖像進行多方向分解，從而得到不同尺度、不同方向的子帶圖像。

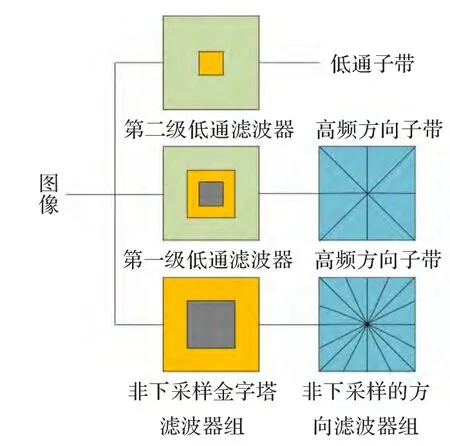
圖1 NSCT的工作原理圖

1.2 灰度共生矩陣

從灰度值為i的像素點出發，直線距離為d，角度為θ的另一個像素點的灰度值為 j，兩個灰度值在整個圖像中同時發生的概率為：

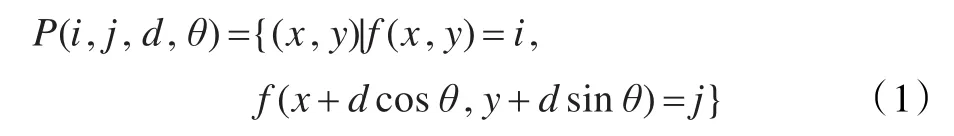
常用的CT圖像紋理特征為同質區（HOM）、角二階矩（ASM）、熵（ENT）和非相似性（DIS），它們定義如下：

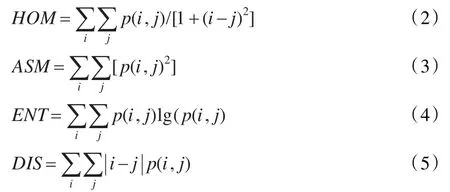
1.3 NSCT-GLMC提取紋理特征

設輸入CT圖像為 f(x，y)，大小為 M×N，NSCT分解的過程可以表示為：

式中，bj，k為 j尺度、k方向的高頻子帶；αJ為低頻子帶。

基于NSCT-GLCM特征提取步驟如下：

（1）圖像的NSCT分解。先用NSCT將圖像進行2層分解，第一尺度方向數為8，第二尺度方向數為4，這樣圖像就分解為具有不同尺度、不同方向的子帶，共得到13個和原圖大小均相同的子帶，每個方向子帶代表一個方向的紋理。

（2）變換系數量化。NSCT低頻子帶αJ近似服從均勻分布，而高頻子帶則呈現出“高尖峰、長拖尾”的分布，對低頻子帶采用均勻量化，量化級為16，即按公式（7）量化，其中，[]表示向下取整。

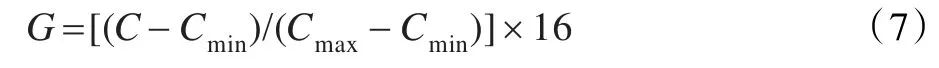
對細節子帶采用非均勻量化，將系數量化為16級，先估計同一尺度的各個子帶方差σl，量化時以 ±3σ為界限，按式（8）進行分段量化：

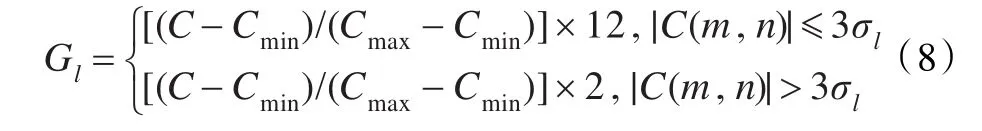
（3）窗口的選取，包括窗口遍歷方式和窗口大小選取。GLCM的窗口遍歷圖像方式采用重疊窗口，對不同NSCT分解尺度下使用大小不同的窗口。對第一尺度的子帶圖像使用N=3×3大小的窗口，第二尺度的子帶圖像和低頻子帶使用N=5×5大小的窗口。

（4）距離參數d。隨著NSCT分解參數設置的不同，變換方向數將變化，尺度間的差異隨著方向參數的變化存在一定的差異，因此對NSCT分解子帶求灰度共生量時，對不同尺度采用不同距離間隔d。

（5）方向 θ 選取。通過GLCM公式（2）～（5）提取共生量，對NSCT各個子帶計算4個角度（即角度θ分別取0°，45°，90°，135°）的HOM、ASM、ENT、DIS這四個共生量，然后對得到每個共生量的四個不同方向的值取平均值，如式（9）所示，以此來提高灰度共生量對方向的魯棒性。

最后得到圖像點(m，n)的52維共生特征量：

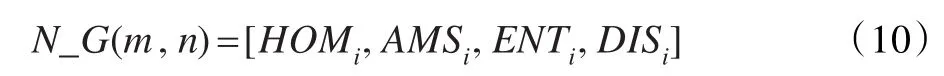
2 支持向量機的CT圖像分割

CT的圖像分割實際是一種分類問題。假設樣本集為{xi，yi}，i=1，2，…，n，xi∈Rd，d 是訓練樣本的維數，n是訓練樣本規模，yi為類別標號，SVM使得對線性可分的樣本集滿足：

引入Lagrange乘子將上述最優分類面問題轉化為對偶問題，相應的約束條件為：

對αi求解下列函數的最大值：

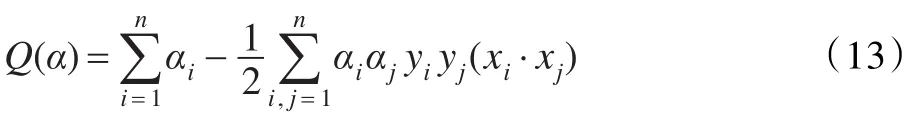
式中，αi為Lagrange乘子[13]。

若αi為最優解，那么有：

最優分類面的權系數向量就是訓練樣本向量的線性組合，解中只有很少的一部分αi不為零，對應的樣本即為支持向量。

求解上述問題后得到的最優分類函數為：

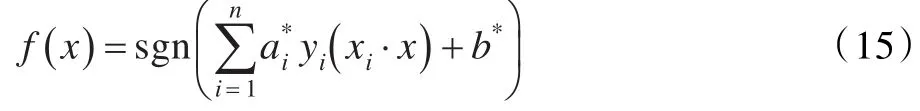
為了減少泛化誤差，引入非負的松弛變量ξi來對式（11）的條件進行放寬，約束條件變為：

引入錯誤懲罰分量，目標函數為：

式中，C為懲罰因子。

不同的核函數會生成不同形式的SVM，由于徑向基核函數（RBF）只需確定一個參數（即核函數寬度參數σ），有利于參數優化，因此，研究選擇RBF核函數構造SVM。RBF核函數定義如下：

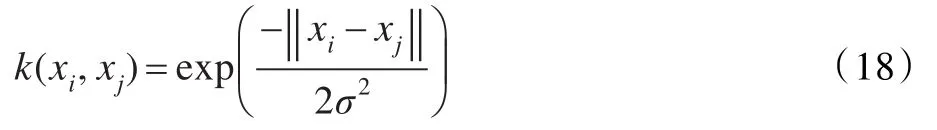
3 仿真實驗結果

3.1 實驗環境

為了驗證NSCT-GLCM算法的性能，在Windows 7操作系統，Pentium?Dual-Core E6300@2.80 GHzCPU，4 GB RAM平臺，并采用Matlab 2013編程實現仿真實驗。NSCT-GLCM算法的塔式濾波器組選用“dmaxflat7”，采用二層分解，得到1個低頻子帶和12個高頻子帶；方向濾波器組選用“maxflat”，分解層數為[23]，所提取的特征包括NSCT-GLCM算法提取ASM、HOM、ENT、DIS共52維紋理特征量。

3.2 特征向量的歸一化

原始特征分量變化區間很大，不利于后續特征向量的分類，因此在使用SVM進行CT圖像分類之前，對特征向量進行歸一化處理，具體為：

式中，Fi是歸一化前的第i個特征分量值；fi是歸一化后的第i個特征分量；Fimax和Fimin分別為第i個特征分量的最大值和最小值。

3.3 結果與分析

3.3.1 單一紋理特征的圖像分割性能分析

圖2為一幅去噪后的CT圖像，首先采用NSCT-GLCM算法提取CT圖像的紋理特征，由于粗糙紋理（高頻子帶）用較小的距離，平滑紋理（低頻子帶）用較大的距離。以此為依據，本文第一層變換8個子帶的距離采用d=1，第二層變換4個子帶和低頻子帶的距離采用d=2，然后SVM分別HOM、ASM、ENT、DIS這四種紋理特征進行分割，單特征CT分割結果見圖3（a）～（d）。

圖2 去噪后的CT圖像

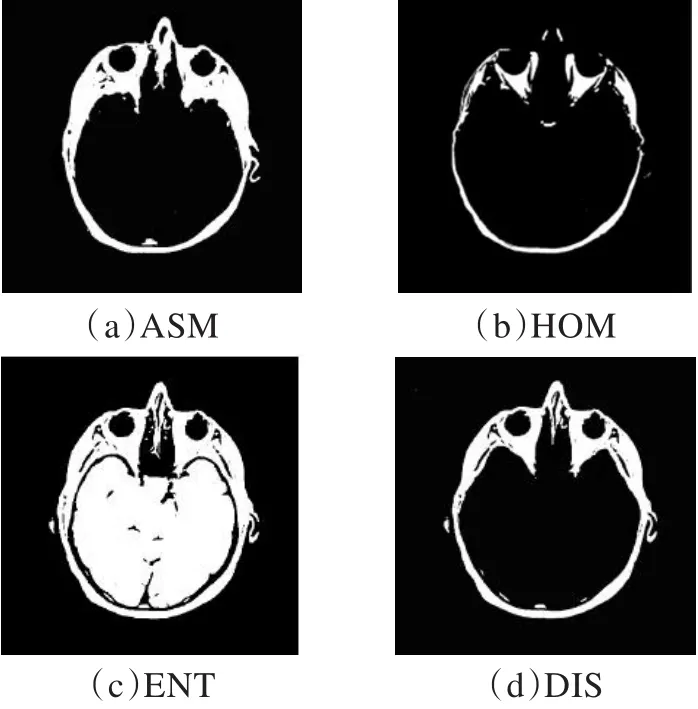
圖3 單一紋理特征的分割圖

從圖3可知，分割結果圖的許多區域出現了過分割和欠分割的現象，因此采用單一紋理特征難以獲得比較理想的CT圖像分割結果。

從圖 3（a）～（d）可看出，圖 3（a）、（c）、（d）非常相似，即這三個特征量（ASM、ENT、DIS）存在較強的相關性，若對它們進行特征選擇，從原始特征向量中去除相關性較強的特征量，保留有互補性的、對后續分割更為有效的特征，就可以去除冗余特征，降低維數，減小計算量，提高CT圖像的分割效率和分割精度。兩幅圖像相關性大小的計算公式為：

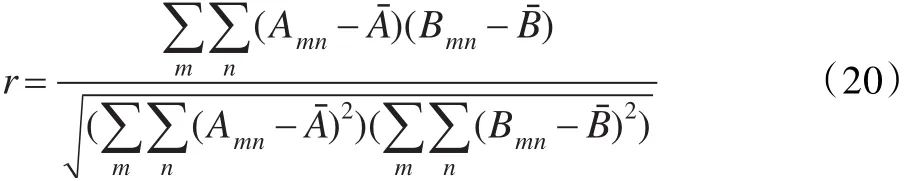
式中，mean()表示取矩陣均值；Aˉ=mean2(A)；Bˉ=mean2(B)。

將上面四個共生統計量分別在同一尺度上、同一方向對應的13個子帶中計算兩兩之間相關系數的絕對值，并對13個子帶計算結果進行平均，相關系數見表1。

表1 統計量間的相關系數

從表1可知，HOM與ASM的相關系數小于0.5，與ENT和DIS相關系數大于0.6，與DIS之間高度相關；ASM與ENT和DIS的相關系數也大于0.6；DIS則與HOM、ASM、ENT都有較高的相關性，都大于0.6，因此采用主成分分析（Principal Component Analysis，PCA）對52維特征維數進行維降處理，選擇對CT圖像分割貢獻最大的特征。

3.3.2 與WA-GLCM算法的性能對比

為了驗證NSCT-GLCM算法的優越性，采用小波域（WA）的GLCM特征提取算法（WA-GLCM）作為對比算法，小波基選用“db1”，采用二層分解，得到一個低頻子帶和6個高頻子帶，WA-GLCM算法提取特征為小波域的HOM、ASM、ENT、DIS共52維紋理特征量，并采用PCA進行降維處理。實驗中采用圖像為圖2中的CT圖像；圖4為對應的專家分割圖，用于計算分割準確率和目測分割效果的參照模板。圖5為兩種特征提取方法的分割結果圖；其中圖5（a）和（b）分別為WA-GLCM算法和NSCT-GLCM算法的分割結果。

圖4 專家分割圖

圖5 兩種特征提取方法的分割結果圖

對圖 5（a）、（b）分割結果進行對比分析可知，WA-GLCM的分割結果出現明顯的欠分割，在圖像的細節處未能將其分割出來，存在較嚴重的誤分，所得的邊緣不夠平滑，邊界信息丟失嚴重。相比而言，NSCT-GLCM能較好地將目標分割出來，分割的目標也更有連續性，所得的圖像邊緣更加清晰平滑，分割結果邊緣與原始圖像邊緣吻合較好。對比實驗的分割結果圖表明，NSCT-GLCM算法能較好保持圖像邊緣細節信息，可以檢測到CT圖像中更多的邊界，保留更細小的細節。

同時將上述實驗結果與人工分割結果比較，并計算分割準確率，分割準確率定義如下：

將圖5（a）、（b）分別與圖4進行比較計算，分割準確率如表2所示。從表2可知，NSCT-GLCM算法的分割準確率要比WA-GLCM高0.0174，這說明NSCT-GLCM算法可以獲得比WA-GLCM更優的特征，可以有效地減少像素錯分，從而達到了較為滿意的分割效果。

表2 兩種特征提取算法的分割準確率

3.3.3 與經典CT圖像分割性能對比

為了進一步說明NSCT-GLCM算法的優越性，采用與文獻[14]的經典CT圖像分割算法進行對比實驗。圖7（a）和（b）分別為文獻[14]和NSCT-GLCM算法的分割結果圖。對比圖7（a）、（b）可知，相對于對比算法，NSCTGLCM算法所得的圖像邊緣更加清晰平滑，分割結果邊緣與原始圖像邊緣吻合得更好。

圖6 原始CT圖像

圖7 NSCT-GLCM與文獻[14]的分割結果對比圖

綜合上述可知，NSCT-GLCM算法可以獲得較優的CT圖像特征，可減少像素的錯分，并得到更好的邊緣保持效果，所得的分割圖像和原始CT圖像的吻合度高。

4 結束語

CT特征提取是CT圖像分割的基礎和關鍵，而CT圖像的特殊性使得一般的圖像分割方法往往失效，為了提高CT圖像分割精度，提出一種基于NSCT-GLMC的CT圖像特征提取方法，并采用SVM建立分類器實現圖像分割。實驗結果表明，NSCT-GLMC可以獲得到更為精細而平滑的邊界方向信息，能夠有效地消除區域內的像素錯分，得到較精準的CT圖像分割結果。

[1]Karthikeyan C，Ramadoss B，Baskar S.Segmentation algorithm for CT images using morphological operation and artificial neural network[J].International Journal of Signal Processing，ImageProcessing and Pattern Recognition，2012，5（2）：115-122.

[2]郭華磊，馬苗.改進的模糊C均值聚類的圖像分割算法[J].計算機工程與應用，2011，47（1）：176-178.

[3]魯昌華，盛柳青，岳公和.基于MRF模型的NSCT域SAR圖像分割[J].計算機工程與應用，2013，49（16）：172-174.

[4]Heimann T，van Ginneken B，Styner M A，et al.Comparison and evaluation of methods for liver segmentation from CT datasets[J].IEEE Transactions on Medical Imaging，2009，28（8）：1251-1265.

[5]商艷麗.基于形態學重構運算的醫學CT圖像濾波方法[J].中國體視學與圖像分析，2011，16（1）：103-107.

[6]周平，李傳富，符志鵬.基于小波分解的腦CT圖像紋理特征提取[J].儀器儀表學報，2010，31（3）：643-648.

[7]韓彥芳，施鵬飛.基于多層小波和共生矩陣的紋理表面缺損檢測[J].上海交通大學學報，2006，40（3）：425-430.

[8]付增良，陳曉軍，葉銘，等.心臟CT圖像分割方法[J].計算機工程，2009，35（12）：189-191.

[9]趙一凡，夏良正.基于輪廓波特征的紋理圖像識別方法[J].東南大學學報：自然科學版，2008，38（2）.

[10]劉露，楚春雨，馬建為，等.支持向量機與區域增長相結合的CT圖像并行分割[J].計算機科學，2010，37（5）：237-240.

[11]汪國強，曲晶瑩.改進分水嶺醫學圖像分割方法的研究[J].計算機工程與應用，2013，49（8）：185-187.

[12]鐘樺，楊曉鳴，焦李成.基于多分辨共生矩陣的紋理圖像分類[J].計算機研究與發展，2011，48（11）：1991-1999.

[13]賀元元，張雪英，劉曉峰.多類分類預選取的SVM在語音識別中的應用[J].計算機工程與應用，2013，49（7）：115-118.

[14]蔣冬梅，張建州，閆超.CT圖像椎骨分割的局部模糊主動輪廓方法[J].計算機工程與應用，2013，49（15）：201-203.

[15]Do M N，Vetterli M.The contourlet transform：an efficient directional multiresolution image representation[J].IEEE Transon ImageProcessing，2005，14（12）：2091-2106.